陕西省澄城县2022届下学期九年级中考模拟考试数学试卷（二模）

试卷更新日期：2022-05-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $3^{- 1} \times 3$ 的结果为（）

A、1 B、3 C、 $- \frac{1}{3}$ D、 $- 1$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 太阳与地球的平均距离大约是150 000 000千米，数据150 000 000用科学记数法表示为（）

A、1.5×10⁸ B、1.5×10⁹ C、0.15×10⁹ D、15×10⁷

查看试题解析
4. 如图所示，已知直线 $A B$ ， $C D$ 相交于点O， $O A$ 平分 $∠ E O C$ ， $∠ E O C = 100 °$ ，则 $∠ B O D$ 的度数是（）

A、 $20 °$ B、 $40 °$ C、 $50 °$ D、 $80 °$

查看试题解析
5. 在同一平面直角坐标系中，直线 $y = k x - 3$ 是由直线 $y = 2 x + b$ 经过平移得到的，则下列各点在直线 $y = k x - 3$ 上的是（）

A、 $(- 2 ， 1)$ B、 $(1 ， - 2)$ C、 $(3 ， 3)$ D、 $(5 ， 13)$

查看试题解析
6. 如图，在正方形ABCD的外侧作等边 $△ C D E$ ，对角线AC与BD相交于点O，连接AE交BD于点F，若 $O F = 1$ ，则AB的长度为（）

A、2 B、 $\sqrt{6}$ C、 $2 \sqrt{2}$ D、3

查看试题解析
7. 二次函数 $y = (x - 1) (x - a)$ （a为常数）图象的对称轴为直线 $x = 2$ ，将该二次函数的图象沿y轴向下平移k个单位，使其经过点 $(0 ， - 1)$ ，则k的值为（）

A、3 B、4 C、2 D、6

查看试题解析

二、填空题

8. 将实数2， $- 1$ ，0， $- \sqrt{5}$ 从小到大用符号“<”连接起来.

查看试题解析
9. 若n边形内角和是外角和的3倍，则n=.

查看试题解析
10. 如图所示，南宋数学家杨辉在《解：九章算法》中出现的三角形状的数阵，又称为“杨辉三角形”，该三角形中的数据排列有着一定的规律，根据图中的数构成的规律，a所表示的数是.

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，过点 $D$ 作 $D E ⊥ A B$ 于 $E$ ，若 $B E = 3$ ， $△ B D E$ 的周长为11，则 $B C =$ ．

查看试题解析
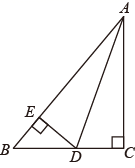12. 已知一个反比例函数的图象与正比例函数 $y = 4 x$ 的图象无交点，请写出一个满足上述条件的反比例函数的表达式.（只写一个即可）

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A D = 2 A B = 4$ ，点E是 $A D$ 上一点， $D E = 1$ ，F是 $B C$ 上一动点，P、Q分别是 $E F$ ， $A E$ 的中点，则 $P E + P Q$ 的最小值为.

查看试题解析

三、解答题

14. 计算： $(\sqrt{6} + 2) \div \sqrt{2} + | \sqrt{3} - 4 | - {(- 2)}^{2}$ .

查看试题解析
15. 化简： $(x + y) (x - y) - (4 x y - 8 x y) \div 2 x y$ .

查看试题解析
16. 解不等式组： ${\begin{cases} \frac{3 x - 2}{3} \geq 1 ， \\ 4 x - 5 < 3 x + 2 ， \end{cases}$ 并写出不等式组的最小整数解.

查看试题解析
17. 如图，已知 $△ A B C$ ，利用尺规以点A为圆心作 $⊙ A$ ，使 $⊙ A$ 与 $B C$ 相切.（不写作法，保留作图痕迹）

查看试题解析
18. 解分式方程： $\frac{1}{x - 3} + \frac{2 x - 1}{x + 3} = 2$ .

查看试题解析
19. 如图，在矩形 $A B C D$ 中，点E，F分别是 $A D$ ， $A B$ 上的点， $E F ⊥ E C$ ，且 $A E = C D$ .求证： $A F = D E$ .

查看试题解析
20. 汉中盆地是油菜花的故乡，每年花开时节，犹如一片黄色海洋，百万亩油菜花同时怒放，是中国最秀美的山水风光之一.据了解，汉中某地去年种植油菜2万亩，并计划种植油菜亩数逐年增加，预计明年种植油菜2.42万亩，求该地这两年种植油菜亩数的年平均增长率.

查看试题解析
21. 中国空间站作为国家太空实验室，也是重要的太空科普教育基地，对激发社会大众特别是青少年弘扬科学精神、热爱航天事业具有特殊优势.“天宫课堂”第二课已于2022年3月23日下午开讲并直播.航天员相互配合，生动演示了微重力环境下A.太空“冰雪”实验、B.液桥演示实验、C.水油分离实验、D.太空抛物实验.某班的班主任为加深同学们的印象，让每位同学各自从这四个实验中随机抽取一个，制作手抄报讲解实验现象背后的科学原理.

(1)、求该班班长随机抽取的实验是“太空抛物实验”的概率；

(2)、小丽和小雨也是该班同学，利用树状图或列表的方法求小丽和小雨抽到不同实验的概率.

查看试题解析
22. 榆林中心广场雕塑“世纪争辉”表现了榆林人民热情开放，团结进取的奋进精神.小明利用无人机测量该雕塑的高 $A B$ ，如图，无人机在空中C处观测到雕塑顶端A的仰角为42°，雕塑底部B的俯角为31°，此时无人机距地面的距离 $C D = 7.2$ 米，已知 $A B ⊥ B D$ ，求雕塑的高度 $A B$ .（参考数据： $\tan 31 ° = 0.6$ ， $\tan 42 ° = 0.9$ ）

查看试题解析
23. “双减”政策的出台，为阅读活动的有效开展提供了广阔空间和有利契机.阅读素养是学生全面发展的重要基础素养，阅读是学生终身成长的重要路径.某校为了解学生课外阅读情况，校委会就“你阅读了几本课外书？”这一问题在全校范围内进行了调查，并随机抽取部分调查结果，将各类的人数绘制成如图的扇形图和条形图.

请根据图中信息，解答下列问题：

(1)、扇形图中m的值为；

(2)、求本次调查所抽取的样本数据的众数、中位数、平均数；

(3)、若该校有1500名学生，请你估计其中阅读了8本课外书的学生共有多少名？

查看试题解析
24. 张伯伯家专业种植狗头枣，他利用直播销售方式把狗头枣远销全国各地.对狗头枣出售价格根据购买量给予优惠，设顾客一次性购买狗头枣 $x kg$ ，付款y元，y与x之间的函数关系如图所示.

(1)、求y与x之间的函数关系式；

(2)、某位顾客通过直播在张伯伯家一次性购买狗头枣共花费870元，这位顾客共购买了多少千克狗头枣？

查看试题解析
25. 如图，在 $△ A B C$ 中，点E是 $B C$ 的中点，连接 $A E$ ，以 $A B$ 为直径作 $⊙ O$ ， $⊙ O$ 交 $B E$ 于点D， $A C$ 为 $⊙ O$ 的切线.

(1)、求证： $∠ A E B = 2 ∠ C$ ；

(2)、若 $A C = 8$ ， $\sin B = \frac{4}{5}$ ，求 $D E$ 的长.

查看试题解析
26. 如图，抛物线 $y = a x^{2} + b x$ 经过坐标原点O与点 $A (3 ， 0)$ ，正比例函数 $y = k x$ 与抛物线交于点 $B (\frac{7}{2} ， \frac{7}{4})$ .

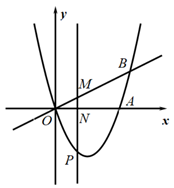(1)、求该抛物线的函数表达式；

(2)、点P是第四象限抛物线上的一个动点，过点P作 $P M ⊥ x$ 轴于点N，交 $O B$ 于点M，是否存在点P，使得 $△ O M N$ 与以点N、A、P为顶点的三角形相似？若存在，请求出点P的坐标；若不存在，请说明理由.

查看试题解析
27.

(1)、问题提出
如图①，在矩形 $A B C D$ 中，点E为 $A B$ 上一点， $A E = 3$ ，在 $C D$ 上有一点F，连接 $E F$ ， $E F$ 将矩形 $A B C D$ 的面积平分，则 $C F$ 的长为；

(2)、问题探究
如图②，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $∠ A = 60 °$ ， $A B = 10$ ，点E是 $A B$ 上一点， $B E = 2$ ，点F是射线 $B C$ 上一动点， $△ B E F$ 与 $△ M E F$ 关于 $E F$ 对称，求点M到 $A C$ 距离的最小值；

(3)、问题解决
如图③，某公园计划建一个形状为 $▱ A B C D$ 的游乐场，其中 $C D = 60$ 米， $B C = 100$ 米，连接 $A C$ ， $A C ⊥ A B$ .为方便工作人员通过，要留出一条快速通道 $E F$ ， $E$ 、 $F$ 是 $▱ A B C D$ 边上的动点（可与顶点重合），根据设计要求，线段 $E F$ 平分 $▱ A B C D$ 的面积，过点C作 $C P ⊥ E F$ 于点P，要将 $△ A D P$ 区域修建为家长休息等待区，为使游乐场容纳更多的游乐设施，要求家长休息等待区（即 $△ A D P$ ）的面积尽可能地小，问 $△ A D P$ 的面积是否存在最小值？若存在，请求出 $△ A D P$ 的最小面积；若不存在，请说明理由.

查看试题解析