陕西省宝鸡市岐山县2022届九年级上学期期中数学试卷（一模）

试卷更新日期：2022-05-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（　　）

A、3x²+ $\frac{1}{x}$ =0 B、2x﹣3y+1=0 C、（x﹣3）（x﹣2）=x² D、（3x﹣1）（3x+1）=3

查看试题解析
2. 顺次连接矩形各边中点得到的四边形是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
3. 一个不透明的袋中装有除颜色外均相同的 $2$ 个红球、 $1$ 个白球，从中随机摸出 $2$ 个球，则下列说法正确的是（）

A、至少有一个是白球 B、至少有一个是红球 C、一定是一个白球、一个红球 D、一定是两个红球

查看试题解析
4. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）

A、当AB＝BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当∠ABC＝90°时，它是矩形 D、当AC＝BD时，它是正方形

查看试题解析
5. 用配方法解一元二次方程 $x^{2} - 6 x - 5 = 0$ ，下列变形正确的是（）

A、 ${(x - 6)}^{2} = - 5 + 36$ B、 ${(x - 6)}^{2} = 5 + 36$ C、 ${(x - 3)}^{2} = - 5 + 9$ D、 ${(x - 3)}^{2} = 5 + 9$

查看试题解析
6. 在“抛一枚均匀硬币”的实验中，如果现在没有硬币，则下面各个实验中不能代替此实验的是（）

A、两个形状大小完全相同，颜色为一红一白的两个乒乓球 B、扔一枚图钉 C、人数均等的男生、女生，以抽签的方式随机抽取一人是男生或女生 D、两张扑克，“方块”代替“正面”，“梅花”代替“反面”

查看试题解析
7. 如图，将长方形纸片折叠，使A点落在边 $B C$ 上的F处，折痕为 $B E$ ，若沿 $E F$ 剪下，则折叠部分展开是一个正方形，其数学原理是（）

A、有一组邻边相等的矩形是正方形 B、对角线相等的菱形是正方形 C、两个全等的直角三角形构成正方形 D、轴对称图形是正方形

查看试题解析
8. 共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多440辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（）

A、1000（1+x）²=1000+440 B、1000（1+x）²=440 C、440（1+x）²=1000 D、1000（1+2x）=1000+440

查看试题解析

二、填空题

9. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - 4 x + 2 = 0$ 的两个实数根，则 $x_{1} + x_{2} =$ .

查看试题解析
10. 小华抛一枚质地均匀的硬币，连续抛五次，硬币落地均正面朝上，如果第六次抛硬币，那么硬币正面朝上的概率为.

查看试题解析
11. 如图，正方形 $A B C D$ ，延长 $A B$ 至E，使 $A E = B D$ ，则 $∠ B C E$ 的度数.

查看试题解析
12. 在分别写有数字 $- 1$ ， $0$ ， $2$ ， $3$ 的四张卡片中随机抽取一张，放回后再抽取一张，如果以第一次抽取的数字作为横坐标，第二次抽取的数字作为纵坐标，那么所得点落在第一象限的概率为.

查看试题解析
13. 如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，点P为BC边上一动点，PE⊥AB于点E，PF⊥AC于点F，连结EF，点M为EF的中点，则AM的最小值为．　

查看试题解析

三、解答题

14. 我们已经学习了一元二次方程的四种解法：因式分解法，开平方法，配方法和公式法．请从以下一元二次方程中任选一个，并选择你认为适当的方法解这个方程．
① $x^{2} - 3 x + 1 = 0$ ；② ${(x - 1)}^{2} = 3$ ；③ $x^{2} - 3 x = 0$ ；④ $x^{2} - 2 x = 4$ ．

查看试题解析
15. 如图，一条直线上有两只蚂蚁，甲蚂蚁在点A处，乙蚂蚁在点B处，假设两只蚂蚁同时出发，爬行方向只能沿直线AB在“向左”或“向右”中随机选择，并且甲蚂蚁爬行的速度比乙蚂蚁快.

(1)、甲蚂蚁选择“向左”爬行的概率为；

(2)、利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.

查看试题解析
16. 如图， $Δ A B C$ 是一块直角三角形余料， $∠ C = 90^{°}$ ，工人师傅要把它加工成一个正方形零件，使C成为正方形的一个顶点，其余3个顶点分别在 $A B ， A C ， B C$ 的边上，请你协助工人师傅用尺规画出裁割线.（用圆规、直尺作图，不写作法，保留作图痕迹.）

查看试题解析
17. 已知关于x的方程 $x^{2} - 2 (m + 1) x + m^{2} = 0$

(1)、当m取何值时，方程有两个实数根；

(2)、为m选取一个合适的整数，使方程有两个不相等的实数根，并求出这两个实数根.

查看试题解析
18. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
59
96
116
290
480
601
摸到白球的频率 $\frac{m}{n}$
　
0.64
0.58
　
0.60
0.601

(1)、完成上表

(2)、“摸到白球”的概率的估计值是　（精确到0.1）；

(3)、试估算口袋中黑、白两种颜色的球各有多少只？

查看试题解析
19. 如图所示， $DE$ 是 $ABCD$ 的 $∠ ADC$ 的平分线， $EF / / AD$ ，交 $DC$ 于F.

(1)、求证：四边形 $AEFD$ 是菱形；

(2)、如果 $∠ A = 60^{\circ}$ ， $AD = 5$ ，求菱形 $AEFD$ 的面积.

查看试题解析
20. 一个不透明的口袋里装有分别标有汉字“书”、“香”、“校”、“园”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀.

(1)、小明和小军做摸球游戏，若从中任摸一个球，球上的汉字刚好是“书”，则小明胜，否则小军胜，这个游戏对双方（填“公平”或“不公平”）；

(2)、从中任摸一球，不放回，再从中任摸一球，请用树状图或列表的方法，求摸出的两个球上的汉字能组成“书香”的概率.

查看试题解析
21. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ，D是的 $B C$ 边的中点， $D E ⊥ A C$ ， $D F ⊥ A B$ ，垂足
分别是E、F.

(1)、求证： $D E = D F$ ；

(2)、只添加一个条件，使四边形 $E D F A$ 是正方形，并给出证明.

查看试题解析
22. $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 5 cm$ ， $B C = 6 cm$ ，点P从点A开始沿边 $A B$ 向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边 $B C$ 向终点C以2cm/s的速度移动.如果点P、Q分别从点A、B同时出发，当点Q运动到点C时，两点停止运动.设运动时间为t秒.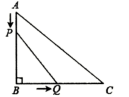

(1)、填空： $B Q =$ ， $P B =$ （用含t的代数式表示）；

(2)、是否存在t的值，使得 $△ P B Q$ 的面积等于 $4 {cm}^{2}$ ？若存在，请求出此时t的值；若不存在，请说明理由.

查看试题解析
23. 有两张长12cm，宽10cm的矩形纸板，分别按照图1与图2两种方式裁去若干小正方形和小矩形，剩余部分（阴影部分）恰好做成无盖和有盖的长方体纸盒各一个.

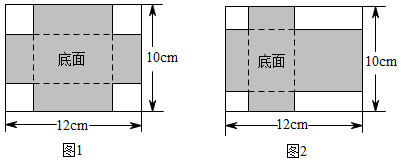(1)、做成有盖长方体纸盒的裁剪方式是（填“图1”或“图2”）.

(2)、已知图1中裁去的小正方形边长为1.5cm，求做成的纸盒的底面积.

(3)、已知按图2裁剪方式做成纸盒的底面积为24cm² ，则剪去的小正方形的边长为多少cm？

查看试题解析
24. 一学校为了绿化校园环境，向某园林公司购买力一批树苗，园林公司规定：如果购买树苗不超过60棵，每棵售价120元；如果购买树苗超过60棵，每增加1棵，所出售的这批树苗每棵售价均降低0.5元，但每棵树苗最低售价不得少于100元，该校最终向园林公司支付树苗款8800元，请问该校共购买了多少棵树苗？

查看试题解析
25. 如图， $▱ A B C D$ 中， $A B = 3 cm$ ， $B C = 5 cm$ ， $∠ B = 60 °$ ，点G是 $C D$ 的中点，点E是边 $A D$ 上的动点， $E G$ 的延长线与 $B C$ 的延长线交于点F，连接 $C E$ ， $D F$ .

(1)、求证：四边形 $C E D F$ 是平行四边形；

(2)、①直接写出：当 $A E =$ cm时，四边形 $C E D F$ 是菱形（不需要说明理由）；
②当 $A E =$ cm时，四边形 $C E D F$ 是矩形，请说明理由.

查看试题解析

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	59	96	116	290	480	601
摸到白球的频率 $\frac{m}{n}$		0.64	0.58		0.60	0.601