陕西省宝鸡市陇县2022年中考一模数学试卷

试卷更新日期：2022-05-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $（- 4 ）^{2}$ 的算术平方根是（）

A、﹣2 B、2 C、﹣4 D、4

查看试题解析
2. 下列图形不能由旋转得到的是（）

A、 B、 C、 D、

查看试题解析
3. 计算： ${(- \frac{1}{2} a b^{3})}^{2} =$ （）

A、 $- \frac{1}{2} a^{2} b^{6}$ B、 $\frac{1}{2} a^{2} b^{5}$ C、 $\frac{1}{4} a^{2} b^{6}$ D、 $- \frac{1}{4} a^{3} b^{5}$

查看试题解析
4. 如图，在 $△$ ABC中，AB＝AC，∠A＝40°，BD平分∠ABC的外角，CE平分∠ACB的外角，BD与CE的反向延长线相交于点F，则∠F＝（）

A、65° B、70° C、75° D、80°

查看试题解析
5. 如图，在菱形ABCD中， $∠ A = 120 °$ ，AB的长为4.点E，F，G，H分别为AB，BC，CD，DA边的中点，连接E，F，G，H，则在四边形EFGH中， $\frac{E F}{F G} =$ （）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
6. 如图，在平面直角坐标系中放置三个长为2，宽为1的长方形，已知一次函数y＝kx+b的图象经过点A与点B，则k与b的值为（）

A、k $= \frac{3}{2}$ ，b $= \frac{3}{4}$ B、k $= - \frac{3}{2}$ ，b $= - \frac{3}{4}$ C、k $= - \frac{3}{4}$ ，b $= - \frac{3}{2}$ D、k $= \frac{3}{4}$ ，b $= \frac{3}{2}$

查看试题解析
7. 如图，在 $△$ ABC中，AB＝AC，D在AC边上，E是BC边上一点，若AB＝3，AE＝2，∠AED＝∠B，则AD的长为（）

A、 $\frac{3}{5}$ B、 $\frac{3}{2}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
8. 已知点 $A (4 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (- 3 ， y_{3})$ 均在拋物线 $y = a x^{2} - 4 a x + c (a > 0)$ 上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析

二、填空题

9. 分解因式： $(- x^{3} + 6 x^{2} - 9 x) =$ .

查看试题解析
10. 若一个正多边形的每个内角度数都为108°，则这个正多边形的边数是.

查看试题解析
11. 七巧板又称七巧图、智慧板，是中国民间流传的智力玩具，它是由等腰直角三角形，正方形和平行四边形组成的.如图，若图形3中的一条直角边为 $\sqrt{2}$ ，那么整个七巧板所组成的正方形面积为.

查看试题解析
12. 如图，在平面直角坐标系中，O是坐标原点，在△OAB中，AO＝AB，AC⊥OB于点C，点A在反比例函数y $= \frac{k}{x}$ （k≠0）的图象上，若OB＝5，AC＝3，则k＝.

查看试题解析
13. 如图，正方形ABCD的边长为16，点E，F分别在线段AB，AD上，且AF＝8，AE＝6，若点P，Q分别在线段BC，CD上运动，G为线段PF上的点，在运动过程中，始终保持∠GEB＝∠GFA，则线段GQ的最小值为.

查看试题解析

三、解答题

14. 计算： $- 2 \times \sqrt[3]{- \frac{1}{8}} - | \sqrt{3} - 2 | + {(2022 - π)}^{0}$ .

查看试题解析
15. 解不等式组： ${\begin{matrix} 2 x + 3 > - 7 \\ \frac{- 2 x + 1}{2} \geq - 1 \end{matrix}$ ，并写出所有整数解.

查看试题解析
16. 化简：（ $\frac{- a - 2}{a - 1} -$ a﹣2）÷（a+2）.

查看试题解析
17. 如图，已知 $△ A B C$ ，请用尺规作图法，在AC边上求作一点D，使得 $B D = D C$ .（保留作图痕迹，不写作法）

查看试题解析
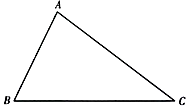18. 如图，在 $△$ ABC中，已知CD⊥AB于点D，BE⊥AC于点E，∠DCB＝∠EBC.求证：AD＝AE.

查看试题解析
19. 3月12日植树节，学校组织学生去植树、栽花.某校九年级（1）班领到一批树苗和花苗共380棵.已知一名学生一天能完成4棵树或10株花的栽种任务.若九年级（1）班的50名学生要按时完成此次任务，班长该如何分配植树和栽花的人数.

查看试题解析
20. 第24届北京冬奥会的开幕式中，“二十四节气的开幕式倒计时”向全世界人民展示了中华文化源远流长的特点，尽显中国式浪漫.杨老师为了让学生深入的了解二十四节气，将每个节气的名称写在形状大小都一样的小卡片上，并将卡片倒扣在桌面上，邀请同学上讲台随机抽取一张卡片，并向大家介绍卡片上对应节气的含义.

(1)、请问随机抽取一张卡片，上面写有“立春”的概率为；

(2)、若老师将属于春季的“立春、雨水，惊蛰、春分、清明、谷雨”六张卡片单独拿出，邀请小明和小华同时抽取.请利用画树状图或列表的方法，求两人抽到的卡片上写有相同的字的概率.

查看试题解析
21. 某小区有一露天舞台，横截面如图所示.AC垂直于地面，AB表示楼梯，AE为舞台面，楼梯的坡度为1，坡长 $A B = 3 m$ .为保障安全，小区决定对该楼梯进行改造，降低坡度，拟修新楼梯AD，使新坡度调整为 $\frac{1}{2}$ .

(1)、求舞台的高AC（结果保留根号）；

(2)、求AD的长度（结果保留根号）.

查看试题解析
22. 小强在学习完统计知识后，对自己班上的同学上学方式进行调查统计，他通过收集数据后绘制的两幅不完整的统计图如图所示.请你根据图中提供的信息解答下列问题：

(1)、补全条形统计图，此次抽样调查的众数为 .

(2)、在扇形统计图中，表示“骑车”部分的扇形所对应的圆心角是多少度？

(3)、若全年级共有1000名学生，估计全年级步行上学的学生有多少名？

查看试题解析
23. 甲、乙两人分别从同一公路上的A，B两地同时出发骑车前往C地，两人离A地的距离y（km）与甲行驶的时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：

(1)、A，B两地相距km；乙骑车的速度是km/h；

(2)、求甲追上乙时用了多长时间.

查看试题解析
24. 如图，AD是⊙O的直径， $\overset{⌢}{A B} = \overset{⌢}{B C}$ ，BD交AC于点E，点F在DB的延长线上，且∠BAF＝∠C.

(1)、求证：AF是⊙O的切线；

(2)、若BD＝8，BE＝6，求AB的长.

查看试题解析
25. 已知二次函数y＝mx²+4x+2的图象经过点A(3，﹣4).

(1)、求m的值；

(2)、已知函数与y轴交于点C，连接AC.请问在函数y＝mx²+4x+2的图象上，是否存在一点M，使得 $△$ ACM为等腰三角形，且AC边为底，若存在，求出满足条件的M点坐标；若不存在，请说明理由.

查看试题解析
26. 在学习完“图形的旋转”后，某数学兴趣小组做了如下探究 $△$ ABC和 $△$ DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°， $△$ DEF的顶点E与 $△$ ABC的斜边BC的中点重合.将 $△$ DEF绕点E作逆时针旋转，该过程中，线段DE与线段AB相交于点P，线段EF与射线CM相交于点Q.

(1)、问题提出：如图①，当点Q在线段AC上，且AP＝AQ时， $△$ BPE和 $△$ CQE是否全等.如果全等，写出证明过程；若不赞同，请说明理由.

(2)、问题解决：如图②，当点Q在线段CA的延长线上时， $△$ BPE和 $△$ CQE是否有存在与第（1）问相同的关系，如果相同写出证明过程；如果不同，请说明它们的关系.当BP＝a，CQ $= \frac{9}{2}$ a时，求P，Q两点间的距离（用含a的代数式表示）.

查看试题解析