陕西省宝鸡市凤翔区2022届九年级下学期第一次质量检测追踪训练卷数学试卷（一模）
试卷更新日期：2022-05-24 类型：中考模拟
一、单选题
-
1. 规定：（→1）表示向右移动1记作＋1，则（←2）表示向左移动2记作（ ）A、＋2 B、－2 C、－12 D、＋122. 4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439000米.将439000用科学记数法表示应为（ ）A、 4.39×105 B、4.39×106 C、0.439×106 D、439×1033. 如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②.关于平移前后几何体的三视图，下列说法正确的是（ ）
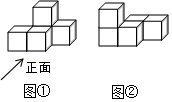A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同4. 下列运算正确的是（ ）A、a2＋3a2＝4a4 B、（－3a2b）2＝6a4b2 C、（a－1）2＝a2－1 D、2a2b÷b＝2a25. 一副直角三角板如图放置，点C在FD的延长线上，AB//CF，∠F=∠ACB=90°，则∠DBC的度数为（ ）
A、10° B、15° C、18° D、30°6. 已知A（x1 ， y1），B（x2 ， y2）是一次函数y＝（a－2）x＋1图象上不同的两个点，若（x1－x2）（y1－y2）＜0，则a的取值范围是（ ）A、a＜0 B、a＞0 C、a＜2 D、a＞27. 如图，C，D是以线段AB为直径的⊙O上两点（位于AB两侧），CD＝AD，且∠ABC＝70°，则∠BAD的度数是（ ）
A、50° B、45° C、35° D、30°8. 已知抛物线y＝ax2＋bx＋c过点（－1，0）和点（0，－3），且顶点在第四象限，设M＝4a＋2b＋c，则M的取值范围是（ ）A、－9＜M＜0 B、－18＜M＜0 C、0＜M＜9 D、－9＜M＜9二、解答题
-
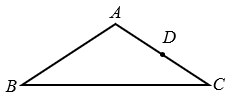
9. 计算：（－ ）－1＋|2－ |－2×（－ ）210. 解不等式： －x ＜－ ，并在数轴上表示解集.11. 化简： .12. 如图，在等腰△ABC中，AB＝AC，点D是AC边上一定点.请用尺规作图法在BC上求作一点P，使得△ABC∽△PCD.（保留作图痕迹，不写作法）
13. 如图，在矩形 ABCD中，点 E，F 在对角线BD．请添加一个条件，使得结论“AE=CF”成立，并加以证明．
14. 为了进一步丰富校园活动，学校准备购买一批足球和篮球，购买2个篮球和3个足球共需425元，购买3个篮球和4个足球所花的钱一样多.(1)、求篮球和足球的单价各是多少？(2)、若学校购买15个篮球8个足球共需多少元？15. 第十四届全运会以陕西的“秦岭四宝”朱鹮、大熊猫、羚牛和金丝猴为原型，设计了“朱朱”、“熊熊”、“羚羚”和“金金”四个运动吉祥物.小颖国庆假期来西安游玩，想从这四个全运会吉祥物中任意选购两个不同的玩偶，带回家后送给弟弟和妹妹.
(1)、小颖第一个玩偶选购“羚羚”的概率为；(2)、请利用列表或画树状图的方法，求小颖选购“朱朱”和“羚羚”的概率.16. 如图，在某小区内拐角处的一段道路上，有一儿童在C处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的A处驶来. 已知MO=4m，CO=5m，DO=3m，∠AOD=70°，汽车从A处前行多少米，才能发现C处的儿童（结果保留整数）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75；sin70°≈0.94，cos70°≈0.34，tan70°≈2.75.）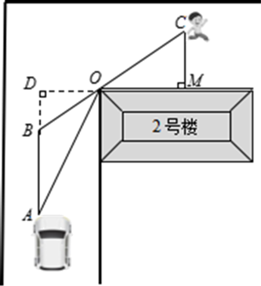
17. 为了解“双减”政策落地效果，及时反映家长的诉求与期盼，共同促进学生的全面发展和健康成长，某校随机抽取部分学生家长（每生只选一位家长）开展了关于“双减”政策影响情况的专题调研.其中，对于“课后服务工作的满意度”的调查分为“A—很满意”、“B—比较满意”、“C—不太满意”、“D—不满意”四个选项，请家长予以评分，并根据调查结果绘制了以下两幅统计图：“课后服务工作的满意度”调查统计图.
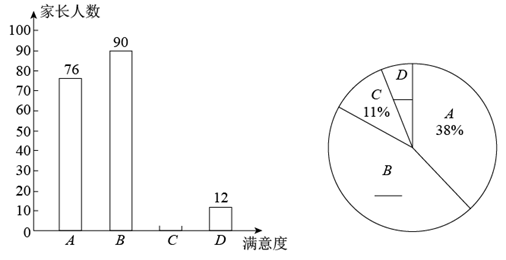
请你根据统计图中的信息，解答下列问题：
(1)、补全两幅统计图；(2)、请求出本次“课后服务工作的满意度”调查的平均分；(3)、已知该校共有2600名学生，请估计有多少名学生家长对“课后服务工作的满意度”持“很满意”或“比较满意”的态度？18. 由于连降暴雨，某水库水位不断上涨.暴雨停止后，经勘测发现，水库水位已经超过警戒线水位.防汛指挥部指令，将五个水流量相同的泄洪闸打开紧急泄洪.6小时后水位降到了警戒线以下，关闭三个泄洪闸减少水流量继续泄洪.水库水位y（m）与泄洪时间x（h）的关系如图所示，根据图象解答下列问题.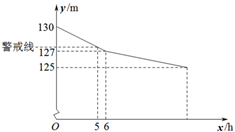
(1)、当0≤x≤6时，求y 与 x之间的函数关系式；(2)、该水库的警戒线水位为多少？(3)、若水位高度降至125米时关闭所有泄洪闸，此次泄洪共持续多长时间？19. 如图，在Rt△ABC中，∠BAC＝90°，以AB为直径的⊙O交斜边BC于点E，过点E作⊙O的切线交AC边于点D.求证：
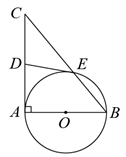(1)、CD＝DE；(2)、若BE＝2，BC＝8，求AC的长.20. 如图，抛物线C1：y＝ax2＋2x＋c与x轴交于点A、B两点，且经过直线y=－x－3与两轴的交点A、C，其顶点为D.
(1)、求抛物线C1的表达式及D点坐标；(2)、将抛物线C1向右平移，使得平移后的抛物线C2与抛物线C1交于点P，且∠PAB＝∠DAC，求平移后的抛物线C2的表达式.21.
(1)、问题提出
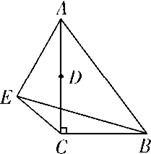
如图1，点A为线段BC外一动点，且BC=5，AB=2，填空：当点A位于时，线段AC的长取得最大值，且最大值是；(2)、问题探究如图2，在Rt△ABC中，AB=AC，点D为△ABC外一点，且BD=10，CD=4，求AD的最小值；
(3)、问题解决如图3，市政部门计划在一片足够大的空地上修建四边形的城市花园ABCD，其中AB=200米，BC=CD，BC⊥CD，BC∥AD，由于受地理位置影响，∠BAD＜90°.根据要求，现计划给该城市花园修建一条笔直的景观路，且景观路的入口定为AB的中点O，出口定为点C，为了尽可能地提高观赏体验，要求景观路OC尽可能的长，试求景观路OC最长为多少米？
三、填空题
-
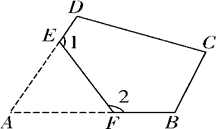
22. 如图，将四边形ABCD裁掉一个40°的角得到一个五边形BCDEF，则∠1＋∠2＝.
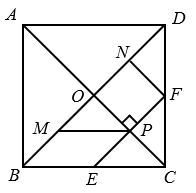
23. 七巧板是一种古老的中国传统智力玩具.如图，在正方形纸板ABCD中，BD为对角线，E、F分别为BC、CD的中点，AP⊥EF分别交BD、EF于O、P两点，M、N分别为BO、DO的中点，连接MP、NF，沿图中实线剪开即可得到一副七巧板.若AB＝1，则四边形BMPE的面积是.
