备考浙教版中考数学题型专项训练 二次函数解答题专练
试卷更新日期:2022-05-23 类型:三轮冲刺
一、综合题
-
1. 如图1,在⊙O中,M为弦AB的中点,过点M作直径CD,E为线段OM上一点,连结AE并延长交⊙O于点F,连结BF,AE=BF.
 (1)、证明:AC=BF.(2)、当时,求.(3)、如图2,连结CF交AB于点G,当CD=2时,设EM=x, , 求y关于x的函数解析式,并确定y的最大值.2. 在平面直角坐标系中,点O为坐标系的原点.抛物线分别交x轴于点、点 , 交y轴于点C.
(1)、证明:AC=BF.(2)、当时,求.(3)、如图2,连结CF交AB于点G,当CD=2时,设EM=x, , 求y关于x的函数解析式,并确定y的最大值.2. 在平面直角坐标系中,点O为坐标系的原点.抛物线分别交x轴于点、点 , 交y轴于点C.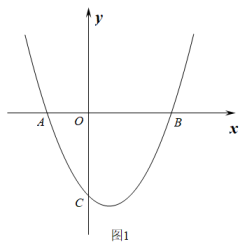

 (1)、如图1,求抛物线的解析式;(2)、如图2,点P为抛物线第二象限上的点,连接BP交y轴于点D,设点P的横坐标为t,CD的长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,点F、N分别在BD、OA上,连接NF,且 , 点E在OC上,连接NE、FE, , 点K在FN上,且 . 当 , 时,求点P坐标.3. 如图,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,连接BC.
(1)、如图1,求抛物线的解析式;(2)、如图2,点P为抛物线第二象限上的点,连接BP交y轴于点D,设点P的横坐标为t,CD的长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,点F、N分别在BD、OA上,连接NF,且 , 点E在OC上,连接NE、FE, , 点K在FN上,且 . 当 , 时,求点P坐标.3. 如图,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,连接BC.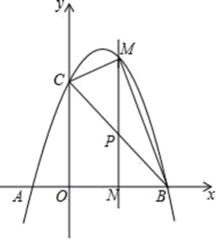 (1)、求抛物线的解析式;(2)、若点P为线段BC上的一动点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)、在(2)的条件下,当△BCM的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A、P、D、E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.4. 抛物线与x轴交于A,B两点,与y轴交于点C,已知点 , 抛物线的最低点的坐标为 .
(1)、求抛物线的解析式;(2)、若点P为线段BC上的一动点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)、在(2)的条件下,当△BCM的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A、P、D、E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.4. 抛物线与x轴交于A,B两点,与y轴交于点C,已知点 , 抛物线的最低点的坐标为 . (1)、求出该抛物线的函数解析式;(2)、如图1,线段BC绕点C逆时针旋转90°得到线段CD线段,CD与抛物线相交于点E,求点E的坐标.(3)、如图2,点M,N是线段AC上的动点,且 , 求△OMN周长的最小值.5. 如图所示,在平面直角坐标系中,抛物线L:y=x2bx+c与直线l1:y=﹣x+1交于点A,且点A的横坐标为﹣4,设抛物线的顶点为M,点N(0,n)是y轴上一点,过点N作直线l2x轴.
(1)、求出该抛物线的函数解析式;(2)、如图1,线段BC绕点C逆时针旋转90°得到线段CD线段,CD与抛物线相交于点E,求点E的坐标.(3)、如图2,点M,N是线段AC上的动点,且 , 求△OMN周长的最小值.5. 如图所示,在平面直角坐标系中,抛物线L:y=x2bx+c与直线l1:y=﹣x+1交于点A,且点A的横坐标为﹣4,设抛物线的顶点为M,点N(0,n)是y轴上一点,过点N作直线l2x轴. (1)、请用含b的代数式表示c;(2)、若直线l2在点M的上方,且点M到直线l2的距离为2,求n的最大值;(3)、若点B在直线l1上,且点B的横坐标为﹣2,点C( , 3),若抛物线L与线段BC有公共点,结合图像,直接写出b的取值范围.6. 如图,已知抛物线经过两点 , , 是抛物线与轴的交点.
(1)、请用含b的代数式表示c;(2)、若直线l2在点M的上方,且点M到直线l2的距离为2,求n的最大值;(3)、若点B在直线l1上,且点B的横坐标为﹣2,点C( , 3),若抛物线L与线段BC有公共点,结合图像,直接写出b的取值范围.6. 如图,已知抛物线经过两点 , , 是抛物线与轴的交点. (1)、求抛物线的解析式和点坐标;(2)、点在平面直角坐标系第一象限内的抛物线上运动,设的面积为 , 求关于的函数表达式(指出自变量的取值范围)和的最大值.7. 如图,抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,顶点为D,点B的坐标为(3,0).
(1)、求抛物线的解析式和点坐标;(2)、点在平面直角坐标系第一象限内的抛物线上运动,设的面积为 , 求关于的函数表达式(指出自变量的取值范围)和的最大值.7. 如图,抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,顶点为D,点B的坐标为(3,0). (1)、填空:点A的坐标为 , 点D的坐标为 , 抛物线的解析式为 .(2)、当二次函数y=x2+bx+c的自变量x满足m≤x≤m+2时,函数y的最小值为 , 求m的值;8. 定义:点P(m,m)是平面直角坐标系内一点,将函数l的图象位于直线x=m左侧部分,以直线y=m为对称轴翻折,得到新的函数l′的图象,我们称函数l′的函数是函数l的相关函数,函数l′的图象记作F1 , 函数l的图象未翻折的部分记作F2 , 图象F1和F2合起来记作图象F.
(1)、填空:点A的坐标为 , 点D的坐标为 , 抛物线的解析式为 .(2)、当二次函数y=x2+bx+c的自变量x满足m≤x≤m+2时,函数y的最小值为 , 求m的值;8. 定义:点P(m,m)是平面直角坐标系内一点,将函数l的图象位于直线x=m左侧部分,以直线y=m为对称轴翻折,得到新的函数l′的图象,我们称函数l′的函数是函数l的相关函数,函数l′的图象记作F1 , 函数l的图象未翻折的部分记作F2 , 图象F1和F2合起来记作图象F.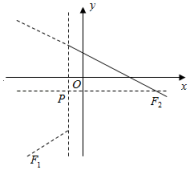
例如:函数l的解析式为y=x2﹣1,当m=1时,它的相关函数l′的解析式为y=﹣x2+3(x<1).
(1)、如图,函数l的解析式为y=﹣x+2,当m=﹣1时,它的相关函数l′的解析式为y= .(2)、函数l的解析式为y=﹣ , 当m=0时,图象F上某点的纵坐标为﹣2,求该点的横坐标.(3)、已知函数l的解析式为y=x2﹣4x+3,①已知点A、B的坐标分别为(0,2)、(6,2),图象F与线段AB只有一个公共点时,结合函数图象,求m的取值范围;
②若点C(x,n)是图象F上任意一点,当m﹣2≤x≤5时,n的最小值始终保持不变,求m的取值范围(直接写出结果).
9. 如图,在平面直角坐标系中,抛物线ybx+c与x轴交于A(﹣2,0)、B(4,0)两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点,连接OP交BC于点Q.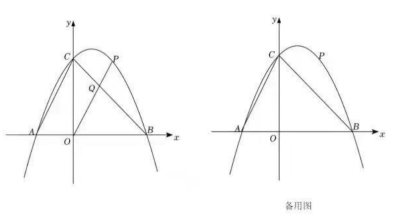 (1)、求抛物线的函数表达式;(2)、当的值最大时,求点P的坐标和的最大值;(3)、把抛物线ybx+c沿射线AC方向平移个单位得新抛物线y',M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,直接写出N点的坐标.10. 如图,在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)、求抛物线的函数表达式;(2)、当的值最大时,求点P的坐标和的最大值;(3)、把抛物线ybx+c沿射线AC方向平移个单位得新抛物线y',M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,直接写出N点的坐标.10. 如图,在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.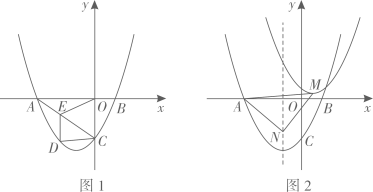 (1)、求点A的坐标;(2)、如图1,连接AC,点D为线段AC下方抛物线上一动点,过点D作DE∥y轴交线段AC于E点,连接EO,记△ADC的面积为 ,△AEO的面积为 ,求 的最大值及此时点D的坐标;(3)、如图2,将抛物线沿射线CB方向平移 个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线的顶点,当△AMN为以AM为腰的等腰三角形时,请直接写出点N的坐标.11. 如图1,抛物线经过点A(4,3),对称轴是直线=2,顶点为B.抛物线与轴交于点C,连接AC,过点A作AD⊥轴于点D,点E是线段AC上的动点(点E不与A、C两点重合).
(1)、求点A的坐标;(2)、如图1,连接AC,点D为线段AC下方抛物线上一动点,过点D作DE∥y轴交线段AC于E点,连接EO,记△ADC的面积为 ,△AEO的面积为 ,求 的最大值及此时点D的坐标;(3)、如图2,将抛物线沿射线CB方向平移 个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线的顶点,当△AMN为以AM为腰的等腰三角形时,请直接写出点N的坐标.11. 如图1,抛物线经过点A(4,3),对称轴是直线=2,顶点为B.抛物线与轴交于点C,连接AC,过点A作AD⊥轴于点D,点E是线段AC上的动点(点E不与A、C两点重合). (1)、求抛物线的函数解析式和顶点B的坐标;(2)、若直线BE将四边形ACOD分成面积比为1:3的两个四边形,求点E的坐标;(3)、如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在轴上的同时点F也恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.12. 已知二次函数 与 轴交于 , 两点(其中 在 的左侧),且 .
(1)、求抛物线的函数解析式和顶点B的坐标;(2)、若直线BE将四边形ACOD分成面积比为1:3的两个四边形,求点E的坐标;(3)、如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在轴上的同时点F也恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.12. 已知二次函数 与 轴交于 , 两点(其中 在 的左侧),且 .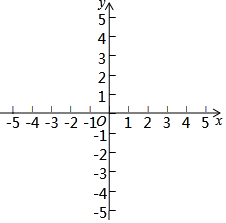 (1)、抛物线的对称轴是.(2)、求点 和点 坐标.(3)、点 坐标为 , .若抛物线 与线段 恰有一个交点,求 的取值13. 如图,已知 中, , , 点坐标为 , 点坐标为 ,抛物线 的顶点记为 ,且经过 的三个顶点 、 、 (点 在点 左侧,点 在 轴下方).抛物线 也交 轴于点 、 ,其顶点为 .
(1)、抛物线的对称轴是.(2)、求点 和点 坐标.(3)、点 坐标为 , .若抛物线 与线段 恰有一个交点,求 的取值13. 如图,已知 中, , , 点坐标为 , 点坐标为 ,抛物线 的顶点记为 ,且经过 的三个顶点 、 、 (点 在点 左侧,点 在 轴下方).抛物线 也交 轴于点 、 ,其顶点为 .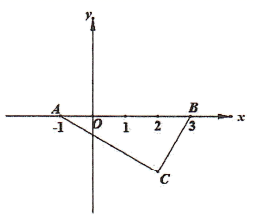 (1)、求 点的坐标和抛物线 的顶点 的坐标.(2)、当 的值最小时,求抛物线 的解析式.(3)、设点 是抛物线 上的一个动点,且位于其对称轴的右侧.若 是与 相似的三角形,求抛物线 的顶点 的坐标.14. 如图,抛物线的图象经过点C(0,2),交x轴于点A(﹣1,0)和B,连接BC,直线y=kx+1与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)、求 点的坐标和抛物线 的顶点 的坐标.(2)、当 的值最小时,求抛物线 的解析式.(3)、设点 是抛物线 上的一个动点,且位于其对称轴的右侧.若 是与 相似的三角形,求抛物线 的顶点 的坐标.14. 如图,抛物线的图象经过点C(0,2),交x轴于点A(﹣1,0)和B,连接BC,直线y=kx+1与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.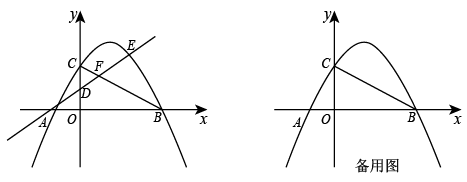 (1)、求抛物线的表达式及点B的坐标;(2)、求的最大值及此时点E的坐标;(3)、在(2)的条件下,若点M为直线DE上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B、D、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.15. 如图,在平面直角坐标系中,二次函数yx2+bx﹣2的图象与x轴交于点A和点B(4,0),与y轴交于点C.
(1)、求抛物线的表达式及点B的坐标;(2)、求的最大值及此时点E的坐标;(3)、在(2)的条件下,若点M为直线DE上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B、D、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.15. 如图,在平面直角坐标系中,二次函数yx2+bx﹣2的图象与x轴交于点A和点B(4,0),与y轴交于点C. (1)、求二次函数的表达式;(2)、若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;(3)、若点Q在第四象限内,且tan∠AQB , M(﹣2,1),线段MQ是否存在最大值,如果存在,求出最大值;如果不存在,请说明理由.16. 在平面直角坐标系中,O为坐标原点,抛物线交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴于点C,连接AC,且 .
(1)、求二次函数的表达式;(2)、若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;(3)、若点Q在第四象限内,且tan∠AQB , M(﹣2,1),线段MQ是否存在最大值,如果存在,求出最大值;如果不存在,请说明理由.16. 在平面直角坐标系中,O为坐标原点,抛物线交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴于点C,连接AC,且 .

 (1)、如图1,求抛物线的解析式;(2)、如图2,点P在第三象限的抛物线上,连接BP交y轴于点D,设点P横坐标为t,线段CD的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、如图2,在(2)的条件下,点E在线段OB上,且 , 连接DE,F在y轴正半轴上,连接BF交抛物线于点G, , 若 , 求点G的坐标.17. 如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连接OB.点P为抛物线上AB上方的一个点,连接PA,作PQ⊥AB垂足为H,交OB于点Q.
(1)、如图1,求抛物线的解析式;(2)、如图2,点P在第三象限的抛物线上,连接BP交y轴于点D,设点P横坐标为t,线段CD的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、如图2,在(2)的条件下,点E在线段OB上,且 , 连接DE,F在y轴正半轴上,连接BF交抛物线于点G, , 若 , 求点G的坐标.17. 如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连接OB.点P为抛物线上AB上方的一个点,连接PA,作PQ⊥AB垂足为H,交OB于点Q. (1)、求AB的长;
(1)、求AB的长;
(2)、当∠APQ=∠B时,求点P的坐标;
(3)、当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.
18. 小明购进一些糖果,把这些糖果进行包装后销售,包装后每千克售价为30元,已知购进糖果的总价(元)与数量x(千克)之间满足如图所示的二次函数 , 这些糖果的包装总费用(元)与数量x(千克)满足一次函数 . (1)、求与x之间的函数关系式;(2)、若小明购进的糖果不少于8千克且不多于10千克,他最多能获得多少利润?最少能获得多少利润?19. 某水产养殖户利用温棚养殖技术养殖南美白虾,与传统养殖相比,可缩短养殖周期,即从原来的每年养殖两季提高至每年三季,已知每千克白虾的养殖成本为8元,在某上市周期的70天里,销售单价p(元/千克)与时间第t(天)之间的函数关系如下:
(1)、求与x之间的函数关系式;(2)、若小明购进的糖果不少于8千克且不多于10千克,他最多能获得多少利润?最少能获得多少利润?19. 某水产养殖户利用温棚养殖技术养殖南美白虾,与传统养殖相比,可缩短养殖周期,即从原来的每年养殖两季提高至每年三季,已知每千克白虾的养殖成本为8元,在某上市周期的70天里,销售单价p(元/千克)与时间第t(天)之间的函数关系如下:日销售量y(千克)与时间第t(天)之间的函数关系如右图所示:
 (1)、求日销售量y与时间t的函数关系式;(2)、求第几天的日销售利润最大?最大利润是多少元?(3)、在实际销售的前40天(1≤t≤40,t为整数)中,该养殖户决定每销售1千克白虾,就捐赠m(m<8)元给公益事业.在这前40天中,已知每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.20. 某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价﹣制造成本)(1)、写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;(2)、当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?(3)、根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?21. 如图,已知抛物线y=x2+bx+c与x轴交于点A、B,AB=2,与y轴交于点C,对称轴为直线x=2,对称轴交x轴于点M.
(1)、求日销售量y与时间t的函数关系式;(2)、求第几天的日销售利润最大?最大利润是多少元?(3)、在实际销售的前40天(1≤t≤40,t为整数)中,该养殖户决定每销售1千克白虾,就捐赠m(m<8)元给公益事业.在这前40天中,已知每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.20. 某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价﹣制造成本)(1)、写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;(2)、当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?(3)、根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?21. 如图,已知抛物线y=x2+bx+c与x轴交于点A、B,AB=2,与y轴交于点C,对称轴为直线x=2,对称轴交x轴于点M.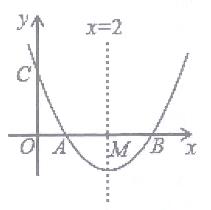 (1)、求抛物线的函数解析式;(2)、设P为对称轴上一动点,求△APC周长的最小值;(3)、设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是菱形,则点D的坐标为 .22.
(1)、求抛物线的函数解析式;(2)、设P为对称轴上一动点,求△APC周长的最小值;(3)、设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是菱形,则点D的坐标为 .22.如图,抛物线l1:y=x2﹣4的图象与x轴交于A,C两点,抛物线l2与l1关于x轴对称.
 (1)、直接写出l2所对应的函数表达式;(2)、若点B是抛物线l2上的动点(B与A,C不重合),以AC为对角线,A,B,C三点为顶点的平行四边形的第四个顶点为D,求证:D点在l2上.(3)、当点B位于l1在x轴下方的图象上,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它面积的最值;若不存在,请说明理由.23. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
(1)、直接写出l2所对应的函数表达式;(2)、若点B是抛物线l2上的动点(B与A,C不重合),以AC为对角线,A,B,C三点为顶点的平行四边形的第四个顶点为D,求证:D点在l2上.(3)、当点B位于l1在x轴下方的图象上,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它面积的最值;若不存在,请说明理由.23. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
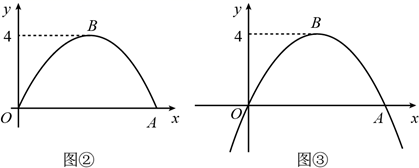 (1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.24. 为促进经济发展,方便居民出行.某施工队要修建一个横断面为抛物线的公路隧道.抛物线的最高点P离路面OM的距离为6m,宽度OM为12m.
(1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.24. 为促进经济发展,方便居民出行.某施工队要修建一个横断面为抛物线的公路隧道.抛物线的最高点P离路面OM的距离为6m,宽度OM为12m.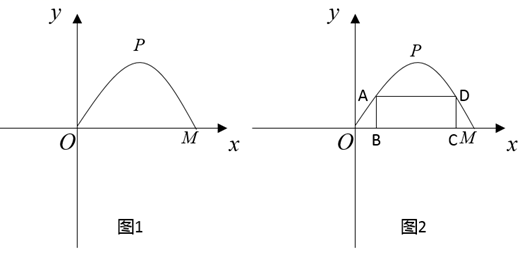 (1)、按如图所示的平面直角坐标系,求表示该抛物线的函数表达式;(2)、一货运汽车装载某大型设备后高为4m,宽为3.5m.如果该隧道内设双向行车道(正中间是一条宽1m的隔离带),那么这辆货车能否安全通过?(3)、施工队计划在隧道口搭建一个矩形“脚手架”ABCD,使A,D点在抛物线上.B,C点在地面OM线上(如图2所示).为了筹备材料,需求出“脚手架”三根支杆AB,AD,DC的长度之和的最大值是多少?请你帮施工队计算一下.25. 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:
(1)、按如图所示的平面直角坐标系,求表示该抛物线的函数表达式;(2)、一货运汽车装载某大型设备后高为4m,宽为3.5m.如果该隧道内设双向行车道(正中间是一条宽1m的隔离带),那么这辆货车能否安全通过?(3)、施工队计划在隧道口搭建一个矩形“脚手架”ABCD,使A,D点在抛物线上.B,C点在地面OM线上(如图2所示).为了筹备材料,需求出“脚手架”三根支杆AB,AD,DC的长度之和的最大值是多少?请你帮施工队计算一下.25. 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型;②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
 (1)、如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)、如果设计成圆弧型,求该圆弧所在圆的半径;(3)、在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.26. 如图①,小明和小亮分别站在平地上的 两地先后竖直向上抛小球 (抛出前两小球在同一水平面上),小球到达最高点后会自由竖直下落到地面. 两球到地面的距离 和 与小球A离开小明手掌后运动的时间 之间的函数图象分别是图②中的抛物线 .已知抛物线 经过点 ,顶点是 ,抛物线 经过 和 两点,两抛物线的开口大小相同.
(1)、如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)、如果设计成圆弧型,求该圆弧所在圆的半径;(3)、在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.26. 如图①,小明和小亮分别站在平地上的 两地先后竖直向上抛小球 (抛出前两小球在同一水平面上),小球到达最高点后会自由竖直下落到地面. 两球到地面的距离 和 与小球A离开小明手掌后运动的时间 之间的函数图象分别是图②中的抛物线 .已知抛物线 经过点 ,顶点是 ,抛物线 经过 和 两点,两抛物线的开口大小相同. (1)、分别求出 与x之间的函数表达式.(2)、在小球B离开小亮手掌到小球A落到地面的过程中.
(1)、分别求出 与x之间的函数表达式.(2)、在小球B离开小亮手掌到小球A落到地面的过程中.①当x的值为 ▲ 时,两小球到地面的距离相等;
②当x为何值时,两小球到地面的距离之差最大?最大是多少?
27. 女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某女生在O处将球垫偏,之后又在A, B两处先后垫球,球沿抛物线C1 → C2 → C3运动(假设抛物线C1 , C2 , C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点A( , ),点B的横坐标为 - ,抛物线C1和C3的表达式分别为 y = ax2- 2ax 和 y = 2ax2 + bx (a≠ 0).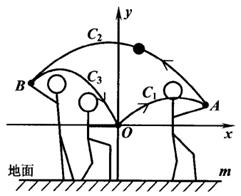 (1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?28. 一台自动喷灌设备的喷流情况如图所示,设水管在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成 角,水流最高点B比喷头A高2米.
(1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?28. 一台自动喷灌设备的喷流情况如图所示,设水管在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成 角,水流最高点B比喷头A高2米.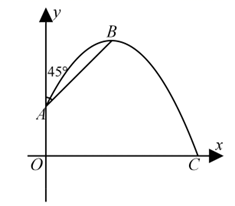 (1)、求抛物线解析式;(2)、求水流落地点C到O的距离;(3)、若水流的水平位移s米(抛物线上两对称点之间的距离)与水流的运动时间t之间的函数关系为 ,求共有几秒钟,水流的高度不低于2米?29. 如图所示,某公园在一块扇形0EF草坪上的圆心0处垂直于草坪的地上竖一根柱子OA,在A处安装一个自动喷水装置.喷头向外喷水.连喷头在内,柱高 米,水流在各个方向上沿形状相同的抛物线路径落下.喷出的水流在与0点的水平距离4米处达到最高点B,点B距离地面2米.当喷头A旋转120°时,这块草坪可以全被水覆盖·
(1)、求抛物线解析式;(2)、求水流落地点C到O的距离;(3)、若水流的水平位移s米(抛物线上两对称点之间的距离)与水流的运动时间t之间的函数关系为 ,求共有几秒钟,水流的高度不低于2米?29. 如图所示,某公园在一块扇形0EF草坪上的圆心0处垂直于草坪的地上竖一根柱子OA,在A处安装一个自动喷水装置.喷头向外喷水.连喷头在内,柱高 米,水流在各个方向上沿形状相同的抛物线路径落下.喷出的水流在与0点的水平距离4米处达到最高点B,点B距离地面2米.当喷头A旋转120°时,这块草坪可以全被水覆盖·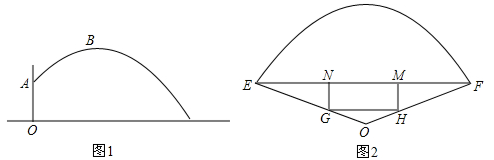 (1)、建立适当的平面直角坐标系,使A的坐标为(0, ),水流的最高点B的坐标为(4,2),求出此平面直角坐标系中抛物线水流对应的函数解析式;(2)、求喷水装置能喷灌的草坪的面积(结果用含 的式子表示)(3)、在扇形OEF的一块三角形区域地块△OEF中,现要建造一个矩形GHMN花坛,如图②的设计方案是使H,G分别在OF,OE上,MN在EF上,设MN=2X米,当X取何值时,矩形GHMN花坛的面积最大?30. 如图,在平面直角坐标系xOy中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,其中A(﹣1,0),C(0,3).
(1)、建立适当的平面直角坐标系,使A的坐标为(0, ),水流的最高点B的坐标为(4,2),求出此平面直角坐标系中抛物线水流对应的函数解析式;(2)、求喷水装置能喷灌的草坪的面积(结果用含 的式子表示)(3)、在扇形OEF的一块三角形区域地块△OEF中,现要建造一个矩形GHMN花坛,如图②的设计方案是使H,G分别在OF,OE上,MN在EF上,设MN=2X米,当X取何值时,矩形GHMN花坛的面积最大?30. 如图,在平面直角坐标系xOy中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,其中A(﹣1,0),C(0,3). (1)、求该抛物线的解析式;(2)、如图1,点D,E是线段BC上的两点(E在D的右侧), , 过点D作DP∥y轴,交直线BC上方抛物线于点P,过点E作EF⊥x轴于点F,连接FD,FP,当△DFP面积最大时,求点P的坐标及△DFP面积的最大值;(3)、如图2,在(2)取得面积最大的条件下,连接BP,将线段BP沿射线BC方向平移,平移后的线段记为B'P',G为y轴上的动点,是否存在以B'P'为直角边的等腰Rt△GB'P'?若存在,请直接写出点G的坐标,若不存在,请说明理由.31. 如图1,在Rt△ABC中∠ACB=90°,∠BAC=30°,AB=4cm.点P是以AC为直径的半圆上的动点,设C,P两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.根据学习函数的经验,小宇分别对函数y1 , y2随自变量x的变化而变化的规律进行了探究.下面是小宇的探究过程,请补充完整:
(1)、求该抛物线的解析式;(2)、如图1,点D,E是线段BC上的两点(E在D的右侧), , 过点D作DP∥y轴,交直线BC上方抛物线于点P,过点E作EF⊥x轴于点F,连接FD,FP,当△DFP面积最大时,求点P的坐标及△DFP面积的最大值;(3)、如图2,在(2)取得面积最大的条件下,连接BP,将线段BP沿射线BC方向平移,平移后的线段记为B'P',G为y轴上的动点,是否存在以B'P'为直角边的等腰Rt△GB'P'?若存在,请直接写出点G的坐标,若不存在,请说明理由.31. 如图1,在Rt△ABC中∠ACB=90°,∠BAC=30°,AB=4cm.点P是以AC为直径的半圆上的动点,设C,P两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.根据学习函数的经验,小宇分别对函数y1 , y2随自变量x的变化而变化的规律进行了探究.下面是小宇的探究过程,请补充完整:
⑴
⑵
⑶
(1)、根据点P在半圆上的不同位置,画出相应的图形,测量线段CP,BP,AP的长度,得到下表的几组对应值:x/cm
0
1
2
3
3.5
y1/cm
2
3
3.8
4.4
4
y2/cm
3.5
3.3
2.8
1.7
0
(2)、①如图2,在平面直角坐标系xOy中,画出了函数y1的图象,请在同一坐标系中,描点并画出函数y2的图象;②结合函数图象填空:当x≈ ▲ cm时,y1=y2;当y1<y2时,x的取值范围是 ▲ ;(结果精确到0.1cm)(3)、当PA=PC时,结合函数图象写出线段CP与BP的长.(结果精确到0.1cm)32. 已知二次函数y=x2+2bx+c(1)、若b=c,是否存在实数x,使得相应的y的值为1?请说明理由;(2)、若b=c﹣2,y在﹣2≤x≤2上的最小值是﹣3,求b的值.