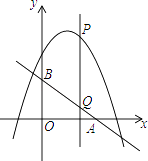备考浙教版中考数学题型专项训练 二次函数填空题专练
试卷更新日期:2022-05-23 类型:二轮复习
一、填空题
-
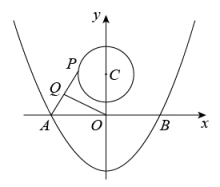
1. 如图,抛物线与x轴交于A、B两点,P是以点为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最小值是 .
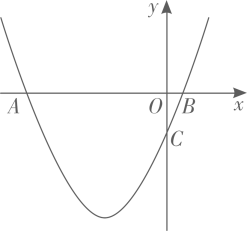
 2. 已知抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C , 点 在抛物线上,E是该抛物线对称轴上一动点.当 的值最小时, 的面积为 .3. 定义[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的一些结论:①当m≠0时,点(1,0)一定在函数的图象上;②当m>0时,函数图象截x轴所得的线段长度大于 ;③当m<0时,函数在 时,y随x的增大而减小;④当m>0,若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,则 ,正确的结论是.(填写序号)4. 已知二次函数 ( 是常数,且 )的图象的对称轴为直线 ,与 轴的一个交点为 ,与 轴的交点在 和 (不包括这两点)之间,则下列结论:① ;②一元二次方程 有两个不相等的实数根;③函数可取得最大值 ;④ .其中所有正确结论的序号是.5. 已知抛物线 过点 ,与 轴和直线 分别相交于点A、B,点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,若 ,则b的取值范围为.6. 在平面直角坐标系 中, , ,若抛物线 经过点A且与线段AB有两个不同的交点,则a的取值范围是 .7. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)
2. 已知抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C , 点 在抛物线上,E是该抛物线对称轴上一动点.当 的值最小时, 的面积为 .3. 定义[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的一些结论:①当m≠0时,点(1,0)一定在函数的图象上;②当m>0时,函数图象截x轴所得的线段长度大于 ;③当m<0时,函数在 时,y随x的增大而减小;④当m>0,若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,则 ,正确的结论是.(填写序号)4. 已知二次函数 ( 是常数,且 )的图象的对称轴为直线 ,与 轴的一个交点为 ,与 轴的交点在 和 (不包括这两点)之间,则下列结论:① ;②一元二次方程 有两个不相等的实数根;③函数可取得最大值 ;④ .其中所有正确结论的序号是.5. 已知抛物线 过点 ,与 轴和直线 分别相交于点A、B,点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,若 ,则b的取值范围为.6. 在平面直角坐标系 中, , ,若抛物线 经过点A且与线段AB有两个不同的交点,则a的取值范围是 .7. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)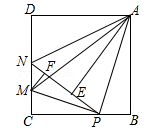
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为;
⑤当△ABP≌△ADN时,BP=.
8. 某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道CD=5 cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球",路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB=cm 9. 对称轴为 的抛物线 如图所示,与x 轴分别交于点 , , ,有下列五个结论:① ;② ;③ (t为实数);④当 时,y随x增大而增大;⑤若方程 的两个实数根分别为 , ,且 ,则 , .其中结论错误的是 .
9. 对称轴为 的抛物线 如图所示,与x 轴分别交于点 , , ,有下列五个结论:① ;② ;③ (t为实数);④当 时,y随x增大而增大;⑤若方程 的两个实数根分别为 , ,且 ,则 , .其中结论错误的是 .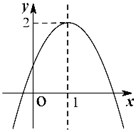 10. 下列关于二次函数 ( 为常数)的结论:
10. 下列关于二次函数 ( 为常数)的结论:①该函数的图象与函数 的图象的对称轴相同;
②该函数的图象的顶点在函数 的图象上;
③该函数的图象与 轴有交点时, ;
④点 与点 在该函数的图象上.
若 , ,则 .
其中正确的结论是(填写序号).
11. 已知函数 与y轴交于点C , 顶点为D . 直线 交x轴于点E , 点F在直线 上,且橫坐标为4,现在,将抛物线沿其对称轴上下平移,使抛物线与线段 总有公共点.抛物线向上最多可以平移个单位长度,向下最多可以平移个单位长度.12. 已知二次函数 ( )图象的对称轴为直线 ,部分图象如图所示,下列结论中:① ;② ;③ ;④若 为任意实数,则有 ;⑤当图象经过点 时,方程 的两根为 , ,则 ,其中正确的结论有 . 13. 如图所示,抛物线 与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为.
13. 如图所示,抛物线 与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为.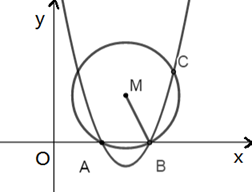 14. 如图,在平面直角坐标系中, A(-3, 0), B(0, 1),形状相同的抛物线Cn(n=1,2,3,4,×××)的顶点在直线 AB 上,其对称轴与 x 轴的交点的横坐标依次为 2,3,5,8,13,×××根据上述规律,抛物线C8的顶点坐标为.
14. 如图,在平面直角坐标系中, A(-3, 0), B(0, 1),形状相同的抛物线Cn(n=1,2,3,4,×××)的顶点在直线 AB 上,其对称轴与 x 轴的交点的横坐标依次为 2,3,5,8,13,×××根据上述规律,抛物线C8的顶点坐标为. 15. 抛物线 与线段 有两个不同的交点,已知 , ,则 的取值范围是 .16. 如图,将矩形 置于平面直角坐标系中,B点坐标为 ,点D为BC上一点,且 ,连接AD,将 沿AD折叠,压平,使B点的对应点E落在坐标平面内.若抛物线 ( ,a为常数)的顶点落在 的内部(不含边界),则a的取值范围为.
15. 抛物线 与线段 有两个不同的交点,已知 , ,则 的取值范围是 .16. 如图,将矩形 置于平面直角坐标系中,B点坐标为 ,点D为BC上一点,且 ,连接AD,将 沿AD折叠,压平,使B点的对应点E落在坐标平面内.若抛物线 ( ,a为常数)的顶点落在 的内部(不含边界),则a的取值范围为. 17. 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是.
17. 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是.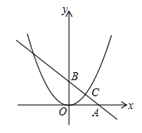 18. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .19. 某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为件(用含x的代数式表示).
18. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .19. 某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为件(用含x的代数式表示).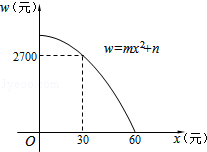 20. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元,则平均每次降价的百分率是.21. 某商品原价为180元,连续两次提价后售价为300元,且每次提价的百分率相等,设每次提价的百分率为x,依题意可列方程.22. 右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m。
20. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元,则平均每次降价的百分率是.21. 某商品原价为180元,连续两次提价后售价为300元,且每次提价的百分率相等,设每次提价的百分率为x,依题意可列方程.22. 右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m。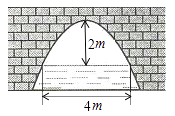 23. 如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升小时水位能由正常水位到达拱桥顶.
23. 如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升小时水位能由正常水位到达拱桥顶. 24. 如图(1)是一个横断面为抛物线形状的拱桥,水面在1时,拱顶(拱桥洞的最高点)离水面3米,水面宽4米.如果按图(2)建立平面直角坐标系,那么抛物线的解析式是 .
24. 如图(1)是一个横断面为抛物线形状的拱桥,水面在1时,拱顶(拱桥洞的最高点)离水面3米,水面宽4米.如果按图(2)建立平面直角坐标系,那么抛物线的解析式是 . 25. 为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是米.
25. 为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是米. 26. 一名运动员在平地上推铅球,铅球出手时离地面的高度为米,出手后铅球离地面的高度y(米)与水平距离x(米)之间的函数关系式为 , 当铅球离地面的高度最大时,与出手点水平距离为5米,则该运动员推铅球的成绩为米.27. 圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为米.
26. 一名运动员在平地上推铅球,铅球出手时离地面的高度为米,出手后铅球离地面的高度y(米)与水平距离x(米)之间的函数关系式为 , 当铅球离地面的高度最大时,与出手点水平距离为5米,则该运动员推铅球的成绩为米.27. 圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为米.
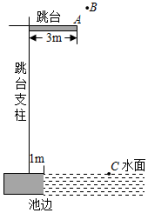
 28. 中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面m.
28. 中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面m.