备考浙教版中考数学题型专项训练反比例函数解答题专练

试卷更新日期：2022-05-23 类型：三轮冲刺

进入出卷网下载

一、综合题

1. 通过构造恰当的图形，可以对线段长度、图形面积大小等进行比较，直观地得到一些不等关系或最值，这是“数形结合”思想的典型应用．

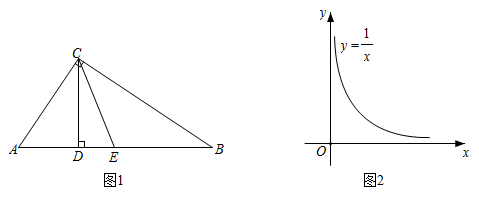(1)、【理解】
如图1， $A C ⊥ B C ， C D ⊥ A B$ ，垂足分别为C、D，E是 $A B$ 的中点，连接 $C E$ ．已知 $A D = a$ ， $B D = b (0 < a < b)$ ．
①分别求线段 $C E$ 、 $C D$ 的长（用含a、b的代数式表示）；
②比较大小： $C E$       ▲ $C D$ （填“＜”、“＝”或“＞”），并用含a、b的代数式表示该大小关系．

(2)、【应用】
如图2，在平面直角坐标系 $x O y$ 中，点M、N在反比例函数 $y = \frac{1}{x} (x > 0)$ 的图像上，横坐标分别为m、n．设 $p = m + n ， q = \frac{1}{m} + \frac{1}{n}$ ，记 $l = \frac{1}{4} p q$ ．
①当 $m = 1 ， n = 2$ 时， $l =$       ▲ ；当 $m = 3 ， n = 3$ 时， $l =$       ▲ ；
②通过归纳猜想，可得l的最小值是      ▲ ．请利用图2构造恰当的图形，并说明你的猜想成立．

查看试题解析
2. 如图，在平面直角坐标系中，四边形 $A B C D$ 是平行四边形， $A D = 6$ ，若 $O A$ 、 $O B$ 的长是关于x的一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根，且 $O A > O B$ .

(1)、求 $O A$ 、 $O B$ 的长.

(2)、若点E为x轴正半轴上的点，且 $S_{△ A O E} = \frac{16}{3}$ ，求经过D、E两点的直线解析式及经过点D的反比例函数的解析式，并判断 $△$ AOE与 $△$ AOD是否相似.

(3)、若点M在平面直角坐标系内，则在直线 $A B$ 上是否存在点F，使以A、C、F、M为顶点且 $A C$ 、 $A F$ 为邻边的四边形为菱形？若存在，写出F点的坐标，若不存在，请说明理由.

查看试题解析
3. 如图，一次函数y＝ax﹣1的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于A，B两点，与x轴交于点C，与y轴交于点D，已知OA＝ $\sqrt{10}$ ， tan∠AOC＝ $\frac{1}{3}$

(1)、求a，k的值及点B的坐标；

(2)、观察图象，请直接写出不等式ax﹣1≥ $\frac{k}{x}$ 的解集；

(3)、在y轴上存在一点P，使得△PDC与△ODC相似，请你求出P点的坐标．

查看试题解析
4. 如图，矩形ABCD的两边AD、AB的长分别为3、8，边BC落在x轴上，E是DC的中点，连接AE．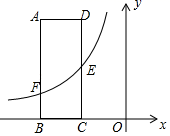

(1)、若点B坐标为（﹣6，0），求直线AE的表达式；

(2)、反比例函数y＝ $\frac{m}{x}$ （x＜0）的图象经过点E，与AB交于点F，若AF﹣AE＝2，求反比例函数的表达式；

(3)、在（2）的条件下，连接矩形ABCD两对边AD与BC的中点M、N，设线段MN与反比例函数图象交于点P，将线段MN沿x轴向右平移n个单位，若MP＜NP，直接写出n的取值范围．

查看试题解析
5. 如图，过原点的直线y＝2x交反比例函数y₁＝ $\frac{2}{x}$ 于B点，交反比例函数y₂＝ $\frac{k}{x}$ 于C点，且OB＝BC，A点横坐标为4且为y₁＝ $\frac{2}{x}$ 上一点，过B点作BD⊥x轴，垂足为点D.

(1)、求反比例函数y₂＝ $\frac{k}{x}$ 与直线AD的解析式

(2)、是否反比例函数y₂＝ $\frac{k}{x}$ 图象在第一象限内存在一点P，使得S_△ABP＝ $\frac{5}{11}$ S_{四边形ADBP} ，若存在，求出P点坐标；若不存在，请说明理由.

(3)、若动点Q在图象y₂＝ $\frac{k}{x}$ 上，在平面内是否存在点H，使得A、B、Q、H四点能组成以AB为边的矩形？若存在，请直接写出H点的坐标；若不存在，请说明理由.

查看试题解析

6. 为了探索函数y＝x+

\frac{1}{x}

（x＞0）的图象与性质，我们参照学习函数的过程与方法.

列表：

x	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	5	…
y	…	$\frac{17}{4}$	$\frac{10}{3}$	$\frac{5}{2}$	2	$\frac{5}{2}$	$\frac{10}{3}$	$\frac{17}{4}$	$\frac{26}{5}$	…

描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图1所示：

(1)、如图1，观察所描出点的分布，用一条光滑曲线将点顺次连接起来，作出函数图象；

(2)、已知点（x₁ ， y₁），（x₂ ， y₂）在函数图象上，结合表格和函数图象，回答下列问题：

若0＜x₁＜x₂≤1，则y₁y₂；若1＜x₁＜x₂ ，则y₁y₂；

若x₁•x₂＝1，则y₁y₂（填“＞”，“＝”或“＜”）.

(3)、某农户要建造一个图2所示的长方体形无盖水池，其底面积为1平方米，深为1米.已知底面造价为1千元/平方米，侧面造价为0.5千元/平方米.设水池底面一边的长为x米，水池总造价为y千元.

①请写出y与x的函数关系式；

②若该农户预算不超过3.5千元，请直接写出水池底面一边的长x的取值范围.

查看试题解析

7. 如图，一次函数 $y = \frac{1}{2} x + 1$ 的图象与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $C$ ，与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于B，D两点，且AC=BC.

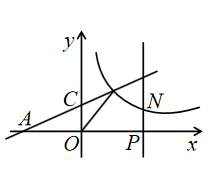(1)、求反比例函数的解析式；

(2)、已知 $P$ 是 $x$ 轴正半轴上一点，作 $P M ⊥ x$ 轴交直线 $A B$ 于点 $M$ ，交双曲线于点 $N$ ，当 $O$ ， $C$ ， $M$ ， $N$ 为顶点的四边形为平行四边形时，请写出点 $P$ 的坐标.

查看试题解析
8. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于 $A 、 B$ 两点，其中点 $A$ 的坐标为 $(- 1 ， 4)$ ，点B的坐标为 $(4 ， n)$ ．

(1)、求这两个函数的表达式；

(2)、根据图象，直接写出满足 $k x + b > \frac{k_{2}}{x}$ 的 $x$ 的取值范围；

(3)、若点 $P$ 在 $y$ 轴上，使得 $S_{△ A B P} = 10$ ，请直接写出点 $P$ 的坐标．

查看试题解析
9. 如图，在平面直角坐标系中， $O$ 为坐标原点，点 $B$ 在 $x$ 轴正半轴上，四边形 $O A C B$ 为平行四边形， $c o s ∠ A O B = \frac{\sqrt{3}}{3}$ ，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象在第一象限内过点 $A$ ，且经过 $B C$ 边的中点 $F$ ，连接 $A F$ ， $O F$ ．

(1)、当 $O A = \sqrt{3}$ 时，求反比例函数的表达式；

(2)、在（1）的条件下，求点 $F$ 的坐标；

(3)、证明： $Δ O A F ∽ Δ A F C$ ．

查看试题解析
10. 如图，在平面直角坐标系中，点 $A (- m ， m)$ 在反比例函数 $y = \frac{- m^{2}}{x} (x < 0)$ 的图象上，点 $C$ 在反比例函数 $y = \frac{- 2 m^{2}}{x} (x > 0)$ 的图象上，矩形 $A B C D$ 与坐标轴的交点分别为 $H$ ， $E$ ， $F$ ， $G$ ， $A B // y$ 轴，连接 $A E$ ， $A F$ ，分别交坐标轴于点 $M$ ， $N$ ，连接 $M N$ .

(1)、求证： $∠ E A F$ 为定值；

(2)、若 $M$ 为 $O H$ 的中点，求 $\tan ∠ A N M$ .

查看试题解析
11. 已知一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象在第一象限交于点 $A$ ，与 $x$ 轴交于点 $B$ ，与 $y$ 轴交于点 $C (0 ， - 8)$ ，若 $C B = A B$ ，且 $S_{Δ O A B} = 8$ ．

(1)、求反比例函数与一次函数的解析式；

(2)、直接写出 $k x + b - \frac{m}{x} < 0$ 的解集；

(3)、若点 $P$ 为 $y$ 轴上一点，求使 $∠ A P B = 90 °$ 的点 $P$ 的坐标．

查看试题解析
12. 如图，抛物线L： $y = - \frac{1}{2} (x - t) (x - t + 4)$ （常数t＞0）与x轴从左到右的交点为B，A，过线段OA的中点M作MP⊥x轴，交双曲线 $y = \frac{k}{x} (k > 0 ， x > 0)$ 于点P，且OA·MP=12.

(1)、求k值；

(2)、当t=1时，求AB长，并求直线MP与L对称轴之间的距离；

(3)、把L在直线MP左侧部分的图象（含与直线MP的交点）记为G，用t表示图象G最高点的坐标；

(4)、设L与双曲线有个交点的横坐标为x₀ ，且满足4≤x₀≤6，通过L位置随t变化的过程，直接写出t的取值范围.

查看试题解析
13. 如图

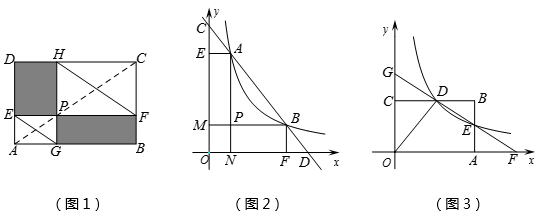(1)、方法体验：
如图1，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H，容易证明四边形PEDH和四边形PFBG是面积相等的矩形，分别连结EG，FH.

①根据矩形PEDH和矩形PFBG面积相等的关系，那么PE·PH= ▲ .

②求证：EG∥FH.

(2)、方法迁移：
如图2，已知直线 $y = a x + b (a \neq 0)$ 分别与x轴，y轴交于D，C两点，

与双曲线 $y = \frac{k}{x}$ 交于A，B两点. 求证：AC=BD.

(3)、知识应用：
如图3，反比例函数 $y = \frac{k}{x}$ （x＞0）的图象与矩形ABCO的边BC交于点D，与边AB交于点E，直线DE与x轴，y轴分别交于点F，G . 若矩形ABCO的面积为10，△ODG与△ODF的面积比为3：5，则k=.

查看试题解析

14. 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．我们对函数

y = \frac{a x}{(x - 1)^{2} + b}

图象与性质进行探究，下表是该函数y与自变量x的几组对应值，请解答下列问题：

…

$- 3$

$- \frac{5}{2}$

$- 2$

$- \frac{3}{2}$

$- 1$

$- \frac{1}{2}$

$\frac{1}{2}$

$1$

$\frac{3}{2}$

$2$

$\frac{5}{2}$

$3$

…

$\frac{18}{17}$

$\frac{60}{53}$

$\frac{36}{29}$

$\frac{6}{5}$

$\frac{12}{13}$

$- \frac{12}{5}$

$- 6$

$- \frac{36}{5}$

$- \frac{60}{13}$

$- \frac{18}{5}$

…

(1)、求该函数的解析式，并写出自变量x的取值范围．

(2)、表中m的值为， n的值为．

(3)、在如图所示的平面直角坐标系中，画出该函数的图象，并写出该函数的一条性质；

(4)、直接写出关于x的不等式

\frac{a x}{(x - 1)^{2} + b} \leq - \frac{12}{5} x - \frac{6}{5}

的解集是．（如果取近似值，误差不超过0.2）．

查看试题解析

15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，顶点 $A$ ， $B$ 都在反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上，直线 $B C ⊥ x$ 轴，垂足为 $D$ ，连接 $O B$ ， $O C$ ．

(1)、若 $O B = 4$ ， $∠ B O D = 60 °$ ，求 $k$ 的值；

(2)、若 $t a n ∠ A B C = 2$ ，求直线 $O C$ 的解析式．

查看试题解析
16. 如图，一次函数 $y = 2 x - b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $A$ 、 $B$ 两点，与 $x$ 轴、 $y$ 轴分别交于 $C$ 、 $D$ 两点，且点 $A$ 的坐标为 $(3 ， 2)$ .

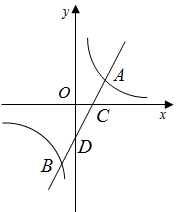(1)、求一次函数和反比例函数的表达式.

(2)、求 $△ A O B$ 的面积.

(3)、点 $P$ 为反比例函数图象上的一个动点， $P M ⊥ x$ 轴于 $M$ ，是否存在以 $P$ 、 $M$ 、 $O$ 为顶点的三角形与 $△ C O D$ 相似，若存在，直接写出 $P$ 点的坐标，若不存在，请说明理由.

查看试题解析
17. 知识背景
当a＞0且x＞0时，因为（ $\sqrt{x}$ ﹣ $\frac{\sqrt{a}}{\sqrt{x}}$ ）²≥0，所以x﹣2 $\sqrt{a}$ + $\frac{a}{x}$ ≥0，从而x+ $\frac{a}{x} \geq 2 \sqrt{a}$ （当x= $\sqrt{a}$ 时取等号）.

设函数y=x+ $\frac{a}{x}$ （a＞0，x＞0），由上述结论可知：当x= $\sqrt{a}$ 时，该函数有最小值为2 $\sqrt{a}$ .

应用举例

已知函数为y₁=x（x＞0）与函数y₂= $\frac{4}{x}$ （x＞0），则当x= $\sqrt{4}$ =2时，y₁+y₂=x+ $\frac{4}{x}$ 有最小值为2 $\sqrt{4}$ =4.

解决问题

(1)、已知函数为y₁=x+3（x＞﹣3）与函数y₂=（x+3）²+9（x＞﹣3），当x取何值时， $\frac{y_{2}}{y_{1}}$ 有最小值？最小值是多少？

(2)、已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001.若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租货使用成本最低？最低是多少元？

查看试题解析
18. 如图，在平面直角坐标系中，函数 $y = \frac{k}{x}$ （ $x > 0$ ，是常数）的图像经过A(2，6)，B(m，n)，其中m>2.过点A作 $x$ 轴垂线，垂足为C，过点 $B$ 作轴垂线，垂足为 $D$ ，AC与BD交于点E，连结AD， $D C$ ，CB.

(1)、若 $△ A B D$ 的面积为3，求m的值和直线 $A B$ 的解析式；

(2)、求证： $\frac{D E}{C E} = \frac{B E}{A E}$ ；

(3)、若AD//BC ，求点B的坐标 .

查看试题解析
19. 如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ $\sqrt{3}$ ，1）在反比例函数 $y = \frac{k}{x}$ 的图象上．

(1)、求反比例函数 $y = \frac{k}{x}$ 的表达式；

(2)、在x轴的负半轴上存在一点P，使得S_△_AOP= S_△_AOB ，求点P的坐标；

(3)、若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．

查看试题解析
20. 一辆客车从甲地出发前往乙地，平均速度v(千米／小时)与所用时间t(小时)的函数关系如图所示，其中60≤v≤120．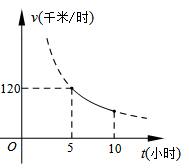

(1)、直接写出v与t的函数关系式；

(2)、若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶20千米，3小时后两车相遇．
①求两车的平均速度；

②甲、乙两地问有两个加油站A，B，它们相距200千米，当客车进入B加油站时，货车恰好进入A加油站(两车加油的时间忽略不计)，求甲地与B加油站的距离．

查看试题解析
21. 【阅读理解】对于任意正实数a、b，因为 ${(\sqrt{a} - \sqrt{b})}^{2}$ ≥0，所以 $a -$ $2 \sqrt{a b} + b$ ≥0，所以 $a + b$ ≥2 $\sqrt{a b}$ ，只有当 $a = b$ 时，等号成立．
【获得结论】在 $a + b$ ≥2 $\sqrt{a b}$ （a、b均为正实数）中，若 $a b$ 为定值 $p$ ，则 $a + b$ ≥2 $\sqrt{p}$ ，只有当 $a = b$ 时， $a + b$ 有最小值2 $\sqrt{p}$ ．

(1)、根据上述内容，回答下列问题：若 $m$ >0，只有当 $m$ =时， $m + \frac{1}{m}$ 有最小值．

(2)、【探索应用】如图，已知A（－3，0），B（0，－4），P为双曲线 $y = \frac{12}{x}$ （ $x$ ＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

查看试题解析
22. 如图，平面直角坐标系中，点C在x轴上，点A的横坐标是1，以OA ， OC为邻边作 $▱ A B C O$ ，点D是BC的中点，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点A ，点D ．

(1)、求点B的坐标（用含k的代数式表示）；

(2)、连接AD ，若AB＝AD ，求k的值．

查看试题解析
23. 如图，在平面直角坐标系xOy中，菱形ABCD的顶点B的坐标为（1，0），顶点C的坐标为（4，2），对角线AC∥x轴，边AB所在直线y₁＝ax+b与反比例函数y₂＝ $\frac{k}{x}$ （k＜0）的图象交于A，E两点；

(1)、求y₁和y₂的函数解析式；

(2)、当y₁＞y₂时，求x的取值范围；

(3)、点P是x轴上一动点，当△PAC是以AC为斜边的直角三角形时，请直接写出点P的坐标.

查看试题解析
24. 如图，在平面直角坐标系中，正六边 $A B C D E F$ 的对称中心 $P$ 在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，边 $C D$ 在 $x$ 轴上，点 $B$ 在 $y$ 轴上．已知 $C D = 2$ ．

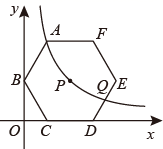(1)、点 $A$ 是否在该反比例函数的图象上？请说明理由．

(2)、若该反比例函数图象与 $D E$ 交于点 $Q$ ．求点 $Q$ 的横坐标．

查看试题解析
25. 如图，在平面直角坐标系xOy中，双曲线y₁＝ $\frac{k}{x}$ 与直线y₂＝mx＋n交于点A ， E ， AE交x轴于点C ，交y轴于点D ， $A B ⊥ x$ 轴于点B，C为OB中点．若D点坐标为（0，﹣2），且S_△AOD＝4

(1)、求双曲线与直线AE的解析式；

(2)、写出E点的坐标；

(3)、观察图象，直接写出y₁≥y₂时x的取值范围．

查看试题解析
26. 跳台滑雪是北京冬奥会的比赛项目之一.下图是某跳台滑雪场地的截面示意图. 平台AB长1米（即AB=1），平台AB距地面18米.以地面所在直线为x轴，过点B垂直于地面的直线为y轴，取1米为单位长度，建立平面直角坐标系.已知滑道对应的函数为 $y = \frac{k}{x} (x \geq 1)$ .运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落过程中的某位置（忽略空气阻力）.设运动员飞出时间为t秒，运动员与点A的竖直距离为h米，运动员与点A的水平距离为l米.经实验表明：h=6t² ， l=vt.

(1)、求k的值；

(2)、当v=5，t=1时，通过计算判断运动员是否落在滑道上；

(3)、若运动员甲、乙同时从A处飞出，已知甲离开点A的速度是5米/秒.当甲距x轴4.5米时，乙恰好位于甲右侧4.5米的位置，求t的值与运动员乙离开A的速度.

查看试题解析

27. 某同学设计了如下杠杆平衡实验：如图，取一根长65cm的质地，均匀木杆，用细绳绑在木杆的中点O处并将其吊起来，在中点的左侧，距离中点20cm处挂一个重9N的物体，在中点的右侧，用一个弹簧测力计向下拉，使木杆保持平衡（动力×动力臂＝阻力×阻力臂），改变弹簧测力计与中点O的距离L（单位：cm），观察弹簧测力计的示数F（单位：N）. 通过实验，得到下表数据：

	第1组	第2组	第3组	第4组	第5组
L/cm	20	24	25	28	30
F/N	9	7.5	10	6

(1)、你认为表中哪组数据是明显错误的.

(2)、在已学过的函数中选择合适的模型，求F关于L的函数表达式.

(3)、若弹簧测力计的量程是10N，求L的取值范围.

查看试题解析

28. 厨余垃圾无公害化、高效化处理是破解“日益严重的垃圾包围城市的困境”的重要手段之一.某科研团队在自然界中找到了两种“吞噬细菌甲，乙”，并进行实验室繁殖.通过研究，科研人员发现：等数量的吞噬细菌甲、乙分解单位体积内的厨余垃圾的速率v（单位： $mol / min$ ）与环境温度T（单位：℃）存在如图所示的函数关系，分段函数 $C_{2}$ 对应吞噬细菌甲、分段函数 $C_{1}$ 对应吞噬细菌乙（ $C_{1}$ 与 $C_{2}$ 的图象中，曲线部分是双曲线，其余均是直线）.

(1)、根据图中给出的数据，求函数 $C_{1}$ ， $C_{2}$ 的函数解析式；

(2)、在测试中，科研人员又发现：若吞噬细菌甲、乙共存，则总分解速率v将会发生改变，对应的函数曲线为 $C_{3}$ ，其中，线段 $O D$ 是 $∠ A O C$ 的角平分线，求线段 $O D$ 对应的函数解析式.

查看试题解析

29. 汛期到来，山洪暴发，下表记录了某水库

20 h

内水位的变化情况，其中

x

表示时间（单位：

h

），

y

表示水位高度（单位：

m

），当

x = 8

（

h

）时，达到警戒水位，开始开闸放水.

$x / h$	0	2	4	6	8	10	12	14	16	18	20
$y / m$	14	15	16	17	18	14.4	12	10.3	9	8	7.2

(1)、在给出的平面直角坐标系中，根据表格中的数据画出水位变化图象，并写出水位高出16米的时间

x

的取值范围 ▲ .（精确到0.1）

(2)、请分别求出开闸放水前和放水后最符合表中数据的函数解析式.

(3)、据估计，开闸放水后，水位的这种变化规律还会持续一段时间，预测何时水位达到

6 m

查看试题解析

30. 如图，小明想要用撬棍撬动一块大石头，已知阻力为 $1200 N$ ，阻力臂长为 $0 .5m$ .设动力为y（N），动力臂长为x（m）.（杠杆平衡时，动力×动力臂＝阻力×阻力臂，图中撬棍本身所受的重力略去不计.）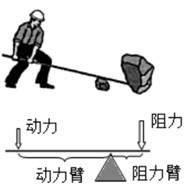

(1)、求y关于x的函数表达式.

(2)、当动力臂长为 $1 .5m$ 时，撬动石头至少需要多大的力？

(3)、小明若想使动力不超过 $300N$ ，在动力臂最大为 $1 .8m$ 的条件下，他能否撬动这块石头？请说明理由.

查看试题解析

备考浙教版中考数学题型专项训练 反比例函数解答题专练

一、综合题

备考浙教版中考数学题型专项训练反比例函数解答题专练