备考浙教版中考数学题型专项训练数与式解答题专练-在线组卷题库

1. 若一个整数能表示成 a²+b²（a，b 是整数）的形式，则称这个数为“完美数”.例如，13＝3²+2² ，所以 13 是“完美数”．再如，M＝x²+2xy+2y²＝（x+y）²+y²（x，y 是整数），所以 M 也是“完美数”．

(1)、请直接写出一个小于 10 的“完美数”，这个“完美数”是；

判断：34（请填写“是”或“不是”）“完美数”；

(2)、已知S＝x²+4y²+4x﹣12y+k（x，y是整数，k 是常数），要使S为“完美数”，试求出符合条件的一个 k 值，并说明理由．

(3)、如果数 m，n 都是“完美数”，m≠n，试说明

\frac{{(m + n)}^{2} - {(m - n)}^{2}}{4}

也是“完美数”．

查看试题解析

2. 若

x

满足

(9 - x) (x - 4) = 4

，求

{(4 - x)}^{2} + {(x - 9)}^{2}

的值.

解：设 $9 - x = a ， x - 4 = b$ ，则 $(9 - x) (x - 4) = a b = 4 ， a + b = (9 - x) + (x - 4) = 5$ ，

∴ ${(9 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$

请仿照上面的方法求解下面问题：

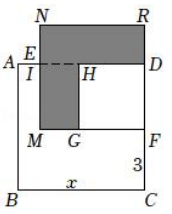(1)、若x满足(x-10) (x-20）=15，求(x -10)²+ (x-20)²的值；

(2)、已知正方形ABCD的边长为x，E，F分别是AD，DC上的点，且AE=1，CF=3，长方形EMFD的面积是48，分别以MF，DF作正方形MFRN和正方形GFDH，求阴影部分的面积.

查看试题解析

3. 问题提出

我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小．例如：

对于任意两个代数式M，N的大小比较，有下面的方法：

当M－N＞0时，M ＞N；

当M－N＝0时，M＝N；

当M－N＜0时，M ＜N.

反过来也成立. 因此，我们把这种比较两个代数式大小的方法叫做“作差法”．

对于比较两个正数a，b的大小，我们还可以用它们的平方进行比较：

∵a²－b²＝（a＋b）（a－b），a＋b＞0，

∴（a²－b²）与（a－b）的符号相同.

当a²－b²＞0时，a－b＞0，得a＞b；

当a²－b²＝0时，a－b＝0，得a＝b；

当a²－b²＜0时，a－b＜0，得a＜b．

问题解决

(1)、课堂上，老师让同学们制作几种几何体，张丽同学用了3张A4纸，7张B5纸；李明同学用了2张A4纸，8张B5纸. 设每张A4纸的面积为x，每张B5纸的面积为y，且x＞y，张丽同学的用纸总面积为S₁ ，李明同学的用纸总面积为S₂. 回答下列问题：

①S₁＝ ▲ （用含x，y的代数式表示）；

S₂＝ ▲ （用含x，y的代数式表示）；

②试比较谁的用纸总面积更大？

(2)、如图1所示，要在燃气管道l上修建一个泵站，向A，B两镇供气，已知A，B到l的距离分别是3km，4km（即AC＝3km，BE＝4km），AB＝x km，现设计两种方案：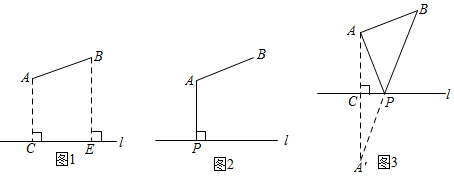

方案一：如图2所示，AP⊥l于点P，泵站修建在点P处，该方案中管道长度a₁=AB+AP.

方案二：如图3所示，点A′与点A关于l对称，A′B与l相交于点P，泵站修建在点P处，该方案中管道长度a₂＝AP+BP.

①在方案一中，a₁＝ ▲ km（用含x的代数式表示）；

②在方案二中，a₂＝ ▲ km（用含x的代数式表示）；

③请分析说明哪种方案铺设的输气管道较短？

(3)、甲、乙两位采购员同去一家饲料公司购买两次饲料，两次购买的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000kg，乙每次用去1000元，而不管购买多少饲料. 设两次购买的饲料单价分别为m元/kg和n元/kg（m，n是正数，且m≠n），试分析哪位采购员的购货方式合算？

查看试题解析

4. 给出如下定义：我们把有序实数对（a，b，c）叫做关于x的二次多项式

a x^{2} + b x + c

的特征系数对.把关于x的二次多项式

a x^{2} + b x + c

叫做有序实数对（a，b，c）的特征多项式.

(1)、关于x的二次多项式3x²+2x-1的特征系数对为；

(2)、求有序实数对（1，4，4）的特征多项式与有序实数对（1，－4，4）的特征多项式的乘积；

(3)、若有序实数对（p，q，－1）的特征多项式与有序实数对（m，n，－2）的特征多项式的乘积的结果为

2 x^{4} + x^{3} - 10 x^{2} - x + 2

；直接写出

(4 p - 2 q - 1) (2 m - n - 1)

的值为.

查看试题解析

5. 观察下列式子：

1 \times 3 + 1 = 2^{2}

，

2 \times 4 + 1 = 3^{2}

，

3 \times 5 + 1 = 4^{2}

……

(1)、请你根据上面式子的规律直接写出第7个式子：.

(2)、探索以上式子的规律，试写出第n个等式（n为正整数），并说明你结论的正确性.

查看试题解析

6. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个等式，例如图1，可以得到

{(a + b)}^{2} = a^{2} + 2 a b + b^{2}

这个等式，请解答下列问题：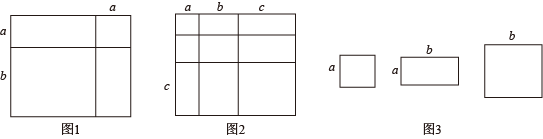

(1)、写出图2中所表示的数学等式；

(2)、利用（1）中的结论，解决下而的问题：

a + b + c = 10

，

a b + a c + b c = 35

，计算

a^{2} + b^{2} + c^{2}

的值：

(3)、小明同学用图3中x张边长为a的正方形，y张边长为b的正方形，z张长宽分别为a、b的长方形纸片拼出一个面积为

(2 a + b) (a + 4 b)

的长方形，则

x + y + z =

；

查看试题解析

7. 把代数式通过配凑等手段，得到完全平方式，再运用完全平方式的非负性这一性质增加问题的条件，这种解题方法通常被称为配方法。配方法在代数式求值、解方程、最值问题等问题中都有着广泛的应用.例如：若代数式

M = a^{2} - 2 a b + 2 b^{2} - 2 b + 2

，利用配方法求M的最小值；

$M = a^{2} - 2 a b + 2 b^{2} - 2 b + 2 = a^{2} - 2 a b + b^{2} + b^{2} - 2 b + 1 + 1 = {(a - b)}^{2} + {(b - 1)}^{2} + 1$ ，

∵ ${(a - b)}^{2} \geq 0$ ， ${(b - 1)}^{2} \geq 0$ ，

∴ $M = {(a - b)}^{2} + {(b - 1)}^{2} + 1 \geq 1$

∴当 $a = b = 1$ 时，代数式M有最小值1.

请根据上述材料解决下列问题：

(1)、在横线上添上一个常数项使之成为完全平方式：

a^{2} + 6 a +

；

(2)、若代数式

N = - \frac{1}{4} a^{2} + 2 a + 1

，求N的最大值；

(3)、已知

\frac{37}{9} a^{2} + 81 b^{2} = 36 a b + 4 a - 36

，求以a，b为边长的等腰三角形的周长.

查看试题解析

8. 数学教育家波利亚曾说：“对一个数学问题，改变它的形式，变换它的结构，直到发现有价值的东西，这是数学解题的一个重要原则”.

材料一：把根式 $\sqrt{x \pm 2 \sqrt{y}}$ 进行化简，若能找到两个数m、n，是 $m^{2} + n^{2} = x$ 且 $m n = \sqrt{y}$ ，则把 $x \pm 2 \sqrt{y}$ 变成 $m^{2} + n^{2} \pm 2 m n = {(m \pm n)}^{2}$ ，开方，从而使得 $\sqrt{x \pm 2 \sqrt{y}}$ 化简.

例如：化简 $\sqrt{3 + 2 \sqrt{2}}$

解：∵ $3 + 2 \sqrt{2} = 1 + 2 + 2 \sqrt{2} = 1^{2} + {(\sqrt{2})}^{2} + 2 \times 1 \times \sqrt{2} = {(1 + \sqrt{2})}^{2}$

∴ $\sqrt{3 + 2 \sqrt{2}} = \sqrt{{(1 + \sqrt{2})}^{2}} = 1 + \sqrt{2}$

材料二：在直角坐标系xOy中，对于点P（x，y）和Q（x，y'）给出如下定义：若 $y' = {\begin{array}{l} y ， (x \geq 0) \\ - y ， (x < 0) \end{array}$ ，则称Q点为P点的“横负纵变点”.例如点（3，2）的“横负纵变点”为（3，2），点（ $- 2$ ，5）的“横负纵变点”为（ $- 2$ ， $- 5$ ）.

请选择合适的材料解决下面的问题：

(1)、点（

\sqrt{2}

，

- \sqrt{3}

）的“横负纵变点”为；

(2)、化简：

\sqrt{7 + 2 \sqrt{10}}

；

(3)、已知a为常数（

1 \leq a \leq 2

），点M（

- \sqrt{2}

，m）且

m = \frac{1}{\sqrt{2}} (\sqrt{a + 2 \sqrt{a - 1}} + \sqrt{a - 2 \sqrt{a - 1}})

，点M'是点M的“横负纵变点”，求点M'的坐标.

查看试题解析

9. 如果一个两位数的个位数字是n，十位数字是m，那么我们可以把这个两位数简记为

\bar{m n}

，即

\bar{m n}

＝10m+n．如果一个三位数的个位数字是c，十位数字是b，百位数字是a，那么我们可以把这个三位数简记为

\bar{a b c}

，即

\bar{a b c}

＝100a+10b+c．

(1)、若一个两位数

\bar{m n}

满足

\bar{m n}

＝7m+5n，请求出m，n的数量关系并写出这个两位数．

(2)、若规定：对任意一个三位数

\bar{a b c}

进行M运算，得到整数M（

\bar{a b c}

）＝a³+b²+c．如：M（

\bar{321}

）＝3³+2²+1＝32．若一个三位数

\bar{5 x y}

满足M（

\bar{5 x y}

）＝132．求这个三位数．

(3)、已知一个三位数

\bar{a b c}

和一个两位数

\bar{a c}

，若满足

\bar{a b c}

＝6

\bar{a c}

+5c，请求出所有符合条件的三位数．

查看试题解析

10. 阅读材料：在处理分数和分式的问题时，有时由于分子大于分母，或分子的次数高于分母的次数，在实际运算时难度较大，这时，我们可将分数（分式）拆分成一个整数（整式）与一个真分数（真分式）的和（差）的形式，通过对它的简单分析来解决问题，我们称这种方法为分离常数法，此法在处理分式或整除问题时颇为有效.

将分式分离常数可类比假分数变形带分数的方法进行，如： $\frac{x^{2} - 2 x + 3}{x - 1} = \frac{x (x - 1) + x - 2 x + 3}{x - 1} = x +$ $\frac{- (x - 1) + 2}{x - 1} = x - 1 + \frac{2}{x - 1}$ ，这样，分式就拆分成一个分式 $\frac{2}{x - 1}$ 与一个整式 $x - 1$ 的和的形式.

根据以上阅读材料，解答下列问题：

(1)、若x为整数，

\frac{x + 6}{x + 4}

为负整数，可求得 x最大值= ；

(2)、利用分离常数法，求分式

\frac{2 x^{2} + 5}{x^{2} + 1}

的取值范围；

(3)、若分式

\frac{5 x^{2} + 9 x - 3}{x + 2}

拆分成一个整式与一个真分式（分子为整数）的和（差）的形式为：

5 m - 11 + \frac{1}{n - 6}

（整式部分对应等于

5 m - 11

，真分式部分对应等于

\frac{1}{n - 6}

）.

①用含x的式子表示出mn；

②随着x的变化， $m^{2} + n^{2} + m n$ 有无最小值？如有，最小值为多少？

查看试题解析

11. 如图，P是线段AB上不同于点A，B的一点，AB＝18cm，C，D两动点分别从点P，B同时出发，在线段AB上向左运动（无论谁先到达A点，均停止运动），点C的运动速度为1cm/s，点D的运动速度为2cm/s．

(1)、若AP＝PB，

①当动点C，D运动了2s时，AC＋PD＝cm；

②当C，D两点间的距离为5cm时，则运动的时间为s；

(2)、当点C，D在运动时，总有PD＝2AC，·

①求AP的长度；

②若在直线AB上存在一点Q，使AQ﹣BQ＝PQ，求PQ的长度．

查看试题解析

12. 滴滴快车是一种便捷的出行工具，计价规则如下表：

计费项目	里程费	时长费	远途费
单位	1.3元/公里	0.3元/分钟	0.4元/公里
注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为：行车里程10公里以内（含10公里）不收远途费，超过10公里的，超出部分每公里收0.4元．

(1)、若乘坐滴滴快车，行车里程为8公里，行车时间为15分钟，则需付车费元．

(2)、若乘坐滴滴快车，行车里程为20公里，行车时间为30分钟，则需付车费元．

(3)、若小明乘坐滴滴快车，行车里程为a公里，行车时间为b分钟，则小明应付车费多少元（用含a、b的代数式表示，并化简．）

查看试题解析

13. 对于有理数a、b定义一种新运算a⊗b＝

{\begin{array}{l} 3 a - 2 b (a \geq b) \\ a - \frac{2}{3} b (a < b) \end{array}

，如5⊗3＝3×5﹣2×3＝9，1⊗3＝1﹣

\frac{2}{3}

×3＝﹣1；请按照这个定义完成下列计算：

(1)、计算

①5⊗（﹣3）＝ ▲ ；

②（﹣5）⊗（﹣3）＝ ▲ ；

③若x⊗ $\frac{3}{2}$ ＝﹣3，求x`的值；

(2)、若A＝﹣2x³+

\frac{2}{3} x^{2}

﹣x+1，B＝﹣2x³+x²﹣x+

\frac{3}{2}

，且A⊗B＝﹣4，求3x³+

\frac{3}{2}

x+2的值；

(3)、若x和k均为正整数，且满足

(\frac{k}{3} x + k) \otimes (\frac{1}{3} x + 1) = \frac{4}{3}

x+12，求k的值．

查看试题解析

14. 已知a，b互为倒数，x，y互为相反数．

(1)、求式子2x+3ab+2y的值；

(2)、若2^b＝4，b^y＝8，求式子72a^y﹣x^b的值．

查看试题解析

15. 观察图，解答下列问题．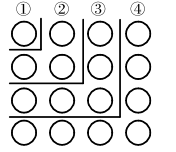

(1)、图中的圆圈被折线隔开分成六层，第一层有

1

个圆圈，第二层有

3

个圆圈，第三层有

5

个圆圈，…，第六层有

11

个圆圈．如果要你继续画下去，第

n

层有个圆圈．

(2)、某一层上有

65

个圆圈，这是第层．

(3)、数图中的圆圈个数可以有多种不同的方法．比如：前两层的圆圈个数和为

(1 + 3)

或

2^{2}

，由此得，

1 + 3 = 2^{2}

，同样：由前三层的圆圈个数和得：

1 + 3 + 5 = 3^{2}

，由前四层的圆圈个数和得：

1 + 3 + 5 + 7 = 4^{2}

， …根据上述规律，从

1

开始的

n

个连续奇数之和是多少？用

n

的代数式把它表示出来

(4)、运用（3）中的规律计算：

73 + 75 + 77 + \cdot \cdot \cdot + 153

．

查看试题解析

16. 对于一个各数位上的数字均不为0的三位自然数P，将它各个数位上的数字平方后再取其个位，得到三个新的数字；再将这三个新数字重新组合成三位数

\bar{x y z}

，当

| x + 2 z - y |

的值最小时，称此时的

\bar{x y z}

为自然数P的“忘忧数”，并规定忘忧值：

F (p) = {(x - y)}^{2} + z

，例如123，各数字平方后取个位分别为1，4，9，再重新组合为149，194，419，491，914，941，因为

| 1 + 2 \times 4 - 9 | = 0

最小，所以194是原三位数123的“忘忧数”，此时忘忧值

F (123) = {(1 - 9)}^{2} + 4 = 68

．

(1)、求235的“忘忧数”和

F (235)

的值；

(2)、一个三位正整数，从左向右它的前两个数字组成的两位数能被2除余1，它本身能被3除余2，则称这样的三位数为“常余数”，例如257，前两位数“25”被2除余1，“257”被3除余2，所以257是“常余数”．若一个小于200且各数位上的数字均不为0的“常余数”记为t，它的各位数字之和再加1为一个完全平方数，求“常余数”t的忘忧值

F (t)

的最大值．

查看试题解析

17. 在平面直角坐标系

x O y

中，对于任意两点

P_{1} (x_{1}

，

y_{1})

与

P_{2} (x_{2}

，

y_{2})

的“非常距离”，给出如下定义：

若 $| x_{1} - x_{2} | ⩾ | y_{1} - y_{2} |$ ，则点 $P_{1}$ 与点 $P_{2}$ 的“非常距离”为 $| x_{1} - x_{2} |$ ；

若 $| x_{1} - x_{2} | < | y_{1} - y_{2} |$ ，则点 $P_{1}$ 与点 $P_{2}$ 的“非常距离”为 $| y_{1} - y_{2} |$ .

例如：点 $P_{1} (1 ， 2)$ ，点 $P_{2} (3 ， 5)$ ，因为 $| 1 - 3 | < | 2 - 5 |$ ，所以点 $P_{1}$ 与点 $P_{2}$ 的“非常距离”为 $| 2 - 5 | = 3$ ，也就是图1中线段 $P_{1} Q$ 与线段 $P_{2} Q$ 长度的较大值(点 $Q$ 为垂直于 $y$ 轴的直线 $P_{1} Q$ 与垂直于 $x$ 轴的直线 $P_{2} Q$ 交点).

(1)、已知点

A (- \frac{1}{2}

，

0)

，

B

为

y

轴上的一个动点，

①若点 $A$ 与点 $B$ 的“非常距离”为2，写出一个满足条件的点 $B$ 的坐标；

②直接写出点 $A$ 与点 $B$ 的“非常距离”的最小值；

(2)、已知

C

是直线

y = \frac{3}{4} x + 3

上的一个动点，

①如图2，点 $D$ 的坐标是 $(0 ， 1)$ ，求点 $C$ 与点 $D$ 的“非常距离”的最小值及相应的点 $C$ 的坐标；

②如图3， $E$ 是以原点 $O$ 为圆心，1为半径的圆上的一个动点，求点 $C$ 与点 $E$ 的“非常距离”的最小值及相应的点 $E$ 与点 $C$ 的坐标.

查看试题解析

18. 材料一：对于一个四位数

n

，若满足千位数字与十位数字的和等于百位数字与个位数字的和，则称这个数为“间位等和数”，例如：

$n = 5247$ ， ∵ $5 + 4 = 2 + 7 = 9$ ， ∴5247是“间位等和数”；

$n = 3145$ ， ∵ $3 + 4 \neq 1 + 5$ ， ∴3145不是“间位等和数”

材料二：将一个四位数 $n$ 千位上的数字与百位上的数字对调，十位上的数字与个位上的数字对调后可以得到一个新的四位数 $m$ ，记 $F (n) = \frac{n - m}{99}$ .例如 $n = 5247$ ，对调千位上的数字与百位上的数字及十位上的数字与个位上的数字得到2574，所以 $F (5247) = \frac{5247 - 2574}{99} = 27$ .

(1)、判断3564和1572是否为“间位等和数”，并说明理由；

(2)、若

s

和

t

都是“间位等和数”，其中

s = 100 a + b + 5240

，

t = 1000 x + 10 y + 312

（

1 \leq a \leq 7

，

1 \leq b \leq 9

，

1 \leq x \leq 9

，

1 ≤ y ≤ 8

且

a

，

b

，

x

，

y

均为整数），规定：

k = \frac{F (t)}{F (s)}

，若

F (s) - 2 F (t) = 9

，求

k

的最小值.

查看试题解析

19. 对于四个数“-8，-2，1，3”及四种运算“＋，－，×，÷”，列算式解答：

(1)、求这四个数的和；

(2)、在这四个数中选出两个数，使得两数差的结果最小；

(3)、在这四个数中选出三个数，在四种运算中选出两种，组成一个算式，可以带括号，使运算结果等于没选的那个数．

查看试题解析

20. 对于二次函数

y = x^{2} - 4 x + 3

和一次函数

y = - x + 1

，我们把

y = t (x^{2} - 4 x + 3) + (1 - t) (- x + 1)

称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线E.现有点A(1，0)和抛物线E上的点B(2，n)，请完成下列任务：

（尝试）

(1)、当t=2时，抛物线

y = t (x^{2} - 4 x + 3) + (1 - t) (- x + 1)

的顶点坐标为

(2)、判断点A是否在抛物线E上；

(3)、求n的值.

（发现）通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线E总过定点，定点的坐标 ▲ .

（应用）二次函数 $y = - 3 x^{2} + 5 x - 2$ 是二次函数 $y = x^{2} - 4 x + 3$ 和一次函数 $y = - x + 1$ 的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由.

查看试题解析

21. 阅读材料：

《见微知著》谈到：从一个简单的经典问题出发，从特殊到一般，由简单到复杂，从部分到整体，由低维到高维，知识与方法上的类比是探索发展的重要途径，是思想阀门发现新问题、新结论的重要方法.

例如：已知 $x y = 1$ ，求 $\frac{1}{1 + x} + \frac{1}{1 + y}$ 的值.

解：原式 $= \frac{x y}{x y + x} + \frac{1}{1 + y} = \frac{y}{y + 1} + \frac{1}{1 + y} = \frac{y + 1}{y + 1} = 1$ .

问题解决：

(1)、已知

x y = 1

.

①代数式 $\frac{1}{1 + x^{2}} + \frac{1}{1 + y^{2}}$ 的值为 ▲ ；

②求证： $\frac{1}{1 + x^{2021}} + \frac{1}{1 + y^{2021}} = 1$ .

(2)、若x满足

{(2021 - x)}^{2} + {(2020 - x)}^{2} = 4043

，求

(2021 - x) (2020 - x)

的值.

查看试题解析

22. “字母表示数”的系统化阐述是由16世纪法国数学家韦达提出的，被后人称为从“算术”到“代数”的一次飞跃，从而大大推动了数学的发展．经过初中三年数学的学习，我们知道了用字母表示数可以分析从特殊到一般的数学规律，字母与数一样，也可以参与运算．请同学们观察下列等式：

第1个等式： $1 \times 3 \times 5 \times 7 + 16 = 11^{2}$ ；

第2个等式： $2 \times 4 \times 6 \times 8 + 16 = 20^{2}$ ；

第3个等式： $3 \times 5 \times 7 \times 9 + 16 = 31^{2}$ ；

第4个等式： $4 \times 6 \times 8 \times 10 + 16 = 44^{2}$ ；

第5个等式： $5 \times 7 \times 9 \times 11 + 16 = 59^{2}$ ；

……

按照以上规律，解答下列问题：

(1)、写出第6个等式和第7个等式；

(2)、用字母

n

表示第

n

个等式（其中

n

为正整数)；

(3)、若

x (x + 2) (x + 4) (x + 6) + 16 = y^{2}

，且

100 \leq y \leq 200

，求正整数

x

的值．

查看试题解析

23. 阅读理解：对于任意一个四位数，若千位数字与十位数字均为奇数，百位数字与个位数字均为偶数，则称这个四位数为“均衡数”.将一个“均衡数”的千位数字与十位数字组成一个新的两位数m，原来千位数字作为m的十位数字；将一个“均衡数”的百位数字与个位数字组成另一个新的两位数n，原来百位数字作为n的十位数字.例如：“均衡数”3812，则

m = 31 ， n = 82

.若

m ， n

各个数位上的数字都不为零且十位数字大于个位数字，则将m中的任意一个数字作为一个新的两位数的十位数字，n中的任意一个数字作为这个新的两位数的个位数字，按这个方式产生的所有新的两位数的和记为

F (m ， n)

.例如：

m = 31 ， n = 82

时，

F (31 ， 82) = 38 + 32 + 18 + 12 = 100

.

(1)、3456（填“是”或“不是”）“均衡数”，最小的“均衡数”为；

(2)、若

F (m ， n)

是一个完全平方数，请求出所有满足条件的“均衡数”.

查看试题解析

24. 观察以下等式：

第一个等式： $3^{2} - 1 = 9 - 1 = 2 \times (1 + 3)$

第二个等式： $3^{3} - 1 = 27 - 1 = 2 \times (1 + 3 + 9)$

第三个等式： $3^{4} - 1 = 81 - 1 = 2 \times (1 + 3 + 9 + 27)$

…

按照上述规律，解决下列问题：

(1)、写出第四个等式．

(2)、写出你猜想的第

n

个等式： ▲ （用含

n

的等式表示），并证明．

查看试题解析

25. 观察以下等式：

第1个等式： $\frac{1}{2} + \frac{1}{1 \times 2}$ =1，

第2个等式： $\frac{1}{3} + \frac{1}{2 \times 3} = \frac{1}{2}$ ，

第3个等式： $\frac{1}{4} + \frac{1}{3 \times 4} = \frac{1}{3}$ ，

第4个等式： $\frac{1}{5} + \frac{1}{4 \times 5} = \frac{1}{4}$ ，

第5个等式： $\frac{1}{6} + \frac{1}{5 \times 6} = \frac{1}{5}$ ，

……

按照以上规律，解决下列问题：

(1)、写出第6个等式：．

(2)、写出你猜想的第n个等式： ▲ (用含n的式子表示)，并证明其正确性．

查看试题解析

26.

(1)、计算：

{(3 - π)}^{0} - | \sqrt{12} - 2 | + {(\frac{1}{3})}^{- 2} + 4 s i n 60 ° - {(- 1)}^{2022}

；

(2)、先化简．再求值：

(1 - \frac{3}{x + 2}) \div \frac{x^{2} - 1}{x + 2}

，并从-2，-1，0，1中选一个合适的数作为x的值代入求值．

查看试题解析

27. 计算

(1)、化简：

\frac{x - 3}{x^{2} - 6 x + 9} + \frac{x^{2} + 3 x}{x + 3} \div x

(2)、解不等式组

{\begin{array}{l} 3 x - 9 < 9 - 3 x \\ 4 x + 2 > \frac{3 + x}{4} \end{array}

，并写出它的整数解．

查看试题解析

28. 不等式组

{\begin{array}{l} 2 (1 - x) < x + 8 \\ \frac{3 x - 2}{6} < \frac{x - 1}{3} \end{array}

(1)、解此不等式组；

(2)、若m是此不等式组的最大整数解，求

1 + m + m^{2} + \cdot \cdot \cdot + m^{2021} + m^{2022}

的值．

查看试题解析

29. 观察以下等式：

第1个等式：2²﹣1²＝2×1+1，

第2个等式：3²﹣2²＝2×2+1，

第3个等式：4²﹣3²＝2×3+1，

第4个等式：5²﹣4²＝2×4+1，

…

按照以上规律，解决下列问题：

(1)、写出第5个等式：．

(2)、写出你猜想的第n个等式： ▲ （用含n的等式表示），并证明．

查看试题解析

30. 已知：如图，数轴上点A所表示的数为4，点A关于原点的对称点为点B，设点B所表示的数为x．

(1)、直接写出：

x =

；

(2)、求

(\frac{1}{x - 1} - \frac{1}{x + 1}) \div \frac{x}{2 x^{2} - 2}

的值．

查看试题解析

备考浙教版中考数学题型专项训练 数与式解答题专练

一、综合题

备考浙教版中考数学题型专项训练数与式解答题专练