云南省曲靖市罗平县2022年九年级初中学业水平考试第二次模拟测试数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
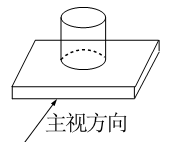
1. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
 A、
A、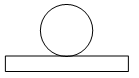 B、
B、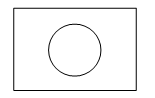 C、
C、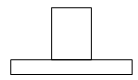 D、
D、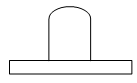 2. 下列计算中正确的是()A、 B、2-3=-6 C、 D、3. 如图,直线 , ,则 的度数是( )
2. 下列计算中正确的是()A、 B、2-3=-6 C、 D、3. 如图,直线 , ,则 的度数是( ) A、 B、 C、 D、4. 已知一个多边形内角和是外角和的4倍,则这个多边形是( )A、八边形 B、九边形 C、十边形 D、十二边形5. 15名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前8名,则他不仅要知道自己的成绩,还应知道这15名学生成绩的( )A、平均数 B、众数 C、方差 D、中位数6. 函数 的自变量x的取值范围是()A、 B、 C、 且 D、 且7. 若 ,则 的值为( )A、 B、4 C、4或 D、20或8. 已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖中这家商店( )A、不盈不亏 B、盈利20元 C、盈利10元 D、亏损20元9. 如图,已知△ABC .
A、 B、 C、 D、4. 已知一个多边形内角和是外角和的4倍,则这个多边形是( )A、八边形 B、九边形 C、十边形 D、十二边形5. 15名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前8名,则他不仅要知道自己的成绩,还应知道这15名学生成绩的( )A、平均数 B、众数 C、方差 D、中位数6. 函数 的自变量x的取值范围是()A、 B、 C、 且 D、 且7. 若 ,则 的值为( )A、 B、4 C、4或 D、20或8. 已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖中这家商店( )A、不盈不亏 B、盈利20元 C、盈利10元 D、亏损20元9. 如图,已知△ABC .⑴以点A为圆心,以适当长为半径画弧,交AC于点M , 交AB于点N .
⑵分别以M , N为圆心,以大于 MN的长为半径画弧,两弧在∠BAC的内部相交于点P .
⑶作射线AP交BC于点D .
⑷分别以A , D为圆心,以大于 AD的长为半径画弧,两弧相交于G , H两点.
⑸作直线GH , 交AC , AB分别于点E , F .
依据以上作图,若AF=2,CE=3,BD= ,则CD的长是( )
 A、 B、1 C、 D、410. 如图,在 中, , 和 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 ,垂足为C , 与AD相交于点E . 若 , ,则 的值为( )
A、 B、1 C、 D、410. 如图,在 中, , 和 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 ,垂足为C , 与AD相交于点E . 若 , ,则 的值为( ) A、 B、 C、 D、11. 已知关于x的分式方程 的解为非负数,则m的取值范围是( )A、 B、 且 C、 D、 且12. 如图,正六边形 的边长为2,以 为圆心, 的长为半径画弧,得 ,连接 , ,则图中阴影部分的面积为( )
A、 B、 C、 D、11. 已知关于x的分式方程 的解为非负数,则m的取值范围是( )A、 B、 且 C、 D、 且12. 如图,正六边形 的边长为2,以 为圆心, 的长为半径画弧,得 ,连接 , ,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若 与 的和为0,则 .14. 在平面直角坐标系中,若点 与点 关于原点对称,则经过 的反比例函数解析式是 .15. 已知 , 是方程 的两根,则 的值为 .16. 如图,在平面直角坐标系中,等腰直角三角形的直角边在轴上,点在第一象限,且 , 以点为直角顶点,为一直角边作等腰直角三角形 , 再以点为直角顶点,为直角边作等腰直角三角形依此规律,则点的坐标是.
 17. 如图,在平面直角坐标系 中,直线 与 相交于A,B两点,且点A在x轴上,则弦 的长为.
17. 如图,在平面直角坐标系 中,直线 与 相交于A,B两点,且点A在x轴上,则弦 的长为. 18. 阅读理解:对于 这类特殊的代数式可以按下面的方法分解因式: 理解运用:如果 ,那么 ,即有 或 ,因此,方程 和 的所有解就是方程 =0 的解.解决问题:求方程 的解为 .
18. 阅读理解:对于 这类特殊的代数式可以按下面的方法分解因式: 理解运用:如果 ,那么 ,即有 或 ,因此,方程 和 的所有解就是方程 =0 的解.解决问题:求方程 的解为 .三、解答题
-
19. 先化简 ,再从 中选择适当的数代入求值.20. 我市华恒小区居民在“一针疫苗一份心,预防接种尽责任”的号召下,积极联系社区医院进行新冠疫苗接种.为了解接种进度,该小区管理人员对小区居民进行了抽样调查,按接种情况可分如下四类:A类——接种了只需要注射一针的疫苗:B类——接种了需要注射二针,且二针之间要间隔一定时间的疫苗;C类——接种了要注射三针,且每二针之间要间隔一定时间的疫苗;D类——还没有接种,图1与图2是根据此次调查得到的统计图(不完整).

请根据统计图回答下列问题.
(1)、此次抽样调查的人数是多少人?(2)、接种B类疫苗的人数的百分比是多少?接种C类疫苗的人数是多少人?(3)、请估计该小区所居住的18000名居民中有多少人进行了新冠疫苗接种.(4)、为了继续宣传新冠疫苗接种的重要性,小区管理部门准备在已经接种疫苗的居民中征集2名志愿宣传者,现有3男2女共5名居民报名,要从这5人中随机挑选2人,求恰好抽到一男和一女的概率是多少.21. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 . (1)、求证:四边形 是菱形;(2)、若 ,求 的面积.22. 某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
(1)、求证:四边形 是菱形;(2)、若 ,求 的面积.22. 某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:出厂价
成本价
排污处理费
甲种塑料
2100(元/吨)
800(元/吨)
200(元/吨)
乙种塑料
2400(元/吨)
1100(元/吨)
100(元/吨)
另每月还需支付设备管理、维护费20000元
(1)、设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);(2)、已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?

