天津市红桥区2022年九年级第一次模拟数学试题

试卷更新日期：2022-05-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $(- 2) \times 6$ 的结果等于（）

A、 $- 12$ B、 $12$ C、 $- 4$ D、 $4$

查看试题解析
2. 2sin60°的值等于（）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
3. 下列图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 据2022年3月30日《天津日报》报道，我市首个百万千瓦光伏发电“盐光互补”项目进入建设阶段．该项目投产后，预计年可节约发电标煤的501200吨．将501200用科学记数法表示应为（）

A、 $0.5012 \times 10^{6}$ B、 $5.012 \times 10^{5}$ C、 $50.12 \times 10^{4}$ D、 $501.2 \times 10^{3}$

查看试题解析
5. 如图是一个由6个相同的正方体组成的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{22}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
7. 方程组 ${\begin{matrix} 3 x + 2 y = 5 ， \\ 2 x + y = 3 \end{matrix}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 ， \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 1 ， \\ y = 1 \end{array}$ C、 ${\begin{matrix} x = 0 ， \\ y = 3 \end{matrix}$ D、 ${\begin{array}{l} x = - 1 ， \\ y = - 1 \end{array}$

查看试题解析
8. 若点 $A (- 5 ， y_{1}) ， B (- 2 ， y_{2}) ， C (1 ， y_{3})$ 都在反比例函数 $y = \frac{10}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
9. 计算 $\frac{1}{x - 1} - \frac{1}{x + 1}$ 的结果是（）

A、 $- 2$ B、 $\frac{2}{x - 1}$ C、 $\frac{2}{x + 1}$ D、 $\frac{2}{x^{2} - 1}$

查看试题解析
10. 如图，在平面直角坐标系中，A ， B两点的坐标分别是 $(8 ， 0)$ ， $(0 ， 6)$ ，点C为线段 $A B$ 的中点，则 $O C$ 的长等于（）

A、 $\sqrt{5}$ B、 $\frac{5}{2}$ C、5 D、10

查看试题解析
11. 如图，将 $△ A B C$ 绕点B顺时针旋转得到 $△ D B E$ ，点C的对应点为E ，点A的对应点D落在 $A C$ 的延长线上，连接 $E C$ ．则下列结论一定正确的是（）

A、 $∠ B A C = ∠ D B E$ B、 $A B = C E$ C、 $∠ B D E = ∠ B D C$ D、 $B C = E D$

查看试题解析
12. 下表中列出的是二次函数 $y = a x^{2} + b x + c$ （a ， b ， c为常数， $a \neq 0$ ）的自变量x与函数y的几组对应值．

x

…

$- 2$

0

1

3

…

y

…

6

$- 4$

$- 6$

$- 4$

…

有下列结论：① $c = - 4 a$ ；②当 $- 2 \leq x \leq 3$ 时，y的取值范围是 $- 6 \leq y \leq 6$ ；③ $9 a + 2 b + c < 0$ ；④关于x的方程 $a x^{2} + b x = m^{2} - 2$ 有两个不相等的实数根．其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

13. 计算 ${(2 x)}^{3} + x^{2}$ 的结果等于．

查看试题解析
14. 计算 $(\sqrt{3} + \sqrt{6}) (\sqrt{3} - \sqrt{6})$ 的结果等于．

查看试题解析
15. 不透明袋子中装有10个球，其中有3个红球、3个绿球和4个蓝球，这些球除颜色外无其他差别，从袋子中随机取出1个球，则它是红球的概率是．

查看试题解析
16. 将直线 $y = x + 1$ 向右平移2个单位长度后，所得直线的解析式是．

查看试题解析
17. 如图，以 $R t △ A B C$ 的斜边 $A B$ 为一边，在 $△ A B C$ 的同侧作正方形 $A B D E$ ，设正方形的中心为O ，连接 $O C$ ．若 $A B = 13$ ， $A C = 5$ ，则 $O C$ 的长为．

查看试题解析

三、解答题

18. 如图，在每个小正方形的边长为1的网格中，点A ， B ， C均在格点上，以 $A B$ 为直径的半圆的圆心为O ．

(1)、 $A B$ 的长等于；

(2)、设P是半圆上的动点，Q是线段 $P C$ 的中点．当 $△ Q O C$ 的面积最大时，请在如图所示的网格中，用无刻度的直尺，画出点Q ，并简要说明点Q的位置是如何找到的（不要求证明）．

查看试题解析
19. 解不等式组 ${\begin{array}{l} x + 1 \geq - 1 ， ① \\ 2 x - 3 \leq 1. ② \end{array}$
请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
20. 某学校为了解学生某一周参加家务劳动的情况，从各年级共1500名学生中随机抽取了部分学生，对其参加家务劳动的次数进行了统计，会制出如下的统计图①和图②．根据相关信息，解答下列问题：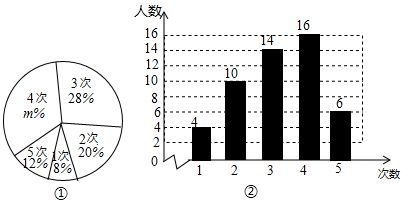

(1)、本次接受随机抽样调查的学生人数为，图①中m的值为；

(2)、求统计的这组参加家务劳动次数数据的众数、中位数和平均数；

(3)、根据统计的这组参加家务劳动次数数据，估计该校学生中这周参加家务劳动次数大于3的学生人数．

查看试题解析
21. 在 $△ A B C$ 中， $∠ C = 90 °$ ．以边 $A B$ 上一点O为圆心， $O A$ 为半径的圆与 $B C$ 相切于点D ，分别交 $A B ， A C$ 于点E ， F ．

(1)、如图①，连按 $A D$ ，若 $∠ C A D = 25 °$ ，求 $∠ B$ 的大小；

(2)、如图②，若点F为 $\overset{⌢}{A D}$ 的中点，求 $∠ B$ 的大小．

查看试题解析
22. 如图，热气球的探测器显示，从热气球所在位置A处看一栋楼顶部B处的仰角为 $35 °$ ，看这栋楼底部C处的俯角为 $61 °$ ．已知这栋楼 $B C$ 的高度为 $300m$ ，求热气球所在位置与楼的水平距离（结果保整数）

参考数据： $\tan 35 ° \approx 0.70 ， \tan 61 ° \approx 1.80$

查看试题解析

23. 在“看图说故事”活动中，栽学习小组结合图象设计了一个问题情境．

已知小明家、小刚家、体育馆、图书馆依次在同一条直线上．小明从家出发，匀速骑行 $0 .5h$ 到达体育馆；在体有馆停留一段时间后，匀速步行 $0 .2h$ 到达小刚家；在小刚家停留 $0 .5h$ 后，两人一起匀速骑行 $0 .3h$ 后到达图书馆；在图书馆停留 $0 .5h$ 后，两人一起匀速骑行返回各自的家中．给出的图象反映了这个过程中小明离开家的距离 $y km$ 与离开家的时间 $x h$ 之间的对应关系．

请根据相关信息，解答下列问题：

(1)、填表：

小明离开家的时间/h	0.1	0.4	0.5	2.5	3.3
小明离开家的距离/ $km$	1.2			5

(2)、填空：

①小明家与小刚家之间的距离为 $km$ ；

②小明从体育馆到小刚家的步行速度为 $km/h$ ；

③两人从小刚家到图书馆的骑行速度为 $km/h$ ；

④当小明离开家的距高为 $4km$ 时，他离开家的时间为h ．

(3)、当

2.7 \leq x \leq 4

时，请直接写出y关于x的函数解析式．

查看试题解析

24. 在平面直角坐标系中，O为原点，点 $A (- 2 ， 0) ， B (6 ， 0)$ ，点C在y轴的正半轴上， $∠ A C B = 90 °$ ．

(1)、如图①，求点C的坐标；

(2)、将 $△ A O C$ 沿x轴向右平移得 $△ A^{'} O^{'} C^{'}$ ，点A ， O ， C的对应点分别为 $A^{'} ， O^{'} ， C^{'}$ ．设 $O O^{'} = t ， △ A^{'} O^{'} C^{'}$ 与 $△ O B C$ 重叠部分的面积为S ．
①如图②，当 $△ A^{'} O^{'} C^{'}$ 与 $△ O B C$ 重叠部分为四边形时， $A^{'} C^{'} ， O^{'} C^{'}$ 分别与 $B C$ 相交于点D ， E ，试用含有t的式子表示S ，并直接写出t的取值范围；

②当S取得最大值时，求t的值（直按写出结果即可）．

查看试题解析
25. 已知抛物线 $y = a x^{2} + b x - 4$ （a ， b为常数， $a \neq 0$ ）交x轴于 $A (- 1 ， 0)$ ， $B (4 ， 0)$ 两点，交y轴于点C ．

(1)、求该抛物线的解析式；

(2)、点P为第四象限内该抛物线上一点，连接 $P B$ ，过点C作CQ//BP交x轴于点Q ，连接 $P Q$ ，求 $△ P B Q$ 面积的最大值及此时点P的坐标；

(3)、在（2）的条件下，将抛物线 $y = a x^{2} + b x - 4$ 向右平移经过点 $(\frac{1}{2} ， 0)$ 时，得到抛物线 $y = a_{1} x^{2} + b_{1} x + c_{1}$ ．设E是抛物线 $y = a_{1} x^{2} + b_{1} x + c_{1}$ 对称轴上的点，在坐标平面内是否存在点F ，使得以A ， P ， E ， F为顶点的四边形为矩形，若存在，请求出点F的坐标，若不存在，请说明理由．

查看试题解析

x	…	$- 2$	0	1	3	…
y	…	6	$- 4$	$- 6$	$- 4$	…