天津市河北区2022年九年级中考一模数学试卷
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 计算 的结果是()A、5 B、6 C、-5 D、-62. 的值为( )A、1 B、-1 C、 D、3. 2022年冬奥会颁奖花束采用了“海派绒线编结技艺”这一上海非遗手工艺技术,共用花束1251束,累计花材16731支,仅一朵玫瑰,就需要一位编结师耗费至少5小时,所有花束的全部手工制作时间近5万小时,将16731用科学记数法表示应为()A、 B、 C、 D、4. 下列交通标志中,是中心对称图形的是()A、
 B、
B、 C、
C、 D、
D、 5. 一个由5个相同的正方体组成的立体图形,如图所示,则这个立体图形的左视图是( )
5. 一个由5个相同的正方体组成的立体图形,如图所示,则这个立体图形的左视图是( )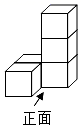 A、
A、 B、
B、 C、
C、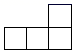 D、
D、 6. 估计 的值在( )A、5和6之间 B、4和5之间 C、3和4之间 D、2和3之间7. 方程组 的解是( )A、 B、 C、 D、8. 如图,四边形AOCD是菱形,O , C两点的坐标分别是(0,0),(2, 0), ,则点D的坐标为( )
6. 估计 的值在( )A、5和6之间 B、4和5之间 C、3和4之间 D、2和3之间7. 方程组 的解是( )A、 B、 C、 D、8. 如图,四边形AOCD是菱形,O , C两点的坐标分别是(0,0),(2, 0), ,则点D的坐标为( ) A、(3, ) B、( ,2) C、(3,1) D、(4,3)9. 计算 的结果是( )A、 B、 C、2 D、-210. 已知点(-2, ),(-1, ),(1, )都在反比例函数 的图象上,那么 , , 的大小关系是( )A、 B、 C、 D、11. 如图,在△ABC中, , ,将△ABC绕点C按逆时针方向旋转 后得到△DEC , 设CD交AB于点F , 连接AD , 若 ,则旋转角 的度数为( )
A、(3, ) B、( ,2) C、(3,1) D、(4,3)9. 计算 的结果是( )A、 B、 C、2 D、-210. 已知点(-2, ),(-1, ),(1, )都在反比例函数 的图象上,那么 , , 的大小关系是( )A、 B、 C、 D、11. 如图,在△ABC中, , ,将△ABC绕点C按逆时针方向旋转 后得到△DEC , 设CD交AB于点F , 连接AD , 若 ,则旋转角 的度数为( ) A、 B、 C、 D、12. 已知抛物线 (a , b , c是常数,且 )的图象的对称轴为直线 ,与x轴的一个交点为(-4,0),与y轴的交点在(0,0)和(0,3)(不包括这两点)之间,有下列结论:① ;②函数可取得最大值 ;③ .其中,正确结论的个数是( )A、3 B、2 C、1 D、0
A、 B、 C、 D、12. 已知抛物线 (a , b , c是常数,且 )的图象的对称轴为直线 ,与x轴的一个交点为(-4,0),与y轴的交点在(0,0)和(0,3)(不包括这两点)之间,有下列结论:① ;②函数可取得最大值 ;③ .其中,正确结论的个数是( )A、3 B、2 C、1 D、0二、填空题
-
13. 计算: .14. 计算: .15. 小明把一副扑克牌中带数字8的扑克牌全部拿出给小华抽,则小华抽到黑桃8的概率为 .16. 已知一次函数 的图象经过第一、二、三象限,则a的取值范围是 .17. 如图,点E为正方形ABCD的边CD的中点,连接AE , BE , BE交对角线AC于点F , 连接FD交AE于点G , 如果DF=4,那么AB的长为 .

三、解答题
-
18. 如图,在每个边长为1的小正方形网格中,点A , B均在格点上,以AB为直径作圆,点M为 的中点.
 (1)、线段AB的长度等于;(2)、请用无刻度的直尺,在圆上找一点P , 使得 ,并简要说明点P的位置是如何找到的(不要求证明)19. 解不等式组
(1)、线段AB的长度等于;(2)、请用无刻度的直尺,在圆上找一点P , 使得 ,并简要说明点P的位置是如何找到的(不要求证明)19. 解不等式组请结合解题过程,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .20. 某校初中年级举行防疫知识竞赛,随机抽取了一个班的竞赛成绩(单位:分),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题.
(4)、原不等式组的解集为 .20. 某校初中年级举行防疫知识竞赛,随机抽取了一个班的竞赛成绩(单位:分),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题. (1)、本次接受调查的学生人数为 , 图①中m的值为;(2)、求统计的这个班竞赛成绩数据的平均数、众数和中位数.21. 已知AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线DC交BA的延长线于点D , 连接BC .
(1)、本次接受调查的学生人数为 , 图①中m的值为;(2)、求统计的这个班竞赛成绩数据的平均数、众数和中位数.21. 已知AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线DC交BA的延长线于点D , 连接BC . (1)、如图①,连接AC , 若 ,求∠ACD的大小;(2)、如图②,E为 上一点,连接OE , CE , 若四边形ODCE为平行四边形,求∠B的大小.22. 如图,小明、小华分别位于一条笔直公路PQ上的两点A , B处,点C处为一超市.测得 , ,A , B之间距离为3.8km,求小明、小华分别距离超市多少千米(结果保留小数点后一位).
(1)、如图①,连接AC , 若 ,求∠ACD的大小;(2)、如图②,E为 上一点,连接OE , CE , 若四边形ODCE为平行四边形,求∠B的大小.22. 如图,小明、小华分别位于一条笔直公路PQ上的两点A , B处,点C处为一超市.测得 , ,A , B之间距离为3.8km,求小明、小华分别距离超市多少千米(结果保留小数点后一位).参考数据: , , , , , .
 23. 某校计划从甲、乙两家体育用品店中选择一家购买一批乒乓球拍以丰富学生的校园生活.已知甲、乙两家体育用品店的每副乒乓球拍标价均为30元,现两家分别推出以下优惠方案:甲体育用品店:购买10副以上,从第11副开始按标价的七折出售;乙体育用品店:从第1副起就按标价的八五折出售.
23. 某校计划从甲、乙两家体育用品店中选择一家购买一批乒乓球拍以丰富学生的校园生活.已知甲、乙两家体育用品店的每副乒乓球拍标价均为30元,现两家分别推出以下优惠方案:甲体育用品店:购买10副以上,从第11副开始按标价的七折出售;乙体育用品店:从第1副起就按标价的八五折出售.设该校计划购买乒乓球拍的副数为x(x为正整数)
(1)、根据题意,填写下表:购买副数
5
10
15
30
…
在甲体育用品店购买的费用(元)
150
405
…
在乙体育用品店购买的费用(元)
127.5
382.5
…
(2)、若该校计划用1581元购买乒乓球拍,则该校选择在哪一家体育用品店购买的兵乓球拍比较多?(3)、当 时,该校在哪家体育用品店购买更合算?并说明理由.24. 将一个含 角的直角三角形纸片AOB放置在平面直角坐标系中, ,点B(0,2),D是边AB上一点(不与点A , B重合),沿OD折叠该纸片,得点B的对应点C .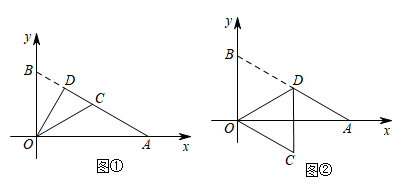 (1)、如图①,当点C落在AB边上时,求AC的长;(2)、如图②,当 轴时,求点C的坐标;(3)、当DC所在直线与x轴的夹角为 时,求点D的坐标(直接写出结果即可).25. 已知抛物线 (b , c为常数)与x轴交于A(3,0),C两点,与y轴相交于点B , 点M为线段AB上一点.(1)、当 时,求该抛物线的顶点坐标;(2)、若点N(-b-2, )是抛物线在第三象限内的点,有一点P(-5,0),当 时,求b的值;(3)、在(1)的条件下, ,点E是y轴上一点,在抛物线上是否存在点F , 使得以A , M , E , F为顶点的四边形为平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
(1)、如图①,当点C落在AB边上时,求AC的长;(2)、如图②,当 轴时,求点C的坐标;(3)、当DC所在直线与x轴的夹角为 时,求点D的坐标(直接写出结果即可).25. 已知抛物线 (b , c为常数)与x轴交于A(3,0),C两点,与y轴相交于点B , 点M为线段AB上一点.(1)、当 时,求该抛物线的顶点坐标;(2)、若点N(-b-2, )是抛物线在第三象限内的点,有一点P(-5,0),当 时,求b的值;(3)、在(1)的条件下, ,点E是y轴上一点,在抛物线上是否存在点F , 使得以A , M , E , F为顶点的四边形为平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.