备考浙教版中考数学题型专项训练 数与式填空题专练
试卷更新日期:2022-05-23 类型:三轮冲刺
一、填空题
-
1. 如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有种.
 2. 如图所示,将形状、大小完全相同的“
2. 如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“ ”的个数为a1 , 第2幅图形中“
”的个数为a1 , 第2幅图形中“ ”的个数为a2 , 第3幅图形中“
”的个数为a2 , 第3幅图形中“ ”的个数为a3 , …,以此类推,则的值为 .
”的个数为a3 , …,以此类推,则的值为 . 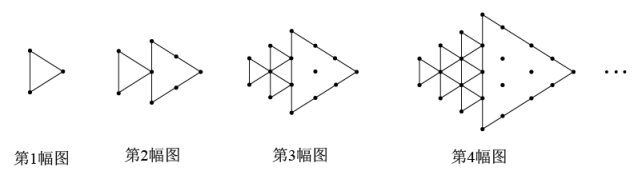 3. 【问题提出】计算(其中是正整数)
3. 【问题提出】计算(其中是正整数)【问题探究】为解决上面的数学问题,我们可以运用数形结合的思想方法,借助图1所示的三角形,把数量关系和几何图形巧妙地结合起来进行探究.图1中,

第1行圆圈中的数为1,即;
第2行两个圆圈中数的和为2+2=2×2,
即;
第3行三个圆圈中数的和为3+3+3=3×3
即;
……;
第行个圆圈中数的和为 , 即.所有圆圈中数的和为.
要解决上面的问题,我们不妨先从特例入手:
探究一:计算.
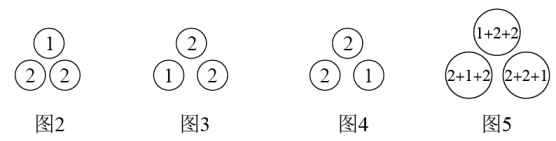
将图2按逆时针方向两次旋转得到图3、图4.观察这三个图形,可以发现同一位置圆圈的数字之和都是5(如图5),而图5共有(1+2)个这样的圆圈,因此图5中所有数字之和为5×(1+2).则图2中所有数字之和为 , 所以得到等式.
(1)、探究二:计算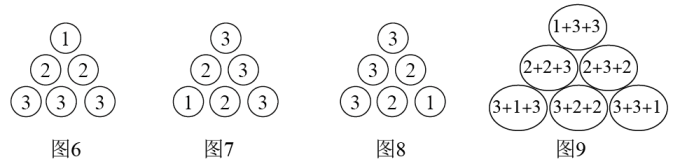
仿照上述方法,将图6按逆时针方向两次旋转得到图7、图8.观察这三个图形,可以发现同一位置圆圈的数字之和都是(如图9),而图9共有个这样的圆圈,因此图9中所有数字之和为.那么图6中所有数字之和为 , 所以得到等式.(仿照上述方法,写出探究得出的式子).
(2)、探究三:计算.(仿照上述方法,直接写出结果).(3)、【问题解决】.(仿照上述方法,直接写出探究得出的式子,用含的代数式表示)(4)、【拓广应用】计算:.(直接写出结果)
4. 若素数p,使得 是一个完全平方数,则p=.(若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数.)5. 观察下列表格中的每组数,根据规律得出 的值为.第一组数
6
8
10
第二组数
8
15
17
第三组数
10
24
26
第四组数
12
35
37
…
…
…
…
…
24
a
b
6. 小明同学利用计算机设计了一个程序, 输入和输出的情况如下表。他发现从第三个输出项起的每一项都与这一项的前面两个输出项有关。按此规律, 从1开始一直输入到 2022后, 输出项的系数与次数均为奇数的项共有个.输入
1
2
3
4
5
6
7
8
输出
7. 观察下面三行数:1,﹣4,9,﹣16,25,﹣36,…;
﹣1,﹣6,7,﹣18,23,﹣38,…;
﹣2,8,﹣18,32,﹣50,72,…;
那么取每行数的第10个数,则这三个数的和为 .
8. 已知 ,则 .9. 定义 ,比如, , .若实数 满足 ,并且这个关于 的方程有两个不相等的实数解,则 的取值范围是 .10. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性,从图中取一列数:1,3,6,10,…,分别记为 , , , ,…,那么 的值是.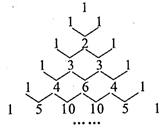 11. 随着我国疫情的有效控制,各地打造了众多春游景点供市民休闲娱乐.某区特别打造了多彩植物园、亲子游乐园、劳动体验园吸引游客.3月份多彩植物园、亲子游乐园、劳动体验园接待游客数量之比为 .为增加游客数量,该地区通过发抖音、转发朋友圈等多种方式加大宣传力度,预计4月份三个园区接待的游客总人数在3月份的基础上会增加.但因为多彩植物园中部分花期已过,多彩植物园的游客人数在3月份的基础上将减少 .这样4月份,多彩植物园接待的游客总人数占三个园区接待游客总人数的 ,而亲子游乐园、劳动体验园4月份接待游客人数之比将达到 ,则亲子游乐园新增的人数与4月份这三个园区的总人数之比是12. 如图,已知直线 : ,过点 作x轴的垂线交直线 于点 ,在线段 右侧作等边三角形 ,过点 作x轴的垂线交x轴于 ,交直线L于点 ,在线段 右侧作等边三角形 ,按此作法继续下去则 的纵坐标为 . (n为正整数)
11. 随着我国疫情的有效控制,各地打造了众多春游景点供市民休闲娱乐.某区特别打造了多彩植物园、亲子游乐园、劳动体验园吸引游客.3月份多彩植物园、亲子游乐园、劳动体验园接待游客数量之比为 .为增加游客数量,该地区通过发抖音、转发朋友圈等多种方式加大宣传力度,预计4月份三个园区接待的游客总人数在3月份的基础上会增加.但因为多彩植物园中部分花期已过,多彩植物园的游客人数在3月份的基础上将减少 .这样4月份,多彩植物园接待的游客总人数占三个园区接待游客总人数的 ,而亲子游乐园、劳动体验园4月份接待游客人数之比将达到 ,则亲子游乐园新增的人数与4月份这三个园区的总人数之比是12. 如图,已知直线 : ,过点 作x轴的垂线交直线 于点 ,在线段 右侧作等边三角形 ,过点 作x轴的垂线交x轴于 ,交直线L于点 ,在线段 右侧作等边三角形 ,按此作法继续下去则 的纵坐标为 . (n为正整数)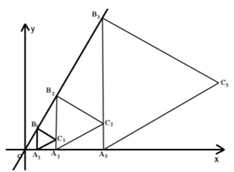 13. 观察下列等式: , , ,….按照此规律,则第 个式子是 .14. 规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;③一组对边平行,一条对角线平分一个内角的四边形是广义菱形;④若M、N的坐标分别为(0,2),(0, 2),P是二次函数 图象上在第一象限内的任意一点,PQ垂直直线 于点Q , 则四边形PMNQ是广义菱形.其中正确的是 . (填序号)15. 如果一个两位数a的个位数字与十位数字都不是零,且互不相同,我们称这个两位数为“跟斗数”,定义新运算:将一个“跟斗数”的个位数字与十位数字对调,把这个新两位数与原两位数的和与11的商记 ,例如:a=13,对调个位数字与十位数字得到新两位数31,新两位数与原两位数的和,31+13=44,和与11的商44÷11=4,所以 .根据以上定义,回答下列问题:(1)、计算: .(2)、若一个“跟斗数”b的十位数字是k , 个位数字是2(k+1),且 ,则“跟斗数”b= .(3)、若m , n都是“跟斗数”,且m+n=100,则 .16. 一列数按规律排列如下: , , , , , , ,…, 若第n个数为 , 则n = 。17. 如图所示,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5……过A1、A2、A3、A4、A5……分别作x轴的垂线与反比例函数y= 的图象交于点P1、P2、P3、P4、P5……并设△OA1P1、△A1A2P2、△A2A3P3……面积分别为S1、S2、S3……,按此作法进行下去,则S2020的值为。
13. 观察下列等式: , , ,….按照此规律,则第 个式子是 .14. 规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;③一组对边平行,一条对角线平分一个内角的四边形是广义菱形;④若M、N的坐标分别为(0,2),(0, 2),P是二次函数 图象上在第一象限内的任意一点,PQ垂直直线 于点Q , 则四边形PMNQ是广义菱形.其中正确的是 . (填序号)15. 如果一个两位数a的个位数字与十位数字都不是零,且互不相同,我们称这个两位数为“跟斗数”,定义新运算:将一个“跟斗数”的个位数字与十位数字对调,把这个新两位数与原两位数的和与11的商记 ,例如:a=13,对调个位数字与十位数字得到新两位数31,新两位数与原两位数的和,31+13=44,和与11的商44÷11=4,所以 .根据以上定义,回答下列问题:(1)、计算: .(2)、若一个“跟斗数”b的十位数字是k , 个位数字是2(k+1),且 ,则“跟斗数”b= .(3)、若m , n都是“跟斗数”,且m+n=100,则 .16. 一列数按规律排列如下: , , , , , , ,…, 若第n个数为 , 则n = 。17. 如图所示,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5……过A1、A2、A3、A4、A5……分别作x轴的垂线与反比例函数y= 的图象交于点P1、P2、P3、P4、P5……并设△OA1P1、△A1A2P2、△A2A3P3……面积分别为S1、S2、S3……,按此作法进行下去,则S2020的值为。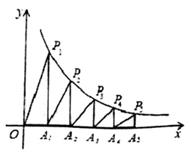 18. 分解因式:.19. 对于实数x,规定表示不小于x的最小整数,例如 , , ;若 , 则x的取值范围是 .20. 已知 , 则代数式的值等于 .21. 化简 .22. 观察下列各式: , , , , , , , 根据其中的规律可得 .23. 若非零实a,b满足a2=ab , 即可得的值为 .24. 已知实数x,y满足 , 则 .25. 实践操作:现有两个正方形A,B.如图所示进行两种方式摆放:
18. 分解因式:.19. 对于实数x,规定表示不小于x的最小整数,例如 , , ;若 , 则x的取值范围是 .20. 已知 , 则代数式的值等于 .21. 化简 .22. 观察下列各式: , , , , , , , 根据其中的规律可得 .23. 若非零实a,b满足a2=ab , 即可得的值为 .24. 已知实数x,y满足 , 则 .25. 实践操作:现有两个正方形A,B.如图所示进行两种方式摆放:方式1:将B放在A的内部,得甲图;
方式2:将A,B并列放置,构造新正方形得乙图.
问题解决:对于上述操作,若甲图和乙图阴影部分的面积分别为1和12,则正方形A,B的面积之和为 .
