山西省阳泉市平定县2022年九年级中考模拟数学试题

试卷更新日期：2022-05-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算-3+5的结果为（）

A、8 B、 $- 2$ C、2 D、 $- 8$

查看试题解析
2. 以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2021年5月15日，天向一号探测器成功着陆火星，迈出了我国星际探测征程的重要一步．已知火星与地球的近距离约为5500万公里，5500万用科学记数法表示为（）

A、 $5.5 \times 10^{7}$ B、 $0.55 \times 10^{8}$ C、 $55 \times 10^{6}$ D、 $5.5 \times 10^{3}$

查看试题解析
4. 下列运算正确的是（）

A、 ${(a^{5})}^{2} = a^{7}$ B、 $(a + b) (a - b) = a^{2} + b^{2}$ C、 $2 a^{2} \cdot (- 3 a^{3}) = - 6 a^{5}$ D、 $4 a^{2} \div (- 2 a^{2}) = 2 a$

查看试题解析
5. 方程 ${(x - 2)}^{2} = 3 (x - 2)$ 的解是（）

A、 $x = 5$ B、 $x_{1} = 5 ， x_{2} = 2$ C、 $x_{1} = 1 ， x_{2} = 2$ D、 $x = 2$

查看试题解析
6. 对于反比例函数 $y = - \frac{2}{x}$ ，下列说法错误的是 $($ $)$

A、图象分布在第二、四象限 B、当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 C、图象经过点（1，-2） D、若点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 都在图象上，且 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$

查看试题解析
7. 用一条宽度相等的足够长的纸条打一个结（如图①所示），然后轻轻拉紧，压平就可以得到如图②所示的正五边形 $A B C D E$ . 图②中， $∠ B A C$ 的度数为（）

A、 $108 °$ B、 $36 °$ C、 $120 °$ D、 $30 °$

查看试题解析
8. 我们这样来探究二次根式 $\sqrt{a^{2}}$ 的结果：当 $a > 0$ 时，结果是a本身；当 $a = 0$ 时，结果是零；当 $a < 0$ 时，此时结果是a的相反数，这种分析问题的方法所体现的数学思想是（）

A、分类讨论思想 B、数形结合思想 C、公理化思想 D、转化思想

查看试题解析
9. 如图，直线 $l_{1} ∥ l_{2}$ ，点A在直线 $l_{1}$ 上，以点A为圆心，适当长度为半径画弧，分别交直线 $l_{1}$ 、 $l_{2}$ 于B、C两点，连结AC、BC.若 $∠ A B C = 70^{°}$ ，则 $∠ 1$ 的大小为（）

A、 $20^{°}$ B、 $35^{°}$ C、 $40^{°}$ D、 $70^{°}$

查看试题解析
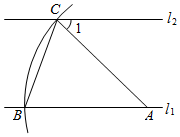10. 如图是一款抛物线型落地灯筒示意图，防滑螺母C为抛物线支架的最高点，灯罩D距离地面1.5米，最高点C距灯柱的水平距离为1.6米，灯柱AB1.5米，若茶几摆放在灯罩的正下方，则茶几到灯柱的距离AE为多少米（）

A、 $3.2$ B、 $0.32$ C、 $2.5$ D、 $1.6$

查看试题解析

二、填空题

11. 分解因式： $x^{3} - 2 x^{2} y + x y^{2} =$ ．

查看试题解析
12. 《增删算法统宗》记载：“有个学生资性好，部孟子三日了，每日增添一倍多，问君每日读多少”？其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍问他每天各读多少个字．已知《孟子》一书共有34685个字，设他第一天读x个字，则列方程为．

查看试题解析
13. 如图，在平面直角坐标系中， $R t Δ A B C$ 的直角顶点 $C$ 的坐标为 $(1 ， 0)$ ，点 $A$ 在 $x$ 轴正半轴上，且 $A C = 2$ .将 $Δ A B C$ 先绕点 $C$ 逆时针旋转 $90^{\circ}$ ，再向左平移3个单位，则变换后点 $A$ 的对应点的坐标为.

查看试题解析
14. 如图，在半径为6的 $⊙ O$ 中，点 $A ， B ， C$ 都在 $⊙ O$ 上，四边形 $O A B C$ 是平行四边形，则图中阴影部分的面积为.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C = 5 ， B C = 8$ ，点D是边 $B C$ 上一点(点D不与点B，C重合)，将 $△ A C D$ 沿 $A D$ 翻折，点C的对应点是E， $A E$ 交 $B C$ 于点F，若 $D E ∥ A B$ ，则 $D F$ 的长为.

查看试题解析

三、解答题

16.

(1)、计算： ${(- \frac{1}{3})}^{- 1} + {(\sqrt{27})}^{0} - 4 \times (- 3) - | - 5 |$

(2)、解方程： $\frac{3 x - 2}{x - 1} = \frac{5}{1 - x}$

查看试题解析
17. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C ， D$ 在 $⊙ O$ 上，且点C是 $\overset{⌢}{B D}$ 的中点，连接 $A C$ ，过点C作 $⊙ O$ 的切线 $E F$ 交射线 $A D$ 于点E. 连接 $B C$ ，已知 $A E = \frac{16}{5}$ ， $A B = 5$ ，试求线段 $B C$ 的长.

查看试题解析
18. 2022年1月初，平定县全面推开创建国家卫生县城活动，县教科局积极开展“小手拉大手，共创卫生城”劳动实践系列活动，全县师生踊跃行动，带动家长和社区群众一起参加，成为县城一道亮丽的风景. 此次活动中，某校为增加学生的环境保护知识，增强学生的环境保护意识，利用课余时间组织九年级一班50名学生参加“环境保护知识小竞赛”，已知每人5道题，班长小王抽查了部分同学的成绩，绘制出如下尚不完整的统计图．

(1)、请补全条形统计图，并求出“答对3道”所对应的圆心角度数；

(2)、被调查学生成绩的中位数是；

(3)、若该校九年级共有1000人，请你估计九年级答对题数超过2道的人数；

(4)、为了增强学生的环境保护意识，班长计划开展环境保护知识交流会，将从所抽取的“答对4道”，“答对5道”的同学中随机抽取两人在会议上发言，请用列表或画树状图法求出所抽到的两人恰好都是“答对4道”的概率．

查看试题解析
19. 《榜样阅读》是中国青年报·中青在线联合酷我音乐共同打造的首档青年阅读分享类音频节目，青春偶像传颂经典、讲述成长故事，用声音掀起新时代青年阅读热潮．某中学为了满足学生的阅读需求，购进了一批图书，并前后两次购买两种书架，其中第一次购买铁质书架 $10$ 个，木质书架 $30$ 个，共花费 $1150$ 元；第二次购买铁质书架 $30$ 个，木质书架 $20$ 个，共花费 $1350$ 元，且两次购买的两种书架单价不变．

(1)、求这两种书架的单价分别为多少元？

(2)、若该学校计划再次购买这两种书架共 $50$ 个，且要求铁质书架的数量不多于木质书架数量的 $3$ 倍，请设计出最省钱的购买方案，并求出最少费用．

查看试题解析
20. 2022年2月20日，举世瞩目的北京冬奥会圆满落下帷幕. 北京冬奥会为绿色办奥、科技办奥贡献了中国样本和中国智慧，让奥运精神点亮更多人的冰雪梦想，并以冰雪运动和奥林匹克精神为纽带，凝聚更团结的力量. 图①，图②分别是一名滑雪运动员在滑雪过程中某一时刻的实物图与示意图，已知运动员的小腿 $E D$ 与斜坡 $A B$ 垂直，大腿 $E F$ 与斜坡 $A B$ 平行， $G$ 为头部，假设 $G ， E ， D$ 三点共线，若大腿弯曲处与滑雪板后端的距离 $E M$ 长为 $0.9 m$ ，该运动员大腿 $E F$ 长为 $0.4 m$ ，且其上半身 $G F$ 长为 $0.8 m$ ， $∠ E M D = 35 °$ ．

(1)、求此刻滑雪运动员的身体与大腿所成的夹角 $∠ G F E$ 的度数；

(2)、求此刻运动员头部G到斜坡 $A B$ 的高度. （结果精确到 $0.1 m$ ，参考数据： $\sin 35 ° \approx 0.57$ ， $\cos 35 ° \approx 0.82$ ， $\tan 35 ° \approx 0.70$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
21. 阅读与思考
请阅读下列材料，并完成相应的任务．

《周髀算经》的启示

早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”. 它被记载于我国古代著名数学著作《周髀算经》中. 如图，已知 $△ A B C$ 是大家熟悉的勾三，股四，弦五的三角形，即 $A C ： B C ： A B = 3 ： 4 ： 5$ ，在其内部作正方形 $D E F G$ 和正方形 $G H M N$ ，点 $D ， N$ 在边 $A B$ 上，点 $E ， F ， H$ 在边 $B C$ 上，点M在边 $A C$ 上，则 $M C = H F$ .

下面是一位同学的部分证明过程：

证明：∵四边形 $D E F G$ 是正方形，

∴ $∠ D E F = ∠ G F E = 90 °$ .

∴ $∠ D E B = ∠ G F H = 90 °$ .

∵四边形 $G H M N$ 是正方形，

∴ $G H = H M ， ∠ G H M = 90 °$ ．

…

任务：

(1)、请按照上面的证明思路，写出该证明的剩余部分；

(2)、若正方形 $D E F G$ 的边长为1，求正方形 $G H M N$ 的边长．

查看试题解析
22. 综合与实践：

(1)、问题情境：如图，点E是正方形 $A B C D$ 边 $C D$ 上的一点，连接 $B D$ 、 $B E$ ，将 $∠ D B E$ 绕点B顺针旋转90°，旋转后角的两边分别与射线 $D A$ 交于点F和点G．

①线段 $B E$ 和 $B F$ 的数量关系是 ▲ ．

②写出线段 $D E$ 、 $D F$ 和 $B D$ 之间的数量关系．并说明理由；

(2)、操作探究：
在菱形 $A B C D$ 中， $∠ A D C = 60 °$ ，点E是菱形 $A B C D$ 边 $C D$ 所在直线上的－点，连接 $B D$ 、 $B E$ ，将 $∠ D B E$ 绕点B顺时针旋转120°，旋转后角的两边分别与射线 $D A$ 交于点F和点G．

①如图，点E在线段 $D C$ 上时，请探究线段 $D E$ 、 $D F$ 和 $B D$ 之间的数量关系，写出结论并给出证明；

②如图，点E在线段 $C D$ 的延长线上时， $B E$ 交射线 $D A$ 于点M，若 $D E = D C = 2 a$ ，直接写出线段 $F M$ 和 $A G$ 的长度．

查看试题解析
23. 综合与探究
如图，抛物线 $y = - \frac{4}{9} x^{2} + b x + c$ 与y轴交于点 $A (0 ， 8)$ ，与x轴交于点 $B (6 ， 0)$ ，C，过点A作 $A D ∥ x$ 轴与抛物线交于另一点D．

(1)、求抛物线的表达式；

(2)、连接 $A B$ ，点P为 $A B$ 上一个动点，由点A以每秒1个单位长度的速度沿 $A B$ 运动（不与点B重合），运动时间为t，过点P作 $P Q ∥ y$ 轴交抛物线于点Q，求 $P Q$ 与t的函数关系式；

(3)、点M是y轴上的一个点，点N是平面直角坐标系内一点，是否存在这样的点 $M ， N$ ，使得以 $B ， D ， M ， N$ 为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析