山东省淄博市周村区2022年中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 下列图形,既是轴对称图形又是中心对称图形的是()A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是()A、 B、 C、 D、3. 实数 , , 在数轴上的对应点的位置如图所示,若 ,则下列结论中正确的是( )
2. 下列运算正确的是()A、 B、 C、 D、3. 实数 , , 在数轴上的对应点的位置如图所示,若 ,则下列结论中正确的是( )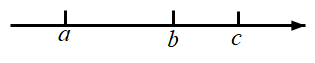 A、 B、 C、 D、4. 如图,AB是 的直径,PA与 相切于点A , 交 于点C . 若 ,则 的度数为( )
A、 B、 C、 D、4. 如图,AB是 的直径,PA与 相切于点A , 交 于点C . 若 ,则 的度数为( ) A、 B、 C、 D、5. 若点M(1-2m , m-1)关于y轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 若点M(1-2m , m-1)关于y轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 一个由完全相同的小正方体组成的几何体的三视图如图所示,若在这个几何体的基础上增加几个相同的小正方体,将其补成一个大正方体,则需要增加的小正方体的个数最少为( )
6. 一个由完全相同的小正方体组成的几何体的三视图如图所示,若在这个几何体的基础上增加几个相同的小正方体,将其补成一个大正方体,则需要增加的小正方体的个数最少为( ) A、6个 B、5个 C、4个 D、3个7. 如图,从一个大正方形中裁去面积为30cm2和48 cm2的两个小正方形,则余下部分的面积为( )
A、6个 B、5个 C、4个 D、3个7. 如图,从一个大正方形中裁去面积为30cm2和48 cm2的两个小正方形,则余下部分的面积为( )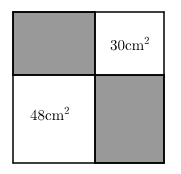 A、78 cm2 B、 cm2 C、 cm2 D、 cm28. 已知关于x的一元二次方程有两个不相等的实数根x1 , x2 . 若 , 则m的值是( )A、2 B、﹣1 C、2或﹣1 D、不存在9. 如图,将半径为15cm的圆形纸片剪去圆心角为144°的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是()
A、78 cm2 B、 cm2 C、 cm2 D、 cm28. 已知关于x的一元二次方程有两个不相等的实数根x1 , x2 . 若 , 则m的值是( )A、2 B、﹣1 C、2或﹣1 D、不存在9. 如图,将半径为15cm的圆形纸片剪去圆心角为144°的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是() A、8cm B、12cm C、20cm D、18cm10. 如图:四边形ABCD为菱形,且对角线BD∥x轴,A、C两点在y轴上,E点在BC上,且BE=2CE,双曲线y=(x>0)经过E、B两点,且 , 则k的值为( )
A、8cm B、12cm C、20cm D、18cm10. 如图:四边形ABCD为菱形,且对角线BD∥x轴,A、C两点在y轴上,E点在BC上,且BE=2CE,双曲线y=(x>0)经过E、B两点,且 , 则k的值为( ) A、3 B、 C、4 D、611. 如图,在平行四边形ABCD中,AD=5cm , CD=3cm , AC⊥CD , 点P从点C出发,以1cm/s的速度沿C→D→A匀速运动,点M从点B出发,以相同的速度沿B→C匀速运动,其中一点停止时,另一点随之停止运动,图2是△PMC的面积S(cm2)随时间t(s)变化的函数图象,若a秒与b秒时△PMC的面积均为 ,则b﹣a的值为( )
A、3 B、 C、4 D、611. 如图,在平行四边形ABCD中,AD=5cm , CD=3cm , AC⊥CD , 点P从点C出发,以1cm/s的速度沿C→D→A匀速运动,点M从点B出发,以相同的速度沿B→C匀速运动,其中一点停止时,另一点随之停止运动,图2是△PMC的面积S(cm2)随时间t(s)变化的函数图象,若a秒与b秒时△PMC的面积均为 ,则b﹣a的值为( )
 A、 B、 C、3 D、12. 如图,点A的坐标是(−2,0),点C是以OA为直径的⊙B上的一动点,点A关于点C的对称点为点P. 当点C在⊙ B上运动时,所有这样的点P组成的图形与直线y=kx-3(k>0)有且只有一个公共点,则k的值是( )
A、 B、 C、3 D、12. 如图,点A的坐标是(−2,0),点C是以OA为直径的⊙B上的一动点,点A关于点C的对称点为点P. 当点C在⊙ B上运动时,所有这样的点P组成的图形与直线y=kx-3(k>0)有且只有一个公共点,则k的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 方程组 的解为14. 如图,在△ABC中,∠C=75°,将△ABC绕点A顺时针旋转到△ADE的位置,点E恰好落在边BC上,且AD∥BC , 则∠D的度数为°.
 15. 一个长方体包装盒的表面展开图如图所示,若此包装盒的容积为1500cm3 , 则该长方体最短的棱的长为cm.
15. 一个长方体包装盒的表面展开图如图所示,若此包装盒的容积为1500cm3 , 则该长方体最短的棱的长为cm. 16. 如图,线段 的端点都在正方形网格的格点上,它们相交于点M.若每个小正方形的边长都是1,则 的值是.
16. 如图,线段 的端点都在正方形网格的格点上,它们相交于点M.若每个小正方形的边长都是1,则 的值是. 17. 如图,在△ABC中,∠C=90°,AC=BC=3,E , F为边AC , BC上的两个动点,且CF=AE , 连接BE , AF , 则BE+AF的最小值为 .
17. 如图,在△ABC中,∠C=90°,AC=BC=3,E , F为边AC , BC上的两个动点,且CF=AE , 连接BE , AF , 则BE+AF的最小值为 .
三、解答题
-
18. 先化简,再求值: ,其中m=2022.19. 如图,点D在△ABC的边BA的延长线上,过AC的中点F作线段GE交∠DAC的平分线于E , 交BC于G , 且AE∥BC .
 (1)、求证:△ABC是等腰三角形;(2)、若AE=8,AB=10,GC=2BG , 求△ABC的周长.20. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)、求证:△ABC是等腰三角形;(2)、若AE=8,AB=10,GC=2BG , 求△ABC的周长.20. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: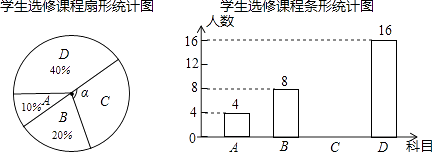 (1)、本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(1)、本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)、请把条形统计图补充完整;(3)、学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
21. 如图,矩形OCBD的顶点O与坐标原点重合,点C在x轴上,点A在对角线OB上,且OA= , .反比例函数 的图象经过点A , 交BC , BD于点M , N , CM= ,连接OM , ON , MN . (1)、求反比例函数 的解析式及点N的坐标;(2)、若点P在x轴上,且△OPN的面积与四边形BMON的面积相等,求点P的坐标.22. 如图,AB是半圆O的直径,C为半圆O上的点(不与A,B重合),连接AC,∠BAC的角平分线交半圆O于点D,过点D作AC的垂线,垂足为E,连接BE交AD于点F.
(1)、求反比例函数 的解析式及点N的坐标;(2)、若点P在x轴上,且△OPN的面积与四边形BMON的面积相等,求点P的坐标.22. 如图,AB是半圆O的直径,C为半圆O上的点(不与A,B重合),连接AC,∠BAC的角平分线交半圆O于点D,过点D作AC的垂线,垂足为E,连接BE交AD于点F.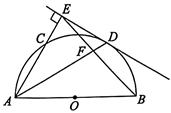 (1)、求证:DE是半圆O的切线;(2)、若AE = 6,半圆O的半径为4,求DF的长.23. 如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)、求证:DE是半圆O的切线;(2)、若AE = 6,半圆O的半径为4,求DF的长.23. 如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.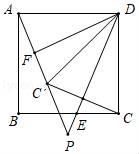 (1)、求∠FDP的度数;(2)、连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;(3)、连接AC,若正方形的边长为 ,请直接写出△ACC′的面积最大值.24. 如图,在平面直角坐标系中,矩形OABC , 点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣ x2+bx+c经过点A和点B .
(1)、求∠FDP的度数;(2)、连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;(3)、连接AC,若正方形的边长为 ,请直接写出△ACC′的面积最大值.24. 如图,在平面直角坐标系中,矩形OABC , 点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣ x2+bx+c经过点A和点B . (1)、求抛物线解析式;(2)、如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE , DE , 若S△BDE=4S△ABE , 求E点坐标;(3)、如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q , 连接AP , AQ , PQ , 若△APQ为直角三角形,请直接写出P点坐标.
(1)、求抛物线解析式;(2)、如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE , DE , 若S△BDE=4S△ABE , 求E点坐标;(3)、如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q , 连接AP , AQ , PQ , 若△APQ为直角三角形,请直接写出P点坐标.