山东省淄博市临淄区2022年中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 温度由 上升 之后是()A、 B、 C、 D、2. 2022年2月1日,微信发布了2022年除夕数据报告,记录了中国老百姓的新年俗报告显示,除夕当天,全国共有6.88亿人参与抢红包,6.88亿用科学记数法可以表示为( )A、 B、 C、 D、3. 如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )
 A、19° B、38° C、42° D、52°4.
A、19° B、38° C、42° D、52°4.如图所示几何体的左视图是( )
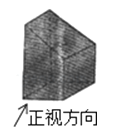 A、
A、 B、
B、 C、
C、 D、
D、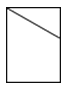 5. 下列运算正确的是( )A、 B、 C、 D、6. 用型号为“大雁牌 ”的计算器计算 ,按键顺序正确的是()A、
5. 下列运算正确的是( )A、 B、 C、 D、6. 用型号为“大雁牌 ”的计算器计算 ,按键顺序正确的是()A、 B、
B、 C、
C、 D、(
D、( 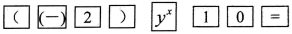 7. 如图, 是 的直径,弦 , , ,则阴影部分图形的面积为( )
7. 如图, 是 的直径,弦 , , ,则阴影部分图形的面积为( )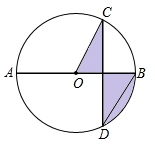 A、 B、 C、 D、8. 如图,已知抛物线 ,将该抛物线在x轴及x轴下方的部分记作 ,将 沿x轴翻折构成的图形记作 ,将 和 构成的图形记作 .关于图形 ,给出的下列四个结论,错误的是()
A、 B、 C、 D、8. 如图,已知抛物线 ,将该抛物线在x轴及x轴下方的部分记作 ,将 沿x轴翻折构成的图形记作 ,将 和 构成的图形记作 .关于图形 ,给出的下列四个结论,错误的是()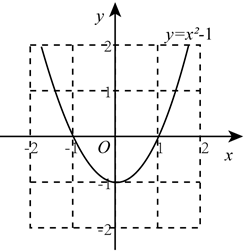 A、图形 恰好经过4个整点(横、纵坐标均为整数的点) B、图形 上任意一点到原点的最大距离是1 C、图形 的周长大于 D、图形 所围成区域的面积大于2且小于9. 已知,关于x的分式方程 有增根,且 ,则 的值是( )A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,矩形ABCO的两边OA , OC落在坐标轴上,反比例函数y= 的图象分别交BC , OB于点D , 点E , 且 ,若S△AOE=3,则k的值为( )
A、图形 恰好经过4个整点(横、纵坐标均为整数的点) B、图形 上任意一点到原点的最大距离是1 C、图形 的周长大于 D、图形 所围成区域的面积大于2且小于9. 已知,关于x的分式方程 有增根,且 ,则 的值是( )A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,矩形ABCO的两边OA , OC落在坐标轴上,反比例函数y= 的图象分别交BC , OB于点D , 点E , 且 ,若S△AOE=3,则k的值为( )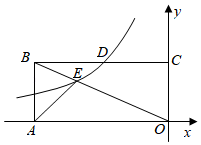 A、﹣4 B、﹣ C、﹣8 D、﹣211. 如图,在 中, , , 平分线与 的垂直平分线交于点 ,将 沿 ( 在 上, 在 上)折叠,点 与点O恰好重合,有如下五个结论:① ;② ;③ 是等边三角形;④ ;⑤ .则上列说法中正确的个数是( )
A、﹣4 B、﹣ C、﹣8 D、﹣211. 如图,在 中, , , 平分线与 的垂直平分线交于点 ,将 沿 ( 在 上, 在 上)折叠,点 与点O恰好重合,有如下五个结论:① ;② ;③ 是等边三角形;④ ;⑤ .则上列说法中正确的个数是( ) A、2 B、3 C、4 D、512. 如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形,第1幅图形中“ ”的个数为 ,第2幅图形中“ ”的个数为 ,第3幅图形中“ ”的个数为 ,…,以此类推,则 的值为( )
A、2 B、3 C、4 D、512. 如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形,第1幅图形中“ ”的个数为 ,第2幅图形中“ ”的个数为 ,第3幅图形中“ ”的个数为 ,…,以此类推,则 的值为( )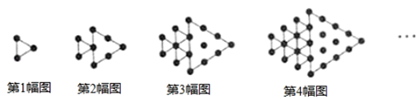 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式5+5x2﹣10x=.14. 有4张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).将这4张纸牌背面朝上洗匀后先由小明从中任意摸出一张,放回洗匀后再由小敏从中任意摸出一张,则“小明所摸纸牌是中心对称图形,小敏所摸纸牌是轴对称图形”的概率为 .
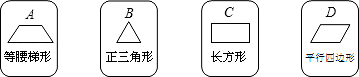 15. 若实数 ,且a、b满足 , ,则代数式 的值为 .16. 对于任意实数a , 抛物线 与x轴至少有一个公共点,则b的取值范围是 .17. 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 .
15. 若实数 ,且a、b满足 , ,则代数式 的值为 .16. 对于任意实数a , 抛物线 与x轴至少有一个公共点,则b的取值范围是 .17. 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 .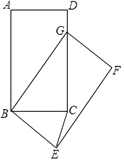
三、解答题
-
18. 已知方程组 的解也是关于x、y的方程 的一个解,求a的值.19. 如图,一次函数y=kx+b(k>0)的图象经过点C(−3,0),且与两坐标轴围成的三角形的面积为3.
 (1)、求一次函数的解析式;(2)、若反比例函数的图象与该一次函数的图象交于一、三象限内的A,B两点,且AC=2BC,求m的值.20. 1月初,某校安排学生在家利用无土栽培技术栽培了10盆花.为了解这些花的情况,该校在4月初对部分学生进行了随机问卷调查,其中一个问题是“这10盆花存活了多少盆?”共有如下四个选项:(A)5盆及以下(B)6盆或7盆(C)8盆或9盆(D)10盆.图1,图2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)、求一次函数的解析式;(2)、若反比例函数的图象与该一次函数的图象交于一、三象限内的A,B两点,且AC=2BC,求m的值.20. 1月初,某校安排学生在家利用无土栽培技术栽培了10盆花.为了解这些花的情况,该校在4月初对部分学生进行了随机问卷调查,其中一个问题是“这10盆花存活了多少盆?”共有如下四个选项:(A)5盆及以下(B)6盆或7盆(C)8盆或9盆(D)10盆.图1,图2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题: (1)、求本次调查的学生总人数,并补全条形统计图;(2)、求扇形统计图中C部分对应的扇形圆心角的度数;(3)、若该校共有2000名学生,请你估计全校可能有多少名学生栽培的花存活了8盆及以上(含8盆)?21. 如图,▱ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)、求本次调查的学生总人数,并补全条形统计图;(2)、求扇形统计图中C部分对应的扇形圆心角的度数;(3)、若该校共有2000名学生,请你估计全校可能有多少名学生栽培的花存活了8盆及以上(含8盆)?21. 如图,▱ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O. (1)、求证:BO=DO;(2)、若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.22. 为迎接建党一百周年,我市计划用两种花卉对某广场进行美化.已知用600元购买A种花卉与用900元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多0.5元.(1)、A,B两种花卉每盆各多少元?(2)、计划购买A,B两种花卉共6000盆,其中A种花卉的数量不超过B种花卉数量的 ,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?23.
(1)、求证:BO=DO;(2)、若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.22. 为迎接建党一百周年,我市计划用两种花卉对某广场进行美化.已知用600元购买A种花卉与用900元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多0.5元.(1)、A,B两种花卉每盆各多少元?(2)、计划购买A,B两种花卉共6000盆,其中A种花卉的数量不超过B种花卉数量的 ,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?23.
阅读理解:
如图1,Rt△ABC中,a , b , c分别是∠A , ∠B , ∠C的对边,∠C=90°,其外接圆半径为R . 根据锐角三角函数的定义:sinA= ,sinB= ,可得 = =c=2R , 即: = = =2R , (规定sin90°=1).
(1)、探究活动:如图2,在锐角△ABC中,a , b , c分别是∠A , ∠B , ∠C的对边,其外接圆半径为R , 那么: 2R(用>、=或<连接),并说明理由 .
(2)、事实上,以上结论适用于任意三角形.初步应用:
在△ABC中,a , b , c分别是∠A , ∠B , ∠C的对边,∠A=60°,∠B=45°,a=8,求b .
(3)、综合应用:如图3,在某次数学活动中,小凤同学测量一古塔CD的高度,在A处用测角仪测得塔顶C的仰角为15°,又沿古塔的方向前行了100m到达B处,此时A , B , D三点在一条直线上,在B处测得塔顶C的仰角为45°,求古塔CD的高度(结果保留小数点后一位).( ≈1.732,sin15°= )
24. 如图,在平面直角坐标系中,抛物线 经过 , 两点. (1)、求抛物线的解析式;(2)、点P是第一象限抛物线上一动点,连接 , 的延长线与x轴交于点Q,过点P作 轴于点E,以 为轴,翻折直线 ,与抛物线相交于另一点R.设P点横坐标为t,R点横坐标为s,求出s与t的函数关系式;(不要求写出自变量t的取值范围);(3)、在(2)的条件下,连接 ,点 在 上,且RG=RC , 连接 ,若 ,求点 坐标.
(1)、求抛物线的解析式;(2)、点P是第一象限抛物线上一动点,连接 , 的延长线与x轴交于点Q,过点P作 轴于点E,以 为轴,翻折直线 ,与抛物线相交于另一点R.设P点横坐标为t,R点横坐标为s,求出s与t的函数关系式;(不要求写出自变量t的取值范围);(3)、在(2)的条件下,连接 ,点 在 上,且RG=RC , 连接 ,若 ,求点 坐标.