山东省淄博市高青县2022年中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 一种商品,先降价10%后又提价10%,现在商品的价格( )A、比原价格高 B、比原价格低 C、与原价格相等 D、无法比较2. 一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
 A、62° B、58° C、52° D、48°3. 如图,在△ABC中,∠C=90°,∠B=42°37',BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A、62° B、58° C、52° D、48°3. 如图,在△ABC中,∠C=90°,∠B=42°37',BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( ) A、
A、
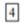


 B、
B、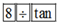
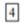


 C、
C、

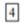


 D、
D、


 4. 下列运算正确的是()A、a3÷a=a2 B、a3•a2=a6 C、(a-b)2=a2-b2 D、(a2)3=a55. 八(3)班七个兴趣小组人数分别为4、4、5、 、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )A、6 B、5 C、4 D、36. 如图,数轴上的三点A , B , C分别表示有理数a , b , c , 则化简|a-b|-|c-a|+|b-c|的结果是( )
4. 下列运算正确的是()A、a3÷a=a2 B、a3•a2=a6 C、(a-b)2=a2-b2 D、(a2)3=a55. 八(3)班七个兴趣小组人数分别为4、4、5、 、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )A、6 B、5 C、4 D、36. 如图,数轴上的三点A , B , C分别表示有理数a , b , c , 则化简|a-b|-|c-a|+|b-c|的结果是( ) A、2a-2c B、0 C、2a-2b D、2b-2c7. △ABC在平面直角坐标系中的位置如图所示,将其绕点P顺时针旋转得到△A'B'C′,则点P的坐标是( )
A、2a-2c B、0 C、2a-2b D、2b-2c7. △ABC在平面直角坐标系中的位置如图所示,将其绕点P顺时针旋转得到△A'B'C′,则点P的坐标是( )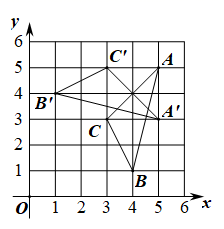 A、(4,5) B、(4,4) C、(3,5) D、(3,4)8. 如图,在圆中半径OC弦AB,且弦AB=CO=2,则图中阴影部分面积为( )
A、(4,5) B、(4,4) C、(3,5) D、(3,4)8. 如图,在圆中半径OC弦AB,且弦AB=CO=2,则图中阴影部分面积为( ) A、 B、 C、 D、9. 如图,在一个长方形中无重叠的放入面积分别为9cm2和8cm2的两张正方形纸片,则图中空白部分的面积为( )
A、 B、 C、 D、9. 如图,在一个长方形中无重叠的放入面积分别为9cm2和8cm2的两张正方形纸片,则图中空白部分的面积为( ) A、 cm2 B、 cm2 C、 cm2 D、 cm210. 如图,点A是双曲线 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线 上运动,则k的值为( )
A、 cm2 B、 cm2 C、 cm2 D、 cm210. 如图,点A是双曲线 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线 上运动,则k的值为( ) A、1 B、2 C、3 D、411. 如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作BA1⊥AC , 过A1作A1B1⊥BC , 再过B1作B1A2⊥AC , 然后过A2作A2B2⊥BC , …如此下去,则AnBn的长为( )
A、1 B、2 C、3 D、411. 如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作BA1⊥AC , 过A1作A1B1⊥BC , 再过B1作B1A2⊥AC , 然后过A2作A2B2⊥BC , …如此下去,则AnBn的长为( ) A、 B、 C、 D、12. 如图,在 中, , , 为 边上的一个动点(不与 、 重合),连接 ,则 的最小值是( )
A、 B、 C、 D、12. 如图,在 中, , , 为 边上的一个动点(不与 、 重合),连接 ,则 的最小值是( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
13. 一们同学在解关于x的分式方程 的过程中产生了增根,则可以推断a的值为 .14. 把多项式 分解因式的结果是 .15. 把抛物线y=x2+1关于x轴对称,所得到的抛物线解析式为 .16. 如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP , 点C关于直线BP的对称点为 ,连接C .当点P运动时,点 也随之运动.若点P从点A运动到点D , 则线段C 扫过的区域的面积是 .
 17. 已知点A(2,4),B(0,1),点M在抛物线y= x2上运动,则AM+BM的最小值为 .
17. 已知点A(2,4),B(0,1),点M在抛物线y= x2上运动,则AM+BM的最小值为 .三、解答题
-
18. 先化简,再求值: , 其中a.19. 如图,在△ABC中,AD⊥BC , BE⊥AC , 垂足分别为D , E , AD与BE相交于点F .
 (1)、求证:△ACD∽△BFD;(2)、当tan∠ABD=1,BF=4时,求AC的长.20. 教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到9小时.为了解学生每天的睡眠时间,学校随机调查了部分学生,将学生睡眠时间分为A , B , C , D四组(每名学生必须选择且只能选择一种情况):
(1)、求证:△ACD∽△BFD;(2)、当tan∠ABD=1,BF=4时,求AC的长.20. 教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到9小时.为了解学生每天的睡眠时间,学校随机调查了部分学生,将学生睡眠时间分为A , B , C , D四组(每名学生必须选择且只能选择一种情况):A组:睡眠时间<8小时; B组:8小时≤睡眠时间<9小时;
C组:9小时≤睡眠时间<10小时; D组:睡眠时间≥10小时;
如图1和图2是根据调查结果绘制的不完整的统计图,请根据图中提供的信息,解答下列问题:
 (1)、被调查的学生有人;(2)、补全条形统计图;(3)、请估计全校800名学生中睡眠时间不足9小时的人数.21. 如图,直线y=ax+1与x轴、y轴分别相交于A , B两点,与双曲线y= (x>0)相交于点P , PC⊥x轴于点C , 且PC=2,tan∠BAO= .
(1)、被调查的学生有人;(2)、补全条形统计图;(3)、请估计全校800名学生中睡眠时间不足9小时的人数.21. 如图,直线y=ax+1与x轴、y轴分别相交于A , B两点,与双曲线y= (x>0)相交于点P , PC⊥x轴于点C , 且PC=2,tan∠BAO= . (1)、求一次函数系数a的值;(2)、求双曲线的解析式;(3)、若点Q为双曲线上点P右侧一点,且QH⊥x轴于H , 当以点Q , C , H为顶点的三角形与△AOB相似时,求点Q的坐标.22. 为庆祝建党100周年,某银行发行了A、B两种纪念币,已知3枚A型纪念币和2枚B型纪念币面值共需55元,6枚A型纪念币和5枚B型纪念币共需130元.(1)、求每枚A、B两种型号的纪念币面值各多少元?(2)、若小明准备用至少850元的金额购买两种纪念币共50枚,求A型纪念币最多能采购多少枚?(3)、在(2)的条件下,若小明至少要购买A型纪念币8枚,则共有几种购买方案,请罗列出来,哪种方案最划算?23. 如图,菱形ABCD与菱形GECF的顶点C重合,∠BCD=∠ECF=60°,已知菱形GECF绕点C旋转的角度为α .
(1)、求一次函数系数a的值;(2)、求双曲线的解析式;(3)、若点Q为双曲线上点P右侧一点,且QH⊥x轴于H , 当以点Q , C , H为顶点的三角形与△AOB相似时,求点Q的坐标.22. 为庆祝建党100周年,某银行发行了A、B两种纪念币,已知3枚A型纪念币和2枚B型纪念币面值共需55元,6枚A型纪念币和5枚B型纪念币共需130元.(1)、求每枚A、B两种型号的纪念币面值各多少元?(2)、若小明准备用至少850元的金额购买两种纪念币共50枚,求A型纪念币最多能采购多少枚?(3)、在(2)的条件下,若小明至少要购买A型纪念币8枚,则共有几种购买方案,请罗列出来,哪种方案最划算?23. 如图,菱形ABCD与菱形GECF的顶点C重合,∠BCD=∠ECF=60°,已知菱形GECF绕点C旋转的角度为α . (1)、如图①,当点G在对角线AC上时,求 的值;(2)、如图②,当菱形GECF按顺时针方向旋转的角度为α(0°<α<60°),探索线段AG与BE之间的数量关系,并证明你的结论;(3)、如图③,在菱形GECF旋转的过程中,当点A , G , F在同一条直线上时,连接CG并延长,交AD于点H , 若CE=2,GH= ,求AH的长.24. 如图,抛物线y=﹣x2+bx+c过点A(﹣1,0)和点B(3,0),与y轴交于点C在x轴上有一动点E(m , 0)(其中m为实数,0<m<3),过动点E作直线l⊥x轴,交抛物线于点M .
(1)、如图①,当点G在对角线AC上时,求 的值;(2)、如图②,当菱形GECF按顺时针方向旋转的角度为α(0°<α<60°),探索线段AG与BE之间的数量关系,并证明你的结论;(3)、如图③,在菱形GECF旋转的过程中,当点A , G , F在同一条直线上时,连接CG并延长,交AD于点H , 若CE=2,GH= ,求AH的长.24. 如图,抛物线y=﹣x2+bx+c过点A(﹣1,0)和点B(3,0),与y轴交于点C在x轴上有一动点E(m , 0)(其中m为实数,0<m<3),过动点E作直线l⊥x轴,交抛物线于点M . (1)、求抛物线解析式及点C的坐标;(2)、当m=1时,在直线l上是否存在第一象限内的点D , 使得△ACD是以∠DCA为底角的等腰三角形,若存在,求点D的坐标,若不存在,请说明理由;(3)、连接BM并延长交y轴于点N , 连接AM , OM若△AEM的面积等于△MON面积的2倍,求m的值.
(1)、求抛物线解析式及点C的坐标;(2)、当m=1时,在直线l上是否存在第一象限内的点D , 使得△ACD是以∠DCA为底角的等腰三角形,若存在,求点D的坐标,若不存在,请说明理由;(3)、连接BM并延长交y轴于点N , 连接AM , OM若△AEM的面积等于△MON面积的2倍,求m的值.