山东省淄博市博山区2022年九年级数学一模试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 冬季奥林匹克运动会(简称冬奥会)是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会将于2022年2月4日在北京开幕、下列四个图分别是四届冬奥会图标中的一部分,其中不是轴对称图形的为()A、
 B、
B、 C、
C、 D、
D、 2. 为抗击新冠肺炎,国家大力提高口罩产能,据统计,我国一月份口罩产量达到42亿只,42亿用科学记数法表示为()A、 B、 C、 D、3. 下列语句正确的是().A、延长射线AB B、线段MN叫做点M , N间的距离 C、两点之间,直线最短 D、直线a , b相交于点P4. 下列运算正确的是()A、 B、 C、 D、5. 如图,直线 ,点 分别在直线 上,P为两平行线间一点,那么 等于( )
2. 为抗击新冠肺炎,国家大力提高口罩产能,据统计,我国一月份口罩产量达到42亿只,42亿用科学记数法表示为()A、 B、 C、 D、3. 下列语句正确的是().A、延长射线AB B、线段MN叫做点M , N间的距离 C、两点之间,直线最短 D、直线a , b相交于点P4. 下列运算正确的是()A、 B、 C、 D、5. 如图,直线 ,点 分别在直线 上,P为两平行线间一点,那么 等于( ) A、 B、 C、 D、6. 若 是关于x的一元一次方程 的解,则 的值是()A、7 B、8 C、 D、7. 如图, , 都是等边三角形,则作 的度数是( )
A、 B、 C、 D、6. 若 是关于x的一元一次方程 的解,则 的值是()A、7 B、8 C、 D、7. 如图, , 都是等边三角形,则作 的度数是( ) A、 B、 C、 D、8. 已知点 在x轴上,点 在y轴上,则点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在平面直角坐标系中,半径为5的 与y轴交于点 , ,与x轴交于C,D,则点D的坐标为( )
A、 B、 C、 D、8. 已知点 在x轴上,点 在y轴上,则点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在平面直角坐标系中,半径为5的 与y轴交于点 , ,与x轴交于C,D,则点D的坐标为( ) A、 B、 C、 D、10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
A、 B、 C、 D、10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )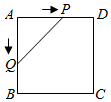 A、
A、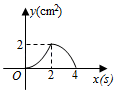 B、
B、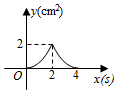 C、
C、 D、
D、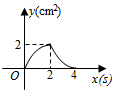 11. “行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.在某路口的斑马线路段 横穿双向车道,其中, 米,在人行绿灯亮时,小刚共用时10秒通过 ,其中通过 的速度是通过 的1.3倍,求小刚通过 的速度.设小刚通过 的速度为x米/秒,则根据题意列方程为( )
11. “行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.在某路口的斑马线路段 横穿双向车道,其中, 米,在人行绿灯亮时,小刚共用时10秒通过 ,其中通过 的速度是通过 的1.3倍,求小刚通过 的速度.设小刚通过 的速度为x米/秒,则根据题意列方程为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,直线 分别与x轴、y轴相交于点A、B,点E、F分别是正方形 的边 、 上的动点,且 ,过原点O作 ,垂足为H,连接 、 ,则 面积的最大值为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,直线 分别与x轴、y轴相交于点A、B,点E、F分别是正方形 的边 、 上的动点,且 ,过原点O作 ,垂足为H,连接 、 ,则 面积的最大值为( ) A、 B、12 C、 D、
A、 B、12 C、 D、二、填空题
-
13. 若方程 (其中a,b,c为常数且 )的两个实数根分别为 , ,则 , . (用a,b,c表示)14. 分解因式: .15. 从小到大排列的一组数 ,如果这组数据的平均数与中位数相等,则 的值为 .16. 如图,在 中, ,若以点A为圆心, 半径的弧交 于点E , 以B为圆心, 为半径的弧交 于点D , 则图中阴影部分图形的面积为 .
 17. 如图,在平面直角坐标系中,等腰直角三角形 的直角边 在x轴上,点 在第一象限,且 ,以点 为直角顶点, 为一直角边作等腰直角三角形 ,再以点 为直角顶点, 为直角边作等腰直角三角形 ……依此规律,则点 的坐标是 .
17. 如图,在平面直角坐标系中,等腰直角三角形 的直角边 在x轴上,点 在第一象限,且 ,以点 为直角顶点, 为一直角边作等腰直角三角形 ,再以点 为直角顶点, 为直角边作等腰直角三角形 ……依此规律,则点 的坐标是 .
三、解答题
-
18. 解不等式组并把解表示在数轴上.
 19. 已知如图,四边形ABCD是平行四边形.
19. 已知如图,四边形ABCD是平行四边形. (1)、尺规作图:作∠ABC的角平分线交CD的延长线于E , 交AD于F(不写作法和证明,但要保留作图痕迹).(2)、请在(1)的情况下,求证:DE=DF .20. 2022北京冬残奥会是历史上第13届冬残奥会,于2022年3月4日至3月13日举行.比赛共设6个大项,即残奥高山滑雪、残奥冬季两项、残奥越野滑雪、残奥单板滑雪、残奥冰球、轮椅冰壶.小明为了解同学们是否知晓这6大项目,随机对学校的部分同学进行了一次问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个类别,根据调查结果,绘制出如图所示的条形统计图和扇形统计图.
(1)、尺规作图:作∠ABC的角平分线交CD的延长线于E , 交AD于F(不写作法和证明,但要保留作图痕迹).(2)、请在(1)的情况下,求证:DE=DF .20. 2022北京冬残奥会是历史上第13届冬残奥会,于2022年3月4日至3月13日举行.比赛共设6个大项,即残奥高山滑雪、残奥冬季两项、残奥越野滑雪、残奥单板滑雪、残奥冰球、轮椅冰壶.小明为了解同学们是否知晓这6大项目,随机对学校的部分同学进行了一次问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个类别,根据调查结果,绘制出如图所示的条形统计图和扇形统计图.

请根据图表中的信息回答下列问题:
(1)、求本次调查的样本容量.(2)、求图中a的值.(3)、求图“基本了解”类别所对应的圆心角大小.(4)、若某同学对项目了解类别为“非常了解”或者“比较了解”的话,则可称为“奥知达人”,现从该校随机抽查1名学生,求该学生是“奥知达人”的概率.21. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线.为了测量房屋的高度,在地面上C点测得屋顶 的仰角为 ,此时地面上C点、屋檐上 点、屋顶上A点三点恰好共线,继续向房屋方向走 到达点D时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点G(点C,D, 在同一水平线上).(参考数据: , , , )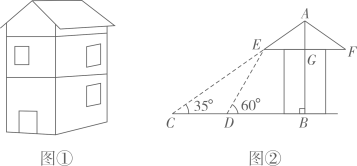 (1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).22. 如图,正六边形ABCDEF的对称中心P在反比例函数 的图象上,边CD在x轴上,点B在y轴上,已知CD=4.
(1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).22. 如图,正六边形ABCDEF的对称中心P在反比例函数 的图象上,边CD在x轴上,点B在y轴上,已知CD=4. (1)、点A是否在该反比例函数的图象上?请说明理由;(2)、若反比例函数的图象与DE交于点Q , 求点Q的横坐标.23. 如图,在 中, , ,点P是 边上一动点,作 于点D,连接 ,把 绕点A逆时针旋转 ,得到 ,连接 , , .
(1)、点A是否在该反比例函数的图象上?请说明理由;(2)、若反比例函数的图象与DE交于点Q , 求点Q的横坐标.23. 如图,在 中, , ,点P是 边上一动点,作 于点D,连接 ,把 绕点A逆时针旋转 ,得到 ,连接 , , . (1)、求证:四边形 是矩形;(2)、如图2所示,当点P运动 的延长线上时, 与 交于点F,其他条件不变, 已知 ,求 的值;(3)、点P在 边上运动的过程中,线段 上存在一点Q,使 的值最小,当 的值取得最小值时,若 的长为2,求 的长.24. 如图,已知抛物线 与x轴交于A,B两点,与y轴交于点C,且点A的坐标为 ,直线 的解析式为 .
(1)、求证:四边形 是矩形;(2)、如图2所示,当点P运动 的延长线上时, 与 交于点F,其他条件不变, 已知 ,求 的值;(3)、点P在 边上运动的过程中,线段 上存在一点Q,使 的值最小,当 的值取得最小值时,若 的长为2,求 的长.24. 如图,已知抛物线 与x轴交于A,B两点,与y轴交于点C,且点A的坐标为 ,直线 的解析式为 . (1)、求抛物线的解析式;(2)、如图1,过点A作 交抛物线于点D(异于点A),P是直线 下方抛物线上一点,过点P作 轴,交 于点Q,过点Q作 于点R,连接 .求 面积的最大值及此时点P的坐标;(3)、如图2,点C关于 轴的对称点为点 ,将抛物线沿射线 的方向平移 个单位长度得到新的抛物线 ,新抛物线 与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,过点A作 交抛物线于点D(异于点A),P是直线 下方抛物线上一点,过点P作 轴,交 于点Q,过点Q作 于点R,连接 .求 面积的最大值及此时点P的坐标;(3)、如图2,点C关于 轴的对称点为点 ,将抛物线沿射线 的方向平移 个单位长度得到新的抛物线 ,新抛物线 与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.