山东省枣庄市台儿庄区2022年中考一模数学试题

试卷更新日期：2022-05-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（　　）

A、 $3 a^{2} + 4 a^{2} = 7 a^{4}$ B、 $\sqrt{a^{2}} \cdot \frac{1}{a} = 1$ C、 $- 18 + 12 \div (- \frac{3}{2}) = 4$ D、 $\frac{a^{2}}{a - 1} - a - 1 = \frac{1}{a - 1}$

查看试题解析
2. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $a$ ， $b$ 是等腰三角形的两边长，且a，b满足 $\sqrt{2 a - 3 b + 5} + {(2 a + 3 b - 13)}^{2} = 0$ ，则此等腰三角形的周长为（）．

A、8 B、6或8 C、7 D、7或8

查看试题解析
4. 关于 $x$ 的方程 ${(k - 1)}^{2} x^{2} + (2 k + 1) x + 1 = 0$ 有实数根，则k的取值范围是（）

A、 $k > \frac{1}{4}$ 且 $k \neq 1$ B、 $k \geq \frac{1}{4}$ 且 $k \neq 1$ C、 $k > \frac{1}{4}$ D、 $k \geq \frac{1}{4}$

查看试题解析
5. 若关于x的不等式组 ${\begin{array}{l} 2 x + 3 > 12 \\ x - a \leq 0 \end{array}$ 恰有3个整数解，则实数a的取值范围是（）

A、 $7 < a < 8$ B、 $7 < a \leq 8$ C、 $7 \leq a < 8$ D、 $7 \leq a \leq 8$

查看试题解析
6. 如图，点B ， F ， C ， E共线，∠B=∠E ， BF=EC ，添加一个条件，不能判断△ABC≌△DEF的是（）

A、AB=DE B、∠A=∠D C、AC=DF D、AC∥FD

查看试题解析
7. 如图，已知抛物线 $y = a x^{2} + c$ 与直线 $y = k x + m$ 交于 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ 两点，则关于 $x$ 的不等式 $a x^{2} + c \geq - k x + m$ 的解集是（）

A、 $x \leq - 3$ 或 $x \geq 1$ B、 $x \leq - 1$ 或 $x \geq 3$ C、 $- 3 \leq x \leq 1$ D、 $- 1 \leq x \leq 3$

查看试题解析
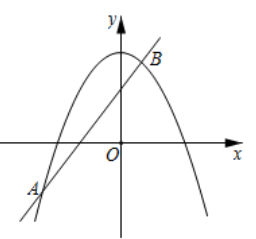8. 一个骰子相对两面的点数之和为7，它的展开图如图，下列判断正确的是（）

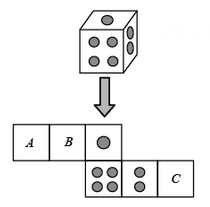A、 $A$ 代表 B、 $B$ 代表 C、 $C$ 代表 D、 $B$ 代表

查看试题解析
9. 如图，在Rt $△$ ABC中，∠C＝90°，AB＝5，点O在AB上，OB＝2，以OB为半径的⊙O与AC相切于点D ，交BC于点E ，则CE的长为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析
10. 如图，在平面直角坐标系中，菱形 $A B C D$ 的边 $B C$ 与x轴平行，A ， B两点纵坐标分别为4，2，反比例函数 $y = \frac{k}{x}$ 经过A ， B两点，若菱形 $A B C D$ 面积为8，则k值为（）

A、 $- 8 \sqrt{3}$ B、 $- 2 \sqrt{3}$ C、 $- 8$ D、 $- 6 \sqrt{3}$

查看试题解析

二、填空题

11. 计算： ${(- \frac{1}{2})}^{- 2} + {(π - 3.14)}^{0} + 4 \cos 45^{\circ} - | 1 - \sqrt{2} | =$ ．

查看试题解析
12. 如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为 $A B$ 、 $C D$ ，若 $C D // B E$ ， $∠ 1 =20 °$ ，则 $∠ 2$ 的度数是.

查看试题解析
13. 在一个不透明的袋中装有除颜色外其余都相同的5个小球，其中3个红球、2个黄球．如果第一次先从袋中摸出1个球后不放回，第二次再从袋中摸出1个球，那么两次都摸到黄球的概率是．

查看试题解析
14. 如图，在边长为4的正方形 $A B C D$ 中，以 $A B$ 为直径的半圆交对角线 $A C$ 于点E，以C为圆心、 $B C$ 长为半径画弧交 $A C$ 于点F，则图中阴影部分的面积是.

查看试题解析
15. 如图，在菱形ABCD中，AB＝AC＝10，对角线AC、BD相交于点O ，点M在线段AC上，且AM＝3，点P为线段BD上的一个动点，则MP+ $\frac{1}{2}$ PB的最小值是．

查看试题解析
16. 观察下列一组数：﹣ $\frac{2}{3}$ ， $\frac{6}{9}$ ，﹣ $\frac{12}{27}$ ， $\frac{20}{81}$ ，﹣ $\frac{30}{243}$ ，…，它们是按一定规律排列的，那么这一组数的第n个数是.

查看试题解析

三、解答题

17. 先化简，再求值： $\frac{m^{3} - 2 m^{2}}{m^{2} - 4 m + 4} \div (\frac{9}{m - 3} + m + 3)$ ，其中m是已知两边分别为2和3的三角形的第三边长，且m是整数.

查看试题解析

18. 疫苗接种初期，为更好地响应国家对符合条件的人群接种新冠疫苗的号召，某市教育部门随机抽取了该市部分七、八、九年级教师，了解教师的疫苗接种情况，得到如下统计表：

	已接种	未接种	合计
七年级	30	10	40
八年级	35	15	$a$
九年级	40	$b$	60
合计	105	$c$	150

(1)、表中，

a =

，

b =

，

c =

；

(2)、由表中数据可知，统计的教师中接种率最高的是年级教师；（填“七”或“八”或“九”）

(3)、若该市初中七、八、九年级一共约有8000名教师，根据抽样结果估计未接种的教师约有人；

(4)、为更好地响应号召，立德中学从最初接种的4名教师（其中七年级1名，八年级1名，九年级2名）中随机选取2名教师谈谈接种的感受，请用列表或画树状图的方法，求选中的两名教师恰好不在同一年级的概率.

查看试题解析

19. 已知：如图，矩形 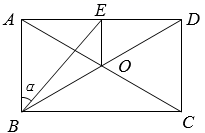$A B C D$ 的对角线 $A C ， B D$ 相交于点O， $∠ B O C = 120 ° ， A B = 2$ .

(1)、求矩形对角线的长.

(2)、过O作 $O E ⊥ A D$ 于点E，连结BE.记 $∠ A B E = α$ ，求 $tan α$ 的值.

查看试题解析
20. 如图，矩形 $A B C D$ 的两边 $A B ， B C$ 的长分别为3，8，C ， D在y轴上，E是 $A D$ 的中点，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点E ，与 $B C$ 交于点F ，且 $C F - B E = 1$ ．

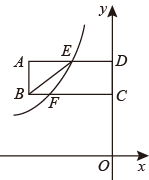(1)、求反比例函数的解析式；

(2)、在y轴上找一点P ，使得 $S_{△ C E P} = \frac{2}{3} S_{矩形 A B C D}$ ，求此时点P的坐标．

查看试题解析
21. 国庆节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售.经了解，甲种水果和乙种水果的进价与售价如下表所示：

水果单价

甲

乙

进价（元/千克）

$x$

$x + 4$

售价（元/千克）

20

25

已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.

(1)、求 $x$ 的值；

(2)、若超市购进这两种水果共100千克，其中甲种水果的重量不低于乙种水果重量的3倍，则超市应如何进货才能获得最大利润，最大利润是多少？

查看试题解析
22. 已知 $△$ AOB和 $△$ MON都是等腰直角三角形（ $\frac{\sqrt{2}}{2}$ OA＜OM＜OA），∠AOB＝∠MON＝90°．

(1)、如图1，连接AM ， BN ，求证：AM＝BN；

(2)、将 $△$ MON绕点O顺时针旋转．如图2，当点M恰好在AB边上时，求证：AM²+BM²＝2OM²；

查看试题解析
23. 如图1，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD.

(1)、判断直线CD与⊙O的位置关系，并说明理由；

(2)、若tan∠ADC＝ $\frac{1}{2}$ ，AC＝2，求⊙O的半径；

(3)、如图2，在（2）的条件下，∠ADB的平分线DE交⊙O于点E，交AB于点F，连结BE.求sin∠DBE的值.

查看试题解析
24. 如图，在平面直角坐标系xOy中，抛物线 $y = - \frac{1}{4} x^{2} + \frac{3}{2} x + 4$ 与两坐标轴分别相交于A ， B ， C三点

(1)、求证：∠ACB=90°

(2)、点D是第一象限内该抛物线上的动点，过点D作x轴的垂线交BC于点E ，交x轴于点F ．
①求DE+BF的最大值；

②点G是AC的中点，若以点C ， D ， E为顶点的三角形与 $△$ AOG相似，求点D的坐标．

查看试题解析

水果单价	甲	乙
进价（元/千克）	$x$	$x + 4$
售价（元/千克）	20	25