山东省潍坊市潍城区2022年中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
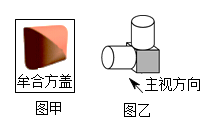
1. 的平方根为()A、 B、 C、 D、2. 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是()
 A、
A、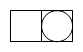
B、
B、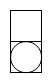
C、
C、
D、
D、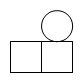
3. 2021年,太原卫星发射中心发射了“羲和号”太阳双超卫星,拉开了太阳空间探测的序幕.太阳是人类目前唯一可进行高时空分辨率和高光谱分辨率观测的恒星,它距地球约1.5亿公里,直径约139万公里,质量是地球的33万倍.用科学记数法表示数据139万公里,并精确到十万位,则表示正确的为()A、 公里 B、 公里 C、 公里 D、 公里4. 将多项式因式分解,结果正确的是( )A、 B、 C、 D、5. 在 中, ,P是射线 上一动点,当 时, 的长为( )A、4 B、8 C、4或8 D、4或6. 某数学兴趣小组做小球弹跳实验.将小球扔下,该小球反复地弹离地面,直到它停下.下面的图象刻画了小球弹跳过程中球离地面的高度和时间之间的关系.此过程中,小球有()次距离地面0.45米.
3. 2021年,太原卫星发射中心发射了“羲和号”太阳双超卫星,拉开了太阳空间探测的序幕.太阳是人类目前唯一可进行高时空分辨率和高光谱分辨率观测的恒星,它距地球约1.5亿公里,直径约139万公里,质量是地球的33万倍.用科学记数法表示数据139万公里,并精确到十万位,则表示正确的为()A、 公里 B、 公里 C、 公里 D、 公里4. 将多项式因式分解,结果正确的是( )A、 B、 C、 D、5. 在 中, ,P是射线 上一动点,当 时, 的长为( )A、4 B、8 C、4或8 D、4或6. 某数学兴趣小组做小球弹跳实验.将小球扔下,该小球反复地弹离地面,直到它停下.下面的图象刻画了小球弹跳过程中球离地面的高度和时间之间的关系.此过程中,小球有()次距离地面0.45米. A、2 B、3 C、4 D、57. 等腰三角形边长分别为a , b , 2,且a , b是关于x的一元二次方程 的两个根,则n的值为( )A、7 B、8 C、7或8 D、8或98. “莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形,转子发动机的设计就是利用了莱洛三角形.它是分别以正三角形的顶点为圆心,以其边长为半径作弧形成的图形,如图2所示.若正三角形的边长为3,则该“莱洛三角形”的面积为( )
A、2 B、3 C、4 D、57. 等腰三角形边长分别为a , b , 2,且a , b是关于x的一元二次方程 的两个根,则n的值为( )A、7 B、8 C、7或8 D、8或98. “莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形,转子发动机的设计就是利用了莱洛三角形.它是分别以正三角形的顶点为圆心,以其边长为半径作弧形成的图形,如图2所示.若正三角形的边长为3,则该“莱洛三角形”的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列调查中,适合用全面调查的是()A、调查黄河的水质情况 B、调查全国中学生的心理健康状况 C、调查某班级40名学生的视力情况 D、某客运公司检测10辆客运汽车的安全性能10. 关于x的分式方程 解的情况,下列说法正确的是().A、若 ,则此方程无解 B、若 ,则此方程无解 C、若方程的解为负数,则 D、若 ,则方程的解为正数11. 如图,已知 ,点E , F分别在直线 上,且 平分 平分 , 与 相交于点O , 则下列结论正确的是( )
 A、 B、 C、 D、12. 在同一平面直角坐标系中,如图所示,正比例函数 与一次函数 的图象则二次函数 的图象可能是()
A、 B、 C、 D、12. 在同一平面直角坐标系中,如图所示,正比例函数 与一次函数 的图象则二次函数 的图象可能是() A、
A、 B、
B、 C、
C、 D、
D、
三、填空题
-
13. 计算 的结果是 .14. 云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的.下图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图,该场地可以看作是从一个长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为 ,其边缘 ,点E在 上, .一名滑雪爱好者从点A滑到点E , 他滑行的最短路线长为m .
 15. 如图是一张四边形纸片 , , , , ,点M , N分别是 , 上的点,将 沿直线 翻折,将 沿直线 翻折,点A和点B落在同一点G处,再将纸片沿直线 折叠,点C恰好落在点D处,则 的长为 .
15. 如图是一张四边形纸片 , , , , ,点M , N分别是 , 上的点,将 沿直线 翻折,将 沿直线 翻折,点A和点B落在同一点G处,再将纸片沿直线 折叠,点C恰好落在点D处,则 的长为 . 16. 如图,在平面直角坐标系中,点B的坐标为 , 轴,反比例函数 的图象与 交于点C , 与 交于点E , 且 , ,则点E的坐标为 .
16. 如图,在平面直角坐标系中,点B的坐标为 , 轴,反比例函数 的图象与 交于点C , 与 交于点E , 且 , ,则点E的坐标为 . 17. 先化简,再求值: ,其中a为不等式组 的整数解.18. 某移动公司为了提升网络信号,在坡度 的山坡 上加装了信号塔 (如图所示),信号塔底端Q到坡底A的距离为3.9米.为了提醒市民,在距离斜坡底A点5.4米的水平地面上立了一块警示牌 ,当太阳光线与水平线所成的夹角为 时,信号塔顶端P的影子落在警示牌上的点E处,且 长为3米.
17. 先化简,再求值: ,其中a为不等式组 的整数解.18. 某移动公司为了提升网络信号,在坡度 的山坡 上加装了信号塔 (如图所示),信号塔底端Q到坡底A的距离为3.9米.为了提醒市民,在距离斜坡底A点5.4米的水平地面上立了一块警示牌 ,当太阳光线与水平线所成的夹角为 时,信号塔顶端P的影子落在警示牌上的点E处,且 长为3米. (1)、求点Q到水平地面的铅直高度;(2)、求信号塔 的高度大约为多少米?(参考数据: )19. 某商场为掌握国庆节期间顾客购买商品时刻的分布情况,统计了10月1日7:00-23:00这一时间段内5000名顾客的购买时刻.顾客购买商品时刻的频数分布直方图和扇形统计图如图所示,将7:00-23:00这一时间段划分为四个小的时间段:A段为 ,B段为 ,C段为 ,D段为 ,其中t为顾客购买商品的时刻,扇形统计图中,A , B , C , D四段各部分圆心角的度数比为1∶3∶4∶2.
(1)、求点Q到水平地面的铅直高度;(2)、求信号塔 的高度大约为多少米?(参考数据: )19. 某商场为掌握国庆节期间顾客购买商品时刻的分布情况,统计了10月1日7:00-23:00这一时间段内5000名顾客的购买时刻.顾客购买商品时刻的频数分布直方图和扇形统计图如图所示,将7:00-23:00这一时间段划分为四个小的时间段:A段为 ,B段为 ,C段为 ,D段为 ,其中t为顾客购买商品的时刻,扇形统计图中,A , B , C , D四段各部分圆心角的度数比为1∶3∶4∶2.
请根据上述信息解答下列问题:
(1)、通过计算将频数直方图补充完整,并直接写出顾客购买商品时刻的中位数落在哪个时间段?(2)、求10月1日这天顾客购买商品时刻的平均值(同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表例如,A段的中点值为: );(3)、为活跃节日气氛,该商场设置购物后抽奖活动,设立了特等奖一个,一等奖两个,二等奖若干,并随机分配到A , B , C , D四个时间段中.①请直接写出特等奖出现在A时间段的概率;
②请利用画树状图或列表的方法,求两个一等奖出现在不同时间段的概率.
20. 如图,以 的边 为直径的 交 于点F , 点E是 的中点,连接 并延长交 于点D , 若 . (1)、求证: 是 的切线;(2)、若 的半径为2, ,求 的长.21. 某公司生产的一种产品在市场上很受欢迎,该公司每年的产量为6万件,可在国内和国外两个市场全部销售.若在国外销售,平均每件产品的利润 (元)与国外销售量x(万件)之间的函数关系如图所示.若在国内销售,平均每件产品的利润为 元,设该公司每年在国内和国外销售的总利润为w万元.
(1)、求证: 是 的切线;(2)、若 的半径为2, ,求 的长.21. 某公司生产的一种产品在市场上很受欢迎,该公司每年的产量为6万件,可在国内和国外两个市场全部销售.若在国外销售,平均每件产品的利润 (元)与国外销售量x(万件)之间的函数关系如图所示.若在国内销售,平均每件产品的利润为 元,设该公司每年在国内和国外销售的总利润为w万元. (1)、求 与x之间的函数表达式,并写出x的取值范围;(2)、该公司每年在国内国外销售量各为多少时,可使公司每年的总利润最大?最大总利润是多少?22. 如图①,二次函数 经过菱形 的顶点A , B , D , 且 ,点D的坐标为(0,4),延长 交抛物线于另一点E , 连接 ,交 于点F .
(1)、求 与x之间的函数表达式,并写出x的取值范围;(2)、该公司每年在国内国外销售量各为多少时,可使公司每年的总利润最大?最大总利润是多少?22. 如图①,二次函数 经过菱形 的顶点A , B , D , 且 ,点D的坐标为(0,4),延长 交抛物线于另一点E , 连接 ,交 于点F . (1)、求二次函数的表达式;(2)、求 的面积;(3)、如图②,直线l是二次函数图象的对称轴,若P为l上一点,且P , D , B三点构成以 为底的等腰三角形,求点P的坐标.23. 如图,矩形 中, 为等边三角形.点E , F分别为 边上的动点,且 ,P为 上一动点,连接 ,将线段 绕点B顺时针旋转 至 ,连接 .
(1)、求二次函数的表达式;(2)、求 的面积;(3)、如图②,直线l是二次函数图象的对称轴,若P为l上一点,且P , D , B三点构成以 为底的等腰三角形,求点P的坐标.23. 如图,矩形 中, 为等边三角形.点E , F分别为 边上的动点,且 ,P为 上一动点,连接 ,将线段 绕点B顺时针旋转 至 ,连接 . (1)、求证: ;(2)、当 三条线段的和最小时,求 的长;(3)、若点E以每秒2个单位的速度由A点向D点运动,点P以每秒1个单位的速度由E点向F点运动.E , P两点同时出发,点E到达点D时停止,点P到达点F时停止,设点P的运动时间为t秒.
(1)、求证: ;(2)、当 三条线段的和最小时,求 的长;(3)、若点E以每秒2个单位的速度由A点向D点运动,点P以每秒1个单位的速度由E点向F点运动.E , P两点同时出发,点E到达点D时停止,点P到达点F时停止,设点P的运动时间为t秒.①求t为何值时, 与 相似;
②求 的面积S的最小值.