山东省威海乳山市2022年中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、5 C、 D、2. 对于下图所示的几何体,正确的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 据报道,在中国科研团队在联合攻关下,成功构建76个光子的量子计算原型机“九章”.实验显示,当求解5000万个样本的高斯玻色取样时,“九章”仅需200秒.从运算等效来看,“九章”的计算用时仅为“悬铃木”用时的百亿分之一.“百亿分之一”用科学记数法可以表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. “玉兔”在月球表面行走的动力主要来自于太阳光能,要使接收太阳光能最多,就要使光线垂直照射在太阳光板上.某一时刻太阳光的照射角度如图所示,要使得此时接收的光能最多,那么太阳光板绕支点A逆时针旋转的最小角度为( )
3. 据报道,在中国科研团队在联合攻关下,成功构建76个光子的量子计算原型机“九章”.实验显示,当求解5000万个样本的高斯玻色取样时,“九章”仅需200秒.从运算等效来看,“九章”的计算用时仅为“悬铃木”用时的百亿分之一.“百亿分之一”用科学记数法可以表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. “玉兔”在月球表面行走的动力主要来自于太阳光能,要使接收太阳光能最多,就要使光线垂直照射在太阳光板上.某一时刻太阳光的照射角度如图所示,要使得此时接收的光能最多,那么太阳光板绕支点A逆时针旋转的最小角度为( ) A、 B、 C、 D、6. 在数轴上,点A , B表示的数分别是 和2,则线段AB的中点表示的数是( )A、 B、 C、 D、7. 化简 的结果是( )A、 B、 C、 D、8. 如图,四边形ABCD和AECF都是菱形,点E , F在对角线BD上,∠ABC=60°,∠AEC=120°, ,则AB=( )
A、 B、 C、 D、6. 在数轴上,点A , B表示的数分别是 和2,则线段AB的中点表示的数是( )A、 B、 C、 D、7. 化简 的结果是( )A、 B、 C、 D、8. 如图,四边形ABCD和AECF都是菱形,点E , F在对角线BD上,∠ABC=60°,∠AEC=120°, ,则AB=( )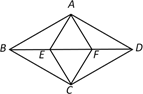 A、 B、 C、 D、9. 【材料阅读】
A、 B、 C、 D、9. 【材料阅读】材料1:从三张不同的卡片中选出两张排成一列,有6种不同的排法.抽象成数学问题,就是从3个不同的元素中选取2个元素的排列,排列数记为 .一般地,从n个不同的元素中选取m个元素的排列数记作 ,则: (m≤n).例:从5个不同的元素中选取3个元素排成一列的排列数为 .
材料2:从三张不同的卡片中选取两张,有3种不同的选法.抽象成数学问题就是从3个元素中选取2个元素的组合,组合数为 .一般地,从n个不同的元素中选取m个元素的组合数记作 ,则: .例:从6个不同的元素选3个元素的组合数为 .
【问题解决】
某单位要从9人中选取4人参加防护新冠疫情志愿服务活动,不同的选法共有( )
A、126种 B、63种 C、252种 D、21种10. 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A-45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为( ) A、 B、5 C、4 D、
A、 B、5 C、4 D、二、多选题
-
11. 甲、乙二人相约去科技创新大厦做核酸检测.下图表示的是他们在行走的过程中,离单位的距离y(单位:米)和行走的时间x(单位:分)间的关系.下列说法正确的是( )
 A、甲、乙二人第一次相遇,停留了10分钟 B、甲先到达目的地 C、甲停留10分钟之后提高了行走速度 D、甲行走的平均速度比乙行走的平均速度快12. 如图,在▱ABCD中,CD=2AD , BE⊥AD于点E , F为DC的中点,连结EF , BF.下列结论正确的是( )
A、甲、乙二人第一次相遇,停留了10分钟 B、甲先到达目的地 C、甲停留10分钟之后提高了行走速度 D、甲行走的平均速度比乙行走的平均速度快12. 如图,在▱ABCD中,CD=2AD , BE⊥AD于点E , F为DC的中点,连结EF , BF.下列结论正确的是( ) A、∠ABC=2∠ABF B、EF=BF C、S四边形DEBC=2S△EFB D、∠CFE=4∠DEF
A、∠ABC=2∠ABF B、EF=BF C、S四边形DEBC=2S△EFB D、∠CFE=4∠DEF三、填空题
-
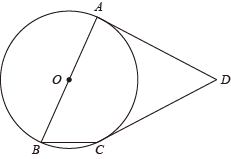
13. 计算: 的结果是 .14. 分解因式: .15. 已知方程 的一个根为 ,则另一根为 .16. 如图,AB是⊙O的直径,DA , DC与⊙O相切于点A , C.若AB=AD , 则∠ABC的正切值为.
 17. 如图,过原点的直线与反比例函数 的图象交于A , B两点,点A在第一象限,点C在x轴正半轴上,连结AC交反比例函数图象于点D . AE为∠BAC的平分线,过点B作AE的垂线,垂足为E , 连结DE , 若AC=3DC , △ADE的面积为6,则k的值为 .
17. 如图,过原点的直线与反比例函数 的图象交于A , B两点,点A在第一象限,点C在x轴正半轴上,连结AC交反比例函数图象于点D . AE为∠BAC的平分线,过点B作AE的垂线,垂足为E , 连结DE , 若AC=3DC , △ADE的面积为6,则k的值为 . 18. 如图,将正方形ABCD放置在平面直角坐标系中,点B为坐标原点,点C(4,0),A分别在x轴、y轴上,点E是BC边上一动点,将线段AE绕点E顺时针旋转90°,得到线段EP , Q是DE的中点,连接PQ,当PQ的长度取最小值时,BE的长度为.
18. 如图,将正方形ABCD放置在平面直角坐标系中,点B为坐标原点,点C(4,0),A分别在x轴、y轴上,点E是BC边上一动点,将线段AE绕点E顺时针旋转90°,得到线段EP , Q是DE的中点,连接PQ,当PQ的长度取最小值时,BE的长度为.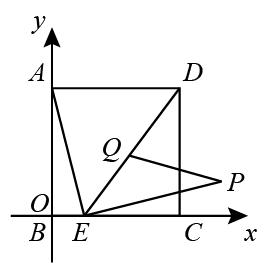
四、解答题
-
19. 解不等式组: .20. 2020年12月17日,中国研制的嫦娥五号返回器成功携带月球样品着陆地球,在接近大气层时,它的飞行速度接近第二宇宙速度,约为某列高铁全速行驶速度的112倍.如果以第二宇宙速度飞行560千米所用时间比该列高铁全速行驶10千米所用时间少50秒,那么第二宇宙速度是每秒多少千米?21. 某公司共有A , B , C三个部门,根据每个部门的员工人数和每人所创的年利润情况,绘制成如下的统计表和扇形图:
各部门人数及每人所创年利润统计表
部门
员工人数/人
每人所创的年利润/万元
A
5
10
B
b
8
C
c
5
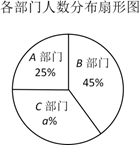
根据上述信息,解决下列问题:
(1)、在扇形图中,C部门所对应的圆心角的度数为;(2)、在统计表中,c的值为多少人;(3)、该公司员工所创的年利润的中位数是多少万元;(4)、已知A部门有2名男员工和3名女员工.公司要从A部门随机选取两名员工登台宣讲,请用画树状图或列表格的方法,求出恰好选取1名男员工和1名女员工的概率.22. 如图,在屋顶的斜坡面上安装太阳能热水器,先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,要求AD与水平线的夹角 为48°,且两支架之间的水平距离为150cm.现测量出屋顶斜面BC与水平面的夹角 为30°,支架AB的高度为20cm,求支架CD的高度.(结果精确到1cm,参考数值: , )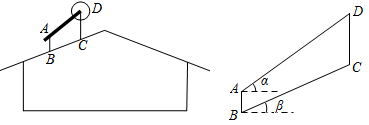 23. 如图,以AB为直径的⊙O , 分别交△ABC的边AC , BC于点D , E , 点D为 的中点.过点D作⊙O的切线,交BC于点F , 连接DE .
23. 如图,以AB为直径的⊙O , 分别交△ABC的边AC , BC于点D , E , 点D为 的中点.过点D作⊙O的切线,交BC于点F , 连接DE . (1)、求证:CF=EF;(2)、若AB=16,BE=6,求AD的长度.24. 已知抛物线 与x轴交于点A , B(A在B的左侧),抛物线的对称轴与x轴交于点D , 且OB=2OD.
(1)、求证:CF=EF;(2)、若AB=16,BE=6,求AD的长度.24. 已知抛物线 与x轴交于点A , B(A在B的左侧),抛物线的对称轴与x轴交于点D , 且OB=2OD. (1)、当 时,求抛物线的表达式;(2)、当抛物线 的对称轴在y轴的左侧时,存在垂直于x轴的直线,分别与直线 和抛物线 交于点P , Q , 且点P , Q均在x轴下方.请结合图象,求出b的取值范围.25. 在矩形ABCD中,AD= ,CD=3,点P是对角线AC上的一动点(不与点C , A重合),连接PB.
(1)、当 时,求抛物线的表达式;(2)、当抛物线 的对称轴在y轴的左侧时,存在垂直于x轴的直线,分别与直线 和抛物线 交于点P , Q , 且点P , Q均在x轴下方.请结合图象,求出b的取值范围.25. 在矩形ABCD中,AD= ,CD=3,点P是对角线AC上的一动点(不与点C , A重合),连接PB. (1)、如图Ⅰ,线段PB长度的最小值是;(2)、过点P作PF⊥PB , 交边AD所在的直线于点F , 连接BF , 如图Ⅱ,当点P运动到AC的中点时,BF与AC的交点为G , FP的中点为H , 求线段GH的长度;(3)、如图Ⅲ,将矩形ABCD放置在平面直角坐标系中,点A为坐标原点,点D , B分别在x轴、y轴上.当点P在运动的过程中:
(1)、如图Ⅰ,线段PB长度的最小值是;(2)、过点P作PF⊥PB , 交边AD所在的直线于点F , 连接BF , 如图Ⅱ,当点P运动到AC的中点时,BF与AC的交点为G , FP的中点为H , 求线段GH的长度;(3)、如图Ⅲ,将矩形ABCD放置在平面直角坐标系中,点A为坐标原点,点D , B分别在x轴、y轴上.当点P在运动的过程中:①∠FBP的大小是否发生变化?若不变,求出∠FBP的度数;若变化,说明理由;
②若△AFP是等腰三角形,求点F的坐标.