山东省泰安新泰市2022年(五四制)中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 的倒数是()A、 B、 C、2022 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为( )
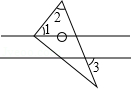 A、50° B、60° C、70° D、80°4. 截至2022年3月31日,全国累计报告接种新冠病毒疫苗327087.4万剂次,接种总人数达127770.9万,已完成全程接种124228.1万人.用科学记数法表示124228.1万为()A、 B、 C、 D、5. 如表是某超市上半年的月营业额 单位:万元 .
A、50° B、60° C、70° D、80°4. 截至2022年3月31日,全国累计报告接种新冠病毒疫苗327087.4万剂次,接种总人数达127770.9万,已完成全程接种124228.1万人.用科学记数法表示124228.1万为()A、 B、 C、 D、5. 如表是某超市上半年的月营业额 单位:万元 .月营业额
月数
下列结论错误的是()
A、平均数是 B、中位数 C、众数是 D、方差是6. 如图是由4个相同的小正方体成的物体,将它在水平面内顺时针旋转90°后,其主视图是( )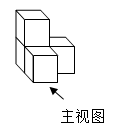 A、
A、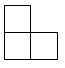 B、
B、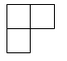 C、
C、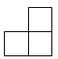 D、
D、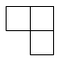 7. 关于x的方程 有实数根,则k的取值范围是 ( )A、 且 B、 且 C、 D、8. 如图, 是 的直径,C,D是 上的点, ,过点C作 的切线交 的延长线于点E,若 ,则 的半径为( )
7. 关于x的方程 有实数根,则k的取值范围是 ( )A、 且 B、 且 C、 D、8. 如图, 是 的直径,C,D是 上的点, ,过点C作 的切线交 的延长线于点E,若 ,则 的半径为( ) A、 B、 C、 D、9. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、10. 如图, 是 的直径, , 是 上的两点,且 平分 , 分别与 , 相交于点 , ,则下列结论不一定成立的是( )
A、 B、 C、 D、9. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、10. 如图, 是 的直径, , 是 上的两点,且 平分 , 分别与 , 相交于点 , ,则下列结论不一定成立的是( )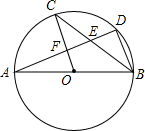 A、 B、 C、 D、11. 如图, 为正方形 对角线 上一动点, , , 在 上结论:① ;② ;③ ;④若 , ,则 .其中正确结论的个数是 ( )
A、 B、 C、 D、11. 如图, 为正方形 对角线 上一动点, , , 在 上结论:① ;② ;③ ;④若 , ,则 .其中正确结论的个数是 ( )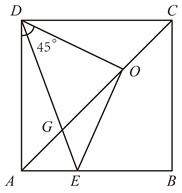 A、1 B、2 C、3 D、412. 在平面直角坐标系中,点A、B在x轴上,点C在y轴上, 是等边三角形,P是 边上动点,连接 ,以 为边在 的右侧作等边三角形 ,连接 . 的面积为 , 的中点为M,当点P在 边上运动时,线段 的最小值为()
A、1 B、2 C、3 D、412. 在平面直角坐标系中,点A、B在x轴上,点C在y轴上, 是等边三角形,P是 边上动点,连接 ,以 为边在 的右侧作等边三角形 ,连接 . 的面积为 , 的中点为M,当点P在 边上运动时,线段 的最小值为() A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题
-
13. 已知x、y满足方程组 ,则x﹣y的值为14. 小超在周末利用无人机测量滨湖广场上风帆的高度.如图所示,无人机在距离地面 米的P处测得A处的俯角为 ,B处的俯角为 ,若斜面 的坡度为 ,则风帆的高 是米.
 15. 如图,在菱形中,点E是的中点,以C为圆心,为半径作弧,交于点F,连接、若 , , 则阴影部分的面积为 .
15. 如图,在菱形中,点E是的中点,以C为圆心,为半径作弧,交于点F,连接、若 , , 则阴影部分的面积为 . 16. 如图,已知抛物线 与x轴相交于于点A,B,与y轴的交于点C.点 在平面直角坐标系第一象限内的抛物线上运动,设 的面积为S.下列结论:① ;② ;③ ,其中,正确结论的序号是 . (所有正确的序号都填上)
16. 如图,已知抛物线 与x轴相交于于点A,B,与y轴的交于点C.点 在平面直角坐标系第一象限内的抛物线上运动,设 的面积为S.下列结论:① ;② ;③ ,其中,正确结论的序号是 . (所有正确的序号都填上) 17. 如图,在 纸片中, , , ,点D,E分别在 , 上,连结 ,将 沿 翻折,使点A的对应点F落在 的延长线上,若 平分 ,则 的长为 .
17. 如图,在 纸片中, , , ,点D,E分别在 , 上,连结 ,将 沿 翻折,使点A的对应点F落在 的延长线上,若 平分 ,则 的长为 . 18. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和 的展开式的各项系数,此三角形称为“杨辉三角”,据“杨辉三角”,设 的展开式中第三项的系数为m, 的展开式中第三项的系数n,则 .
18. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和 的展开式的各项系数,此三角形称为“杨辉三角”,据“杨辉三角”,设 的展开式中第三项的系数为m, 的展开式中第三项的系数n,则 .………………………….1
………………………..1 1
……………………1 2 1
……………………1 3 3 1
……………………1 4 6 4 1
……
三、解答题
-
19.(1)、解不等式组: ,并写出它的所有整数解;(2)、先化简,再求值: ,其中 .20. 3月5日是学雷锋纪念日,为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,新泰市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
 (1)、求该班的人数;(2)、请把折线统计图补充完整:(3)、求扇形统计图中,网络文明部分对应的圆心角的度数;(4)、该校计划对参加活动最积极的小颖同学奖励两枚“2022·北京冬梦之约”的邮票.现有如图所示“2022·北京冬梦之约”的四枚邮票供小颖选择,依次记为A,B,C,D,背面完全相同.将这四枚邮票背面朝上,洗匀放好,小颖从中随机抽取一枚不放回,再从中随机抽取一枚.请用列表或画树状图的方法,求小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率.
(1)、求该班的人数;(2)、请把折线统计图补充完整:(3)、求扇形统计图中,网络文明部分对应的圆心角的度数;(4)、该校计划对参加活动最积极的小颖同学奖励两枚“2022·北京冬梦之约”的邮票.现有如图所示“2022·北京冬梦之约”的四枚邮票供小颖选择,依次记为A,B,C,D,背面完全相同.将这四枚邮票背面朝上,洗匀放好,小颖从中随机抽取一枚不放回,再从中随机抽取一枚.请用列表或画树状图的方法,求小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率. 21. 如图,已知一次函数 与反比例函数 的图象交于第一象限内的点 和 ,与x轴交于点C,交y轴于点D.
21. 如图,已知一次函数 与反比例函数 的图象交于第一象限内的点 和 ,与x轴交于点C,交y轴于点D.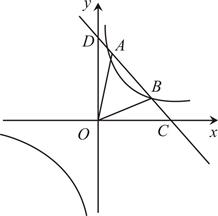 (1)、分别求出这两个函数的表达式;(2)、连接 、 ,求 的面积;(3)、点P为坐标平面内的点,若点O,A,C,P组成的四边形是平行四边形,请直接写出点P的坐标.22. 2022年4月8日,CCTV-13新闻频道《朝闻天下》,报道了山东新泰《香椿进入收获期“椿”意盎然助增收》,我市香椿将销往全国各地.某商店决定购进一批香椿,已知甲种香椿每件的进价比乙种香椿每件的进价少6元,花180元购买甲种香椿的件数与花240元购买乙种香椿的件数相等.(1)、求甲、乙两种香椿每件的进价;(2)、由于畅销,第一批购进的香椿已经售馨,现该商店决定用4320元再购进一批甲、乙两种香椿共200件.结果恰逢批发商进行调价,甲种香椿在第一批进价的基础上9折销售,而乙种香椿比第一批进价提高了5%,则最多可购买乙种香椿多少件?23. 在 中, , , 于点D.
(1)、分别求出这两个函数的表达式;(2)、连接 、 ,求 的面积;(3)、点P为坐标平面内的点,若点O,A,C,P组成的四边形是平行四边形,请直接写出点P的坐标.22. 2022年4月8日,CCTV-13新闻频道《朝闻天下》,报道了山东新泰《香椿进入收获期“椿”意盎然助增收》,我市香椿将销往全国各地.某商店决定购进一批香椿,已知甲种香椿每件的进价比乙种香椿每件的进价少6元,花180元购买甲种香椿的件数与花240元购买乙种香椿的件数相等.(1)、求甲、乙两种香椿每件的进价;(2)、由于畅销,第一批购进的香椿已经售馨,现该商店决定用4320元再购进一批甲、乙两种香椿共200件.结果恰逢批发商进行调价,甲种香椿在第一批进价的基础上9折销售,而乙种香椿比第一批进价提高了5%,则最多可购买乙种香椿多少件?23. 在 中, , , 于点D. (1)、如图1,点E,F分别在 , 上,且 ,求证: ;(2)、如图2,点M在 的延长线上,点N在 上,且 ,求证: .24.
(1)、如图1,点E,F分别在 , 上,且 ,求证: ;(2)、如图2,点M在 的延长线上,点N在 上,且 ,求证: .24. (1)、问题背景:如图1, , , , 求证: ;(2)、尝试应用:如图2,E为正方形 外一点, ,过点D作 ,垂足为F,连接 .若 ,求 的值;(3)、拓展创新:如图3,四边形 是正方形,点F是线段 上一点,以 为对角线作正方形 ,连接 , .当 , 时,求 的长.25. 如图1,已知抛物线 与x轴交于 、 两点,与y轴交于点C,顶点为点D.
(1)、问题背景:如图1, , , , 求证: ;(2)、尝试应用:如图2,E为正方形 外一点, ,过点D作 ,垂足为F,连接 .若 ,求 的值;(3)、拓展创新:如图3,四边形 是正方形,点F是线段 上一点,以 为对角线作正方形 ,连接 , .当 , 时,求 的长.25. 如图1,已知抛物线 与x轴交于 、 两点,与y轴交于点C,顶点为点D. (1)、求该抛物线的函数表达式;(2)、点F为第一象限内抛物线上一点,连接 交y轴于点M,设点F的横坐标为t,线段 的长为d,求d与t之间的函数关系式.(3)、点E是点D关于x轴的对称点,经过点A的直线 与该抛物线交于点F,点P是直线 上的一个动点,连接 、 、 ,记 的面积为 , 的面积为 ,求 的值.
(1)、求该抛物线的函数表达式;(2)、点F为第一象限内抛物线上一点,连接 交y轴于点M,设点F的横坐标为t,线段 的长为d,求d与t之间的函数关系式.(3)、点E是点D关于x轴的对称点,经过点A的直线 与该抛物线交于点F,点P是直线 上的一个动点,连接 、 、 ,记 的面积为 , 的面积为 ,求 的值.