山东省泰安市宁阳县2022年（五四制）中考一模数学试题

试卷更新日期：2022-05-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 三个等圆按如图所示的方式摆放，若再添加一个等圆，使所得图形是中心对称图形，则这个等圆的位置可以是（）

A、 B、 C、 D、

查看试题解析
2. 某高校计划派出甲、乙、丙3名男生和A、B、C3名女生共6名志愿者参与北京冬奥会工作，现在将他们分配到北京、延庆2个赛区进行培训，其中1名男性志愿者和1名女性志愿者去北京赛区，其他都去延庆赛区，则甲和A恰好被选去北京赛区培训的概率为（）

A、 $\frac{1}{20}$ B、 $\frac{1}{16}$ C、 $\frac{1}{9}$ D、 $\frac{1}{8}$

查看试题解析
3. 如图， $Rt Δ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，交 $B C$ 于点D， $A B = 10$ ， $S_{Δ A B D} = 15$ ，则 $C D$ 的长为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 当 $0 \leq x \leq m$ 时，函数 $y = - x^{2} + 4 x - 3$ 的最小值为-3，最大值为1，则m的取值范围是（）

A、 $- 1 \leq m \leq 0$ B、 $2 \leq m < \frac{7}{2}$ C、 $2 \leq m \leq 4$ D、 $\frac{9}{4} < m \leq \frac{7}{2}$

查看试题解析
5. 如图，点A、B、C是⊙O上的三点，且四边形ABCO是平行四边形，OF⊥OC交圆O于点F，则∠BAF等于(　　)

A、12.5° B、15° C、20° D、22.5°

查看试题解析
6. 某校交响乐团有90名成员，下表是合唱团成员的年龄分布统计表：对于不同的x ，下列关于年龄的统计量不会发生改变的是（　　）

年龄（单位：岁）

13

14

15

16

17

频数（单位：名）

17

29

x

26﹣x

18

A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差

查看试题解析
7. 如图，在 $⊙ O$ 中，CD为 $⊙ O$ 的直径， $C D ⊥ A B$ ， $∠ A E C = 60 °$ ， $O B = 4$ ，则弦 $A B =$ （）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $4 \sqrt{2}$ D、 $4 \sqrt{3}$

查看试题解析
8. 如图，在平面直角坐标系中，一次函数 $y = \frac{4}{3} x + 4$ 的图象与x轴、y轴分别相交于点B、点A，以线段AB为边作正方形ABCD，且点C在反比例函数 $y = \frac{k}{x} (x < 0)$ 图象上，则k的值为（）

A、21 B、－42 C、42 D、－21

查看试题解析
9. 如图，在 $△ A B C$ 中，D在AC边上，AD：DC=1：2，O是BD的中点，连接AO并延长交BC于E ，若BE=1，则EC=（）

A、 $\frac{3}{2}$ B、2 C、3 D、4

查看试题解析
10. 如图，抛物线 $L_{1} ： y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴只有一个公共点A（1，0），与 $y$ 轴交于点B（0，2），虚线为其对称轴，若将抛物线向下平移两个单位长度得抛物线 $L_{2}$ ，则图中两个阴影部分的面积和为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 如图，边长为4的正方形ABCD的对角线AC与BD交于点O ，将正方形ABCD沿直线DF折叠，点C落在对角线BD上的点E处，折痕DF交AC于点M ，则OM长是（　　）

A、 $2 \sqrt{2}$ B、 $4 - 2 \sqrt{2}$ C、 $4 - \sqrt{2}$ D、2﹣ $\sqrt{2}$

查看试题解析
12. 如图，直线y＝x+6分别与x轴、y轴相交于点M ， N ， ∠MPN＝90°，点C(0，3)，则PC长度的最小值是（　　）

A、3 $\sqrt{2} -$ 3 B、3﹣2 $\sqrt{2}$ C、 $\frac{2 \sqrt{5}}{5}$ D、3

查看试题解析

二、填空题

13. 小丽的笔试成绩为100分，面试成绩为90分，若笔试成绩、面试成绩按6：4计算平均成绩，则小丽的平均成绩是分.

查看试题解析
14. 如图，将三个相同的三角尺（内角分别为30°，60°，90°）的一个顶点重合放置，如果 $∠ 1 = 22 °$ ， $∠ 2 = 26 °$ ，那么 $∠ 3$ 的度数是．

查看试题解析
15. 如图，大、小两个正方形的中心均与平面直角坐标系的原点O重合，边分别与坐标轴平行，反比例函数 $y = \frac{k}{x}$ 的图象与大正方形的一边交于点 $A (2 ， 4)$ ，且经过小正方形的顶点B．则图中阴影部分的面积为．

查看试题解析
16. 当x满足 ${\begin{array}{l} 2 x < 4 x - 4 \\ \frac{1}{3} (x - 6) > \frac{1}{2} (x - 6) \end{array}$ 时，方程 $x^{2} - 2 x - 5 = 0$ 的根是．

查看试题解析
17. 如图，在平面直角坐标系中，等腰直角三角形 $O A A_{1}$ 的直角边 $O A$ 在 $x$ 轴上，点 $A_{1}$ 在第一象限，且 $O A = 1$ ，以点 $A_{1}$ 为直角顶点， $O A_{1}$ 为一直角边作等腰直角三角形 $O A_{1} A_{2}$ ，再以点 $A_{2}$ 为直角顶点， $O A_{2}$ 为直角边作等腰直角三角形 $O A_{2} A_{3} \dots$ 依此规律，则点 $A_{2021}$ 的坐标是.

查看试题解析
18. 二次函数y=ax²+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论：
①ac＜0；
②当x＞1时，y的值随x值的增大而减小．
③3是方程ax²+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax²+（b﹣1）x+c＞0．
其中正确的结论是．

查看试题解析

三、解答题

19. 化简：

(1)、 $(1 + \frac{2}{x - 1}) \div \frac{x + 1}{x^{2} - 2 x + 1}$ ．

(2)、 $\sqrt{3} (\sqrt{2} - \sqrt{3}) - \sqrt{24} - | \sqrt{6} - 3 |$ ．

查看试题解析
20. 如图，已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 与正比例函数 $y = 2 x$ 的图象交于 $A (1 ， m)$ ， $B$ 两点.

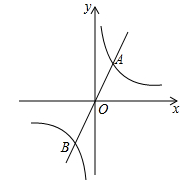(1)、求该反比例函数的表达式；

(2)、若点 $C$ 在 $x$ 轴上，且 $△ B O C$ 的面积为3，求点 $C$ 的坐标.

查看试题解析
21. 如图①，在平行四边形 $A B C D$ 中，将对角线 $A C$ 分别向两端延长到点E和F，使得 $A E = C F$ ，连接 $D F$ ， $B E$ ．

(1)、求证： $Δ C D F ≌ Δ A B E$ ；

(2)、如图②，连接 $D E$ ， $B D$ ， $B F$ ，若 $A C ⊥ B D$ ，四边形 $B E D F$ 是何种特殊四边形？

查看试题解析
22. 已知正方形ABCD ， E ， F为平面内两点．

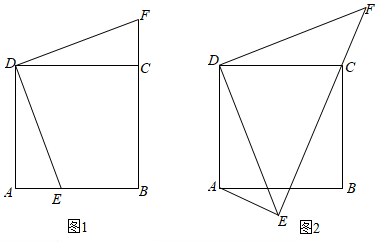(1)、（探究建模）
如图1，当点E在边AB上时， $D E ⊥ D F$ ，且B ， C ， F三点共线，求证： $A E = C F$ ；

(2)、（类比应用）
如图2，当点E在正方形ABCD外部时， $D E ⊥ D F$ ， $A E ⊥ E F$ ，且E ， C ， F三点共线．猜想并证明线段AE ， CE ， DE之间的数量关系；

查看试题解析
23. 随着龙虾节的火热举办，某龙虾养殖大户为了发挥技术优势，一次性收购了10000kg小龙虾，计划养殖一段时间后再出售．已知每天养殖龙虾的成本相同，放养10天的总成本为166000，放养30天的总成本为178000元．设这批小龙虾放养t天后的质量为akg，销售单价为y元/kg，根据往年的行情预测，a与t的函数关系为a= ${\begin{matrix} \end{matrix} \begin{matrix} 10000 (0 \leq t \leq 20) \\ 100 t + 8000 (20 < t \leq 50) \end{matrix}$ ，y与t的函数关系如图所示．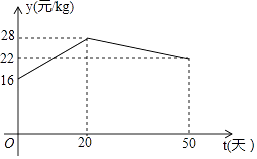

(1)、设每天的养殖成本为m元，收购成本为n元，求m与n的值；

(2)、求y与t的函数关系式；

(3)、如果将这批小龙虾放养t天后一次性出售所得利润为W元．问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大？最大利润是多少？
（总成本=放养总费用+收购成本；利润=销售总额﹣总成本）

查看试题解析
24. 如图，△ABC是 $⊙ O$ 的内接三角形，过点C作 $⊙ O$ 的切线交BA的延长线于点F，AE是 $⊙ O$ 的直径，连接E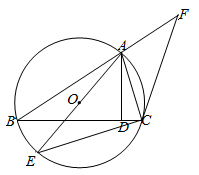C

(1)、求证： $∠ ACF = ∠ B$ ；

(2)、若AB=BC，AD⊥BC于点D，FC=4，FA=2，求AD·AE的值

查看试题解析
25. 已知抛物线 $y = a x^{2} + 2 a x - 3 a$ （a为常数， $a \neq 0$ ）

(1)、求该抛物线的对称轴和顶点坐标（用含a的代数式表示）；

(2)、若 $a < 0$ ．且 $P (m ， y_{1})$ 与 $Q (- 5 ， y_{2})$ 是该抛物线上的两点，且 $y_{1} < y_{2}$ ，求m的取值范围；

(3)、如图，当 $a = - 1$ 时，设该抛物线与x轴分别交于A、B两点，点A在点B的左侧，与y轴交于点C．点D是直线 $A C$ 上方抛物线上的一个动点， $B D$ 交 $A C$ 于点E，设点D的横坐标为t，记 $S = \frac{S_{Δ A D E}}{S_{Δ A B E}}$ ，当t为何值时，S取得最大值？并求出S的最大值.

查看试题解析

年龄（单位：岁）	13	14	15	16	17
频数（单位：名）	17	29	x	26﹣x	18

x	﹣1	0	1	3
y	﹣1	3	5	3