山东省泰安市岱岳区、高新区2022年中考第一轮模拟数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. -3的相反数是( )A、-3 B、3 C、±3 D、2. 下列运算中,正确的是( )A、a6÷a3=a2 B、2-2=﹣4 C、 D、3a+2a2=5a23. 如图,AB∥CD , AF交CD于点E , 且BE⊥AF , ∠AEC=40°,则∠B为( )°.
 A、40 B、50 C、130 D、1404. 实验中学选择10名青少年志愿者参加读书日活动,年龄如表所示:这10名志愿者年龄的众数和中位数分别是( )
A、40 B、50 C、130 D、1404. 实验中学选择10名青少年志愿者参加读书日活动,年龄如表所示:这10名志愿者年龄的众数和中位数分别是( )年龄
12
13
14
15
人数
2
3
4
1
A、14,13 B、14,14 C、14,13.5 D、13,145. 华为某型号手机经过2次降价后的价格是2次降价前价格的 ,则每次降价的平均百分比是()A、10% B、20% C、15% D、25%6. 如图,AB是⊙O的直径,D为⊙O上一点,过 上一点T作⊙O的切线TC , 且TC⊥AD于点C . 若∠DAB=58°,求∠ATC的度数是( ) A、51° B、58° C、61° D、58°7. 图1是2002年世界数学大会(ICM)的会徽,其主体图案(如图2)是由四个全等的直角三角形组成的四边形.若 ,AB=1,则CD的长为( )
A、51° B、58° C、61° D、58°7. 图1是2002年世界数学大会(ICM)的会徽,其主体图案(如图2)是由四个全等的直角三角形组成的四边形.若 ,AB=1,则CD的长为( )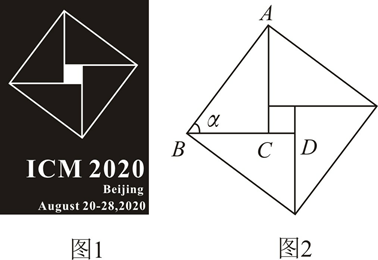 A、 B、 C、 D、8. 若关于x的不等式4x+m≥0有且仅有两个负整数解,则m的取值范围是( )A、8<m≤12 B、8<m<12 C、8<m≤12 D、8≤m<129. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、10. 如图,点C , D在以AB为直径的⊙O上,且CD平分∠ACB , 若CD=4 ,∠CAB=75°,则AB的长是( )
A、 B、 C、 D、8. 若关于x的不等式4x+m≥0有且仅有两个负整数解,则m的取值范围是( )A、8<m≤12 B、8<m<12 C、8<m≤12 D、8≤m<129. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、10. 如图,点C , D在以AB为直径的⊙O上,且CD平分∠ACB , 若CD=4 ,∠CAB=75°,则AB的长是( )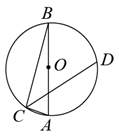 A、8 B、4 C、8 D、411. 如图,在 中, 为斜边 的中线,过点D作 于点E , 延长 至点F , 使 ,连接 ,点G在线段 上,连接 ,且 .下列结论:① ;②四边形 是平行四边形;③ ;④ .其中正确论的个数是( )
A、8 B、4 C、8 D、411. 如图,在 中, 为斜边 的中线,过点D作 于点E , 延长 至点F , 使 ,连接 ,点G在线段 上,连接 ,且 .下列结论:① ;②四边形 是平行四边形;③ ;④ .其中正确论的个数是( )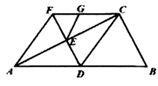 A、1个 B、2个 C、3个 D、4个12. 如图,A点坐标(0,4),B为x轴上一动点,将线段AB绕点B顺时针旋转90°,得到BC , 连接OC , 则B在运动过程中,线段OC的最小值是( )
A、1个 B、2个 C、3个 D、4个12. 如图,A点坐标(0,4),B为x轴上一动点,将线段AB绕点B顺时针旋转90°,得到BC , 连接OC , 则B在运动过程中,线段OC的最小值是( )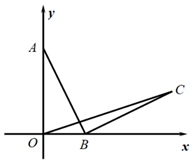 A、4 B、4 C、2 D、2
A、4 B、4 C、2 D、2二、填空题
-
13. 第24届奥林匹克冬季运动会于2022年2月4号至20号在北京举行,在中国已经有3亿人参与了冰雪运动.根据预测,中国冬季运动的市场价值在2025年将会达到1500亿美元,这也会给全世界的冬季运动带来巨大的推动作用.1500亿美元用科学记数法表示是美元.14. 计算(π﹣3)0﹣| 3|﹣2cos30°= .15. 如图, ABC内接于⊙O , ∠B=60°,点E在直径CD的延长线上,AE切⊙O于点A , 且AE=AC , AC=6,阴影部分的面积是 .
 16. 如图,反比例函数y (k>0)的图象与直线AB交于点A(2,4),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC , 交反比例函数的图象于点C , 在平面内存在点D , 使得以A , B , C , D四点为顶点的四边形为平行四边形,则点D的坐标是 .
16. 如图,反比例函数y (k>0)的图象与直线AB交于点A(2,4),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC , 交反比例函数的图象于点C , 在平面内存在点D , 使得以A , B , C , D四点为顶点的四边形为平行四边形,则点D的坐标是 .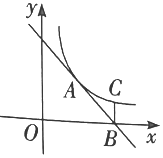 17. 如图,在四边形ABCD中,AB⊥BC , AD⊥AC , AD=AC , ∠BAD=105°,点E和点F分别是AC和CD的中点,连接BE , EF , BF , 若CD=8,则 BEF的面积是 .
17. 如图,在四边形ABCD中,AB⊥BC , AD⊥AC , AD=AC , ∠BAD=105°,点E和点F分别是AC和CD的中点,连接BE , EF , BF , 若CD=8,则 BEF的面积是 .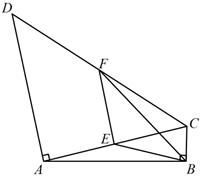 18. 如图, 中, , ,BC边上的高 ,点P1、Q1、H1分别在边AD、AC、CD上,且四边形P1Q1H1D为正方形,点P2、Q2、H2分别在边Q1H1、CQ1、CH1上,且四边形P2Q2H2H1为正方形,…按此规律操作下去,则线段CQ2022的长度为 .
18. 如图, 中, , ,BC边上的高 ,点P1、Q1、H1分别在边AD、AC、CD上,且四边形P1Q1H1D为正方形,点P2、Q2、H2分别在边Q1H1、CQ1、CH1上,且四边形P2Q2H2H1为正方形,…按此规律操作下去,则线段CQ2022的长度为 .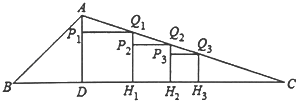
三、解答题
-
19. 先化简,再求值: ,其中x的值从不等式组 的整数解中选取.20. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
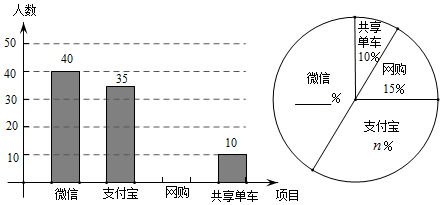 (1)、根据图中信息求出m= , n=;(2)、请你帮助他们将这两个统计图补全;(3)、根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?(4)、已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.21. 如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y= (x>0)的图象经过点B.
(1)、根据图中信息求出m= , n=;(2)、请你帮助他们将这两个统计图补全;(3)、根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?(4)、已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.21. 如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y= (x>0)的图象经过点B.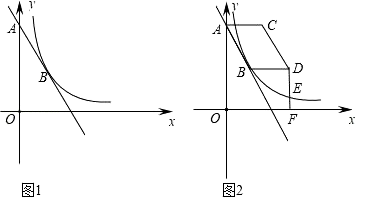 (1)、求a和k的值;(2)、将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.
(1)、求a和k的值;(2)、将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.①如图2,当m=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,求E点的坐标;
②在线段AB运动过程中,连接BC,若△BCD是等腰三形,求所有满足条件的m的值.
22. 北京冬奥会、冬残奥会期间,大批的大学生志愿者参与服务工作,为双奥的成功举办做出巨大贡献.同时,“绿色办奥”是北京冬奥会、冬残奥会四大办奥理念之一.期间,节能与清洁能源车辆占全部赛事保障车辆的84.9%,为历届冬奥会最高.冬奥会开幕式当天,北京大学组织本校全体参与开幕式活动的志愿者统一乘车去国家体育场鸟巢,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)、计划调配36座新能源客车多少辆?北京大学共有多少名志愿者?(2)、若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?23. 如图,将矩形ABCD绕着点B逆时针旋转得到矩形GBEF , 使点C恰好落到线段AD上的E点处,连接CE , 连接CG交BE于点H .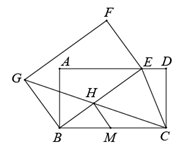 (1)、求证:CE平分∠BED;(2)、取BC的中点M , 连接MH , 求证:MH BG;(3)、若BC=2AB=4,求CG的长.24. 如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),二次函数y=x2+bx﹣2的图象经过C点.
(1)、求证:CE平分∠BED;(2)、取BC的中点M , 连接MH , 求证:MH BG;(3)、若BC=2AB=4,求CG的长.24. 如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),二次函数y=x2+bx﹣2的图象经过C点.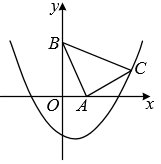 (1)、求二次函数的解析式;(2)、若点P是抛物线的一个动点且在x轴的下方,则当点P运动至何处时,恰好使△PBC的面积等于△ABC的面积的两倍.(3)、若点Q是抛物线上的一个动点,则当点Q运动至何处时,恰好使∠QAC=45°?请你求出此时的Q点坐标.25. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E , 交BA的延长线于点F .
(1)、求二次函数的解析式;(2)、若点P是抛物线的一个动点且在x轴的下方,则当点P运动至何处时,恰好使△PBC的面积等于△ABC的面积的两倍.(3)、若点Q是抛物线上的一个动点,则当点Q运动至何处时,恰好使∠QAC=45°?请你求出此时的Q点坐标.25. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E , 交BA的延长线于点F .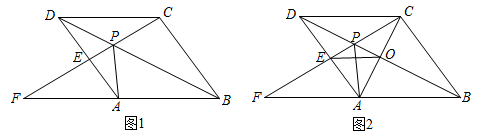 (1)、求证:PE•PF= .(2)、如图2,连接AC交BD于O , 连接OE , 若CE⊥BC , 求证: POC∽ AEC .(3)、PE ,OE ,求EF的长及菱形的边长.
(1)、求证:PE•PF= .(2)、如图2,连接AC交BD于O , 连接OE , 若CE⊥BC , 求证: POC∽ AEC .(3)、PE ,OE ,求EF的长及菱形的边长.