北京市燕山区2022 年初中毕业年级质量监测(一)数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 下图是某几何体的三视图,该几何体是()
 A、圆锥 B、圆柱 C、三棱锥 D、长方体2. 小云同学在“百度”搜索引擎中输入“北京2022冬奥会”,能找到相关结果约为42500000个,将42500000用科学记数法表示应为()A、 B、 C、 D、3. 如图,直线 , 交于点O . 射线 平分 ,若 ,则 等于( )
A、圆锥 B、圆柱 C、三棱锥 D、长方体2. 小云同学在“百度”搜索引擎中输入“北京2022冬奥会”,能找到相关结果约为42500000个,将42500000用科学记数法表示应为()A、 B、 C、 D、3. 如图,直线 , 交于点O . 射线 平分 ,若 ,则 等于( ) A、 B、 C、 D、4. 下列图形中,既是中心对称图形也是轴对称图形的是()A、
A、 B、 C、 D、4. 下列图形中,既是中心对称图形也是轴对称图形的是()A、 B、
B、 C、
C、 D、
D、 5. 实数a , b , c , d在数轴上的对应点的位置如图所示,则正确的结论是( )
5. 实数a , b , c , d在数轴上的对应点的位置如图所示,则正确的结论是( ) A、 B、 C、 D、6. 如图,有5张形状、大小、质地均相同的卡片,正面分别印有北京冬奥会的会徽、吉祥物(冰墩墩)、主题口号和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是奖牌的概率是( )
A、 B、 C、 D、6. 如图,有5张形状、大小、质地均相同的卡片,正面分别印有北京冬奥会的会徽、吉祥物(冰墩墩)、主题口号和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是奖牌的概率是( ) A、 B、 C、 D、7. 已知 , , , .若n为整数且 ,则n的值为( )A、43 B、44 C、45 D、468. 线段 .动点以每秒1个单位长度的速度从点出发,沿线段 运动至点B,以线段 为边作正方形 ,线段 长为半径作圆.设点的运动时间为t , 正方形 周长为y , 的面积为S,则y与t , S与t满足的函数关系分别是()
A、 B、 C、 D、7. 已知 , , , .若n为整数且 ,则n的值为( )A、43 B、44 C、45 D、468. 线段 .动点以每秒1个单位长度的速度从点出发,沿线段 运动至点B,以线段 为边作正方形 ,线段 长为半径作圆.设点的运动时间为t , 正方形 周长为y , 的面积为S,则y与t , S与t满足的函数关系分别是() A、正比例函数关系,一次函数关系 B、一次函数关系,正比例函数关系 C、正比例函数关系,二次函数关系 D、反比例函数关系,二次函数关系
A、正比例函数关系,一次函数关系 B、一次函数关系,正比例函数关系 C、正比例函数关系,二次函数关系 D、反比例函数关系,二次函数关系二、填空题
-
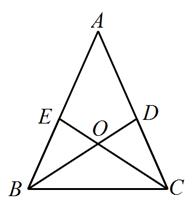
9. 若代数式 有意义,则实数x的取值范围是 .10. 分解因式: = .11. 写出一个比 大且比 小的整数是 .12. 方程组 的解为13. 在直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的横坐标分别为 , ,则 的值为 .14. 如图,在 中,点D、E分别 、 上的点, 与 交于点O . 给出下列三个条件:① ;② ;③ .利用其中两个条件可以证明 是等腰三角形,这两个条件可以是 .
 15. 是平面直角坐标系中的两点,线段 长度的最小值为 .16. 甲、乙、丙三人进行羽毛球比赛赛前训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现甲共当裁判9局,乙、丙分别进行了14局、12局比赛,在这半天的训练中,甲、乙、丙三人共进行了局比赛,其中最后一局比赛的裁判是 .
15. 是平面直角坐标系中的两点,线段 长度的最小值为 .16. 甲、乙、丙三人进行羽毛球比赛赛前训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现甲共当裁判9局,乙、丙分别进行了14局、12局比赛,在这半天的训练中,甲、乙、丙三人共进行了局比赛,其中最后一局比赛的裁判是 .三、解答题
-
17. 计算:18. 疫情防控过程中,很多志愿者走进社区参加活动.如图所示,小冬老师从A处出发,要到A地北偏东 方向的C处,他先沿正东方向走了 到达B处,再沿北偏东 方向走,恰能到达目的地C处,求A , C两地的距离.(结果取整数,参考数据: )
 19. 已知:如图,直线l , 和直线外一点P .
19. 已知:如图,直线l , 和直线外一点P .求作:过点P作直线PC , 使得PC∥l ,
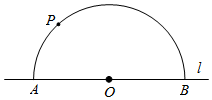
作法:①在直线l上取点O , 以点O为圆心,OP长为半径画圆,交直线l于A , B两点;
②连接AP , 以点B为圆心,AP长为半径画弧,交半圆于点C;
③作直线PC .
直线PC即为所求作.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明:证明:连接BP .
∵BC=AP ,
∴ ▲ .
∴∠ABP=∠BPC( )(填推理依据).
∴直线PC∥直线l .
20. 已知关于x的方程 总有两个不相等的实数根.(1)、求k的取值范围;(2)、写出一个k的值,并求此时方程的根.21. 如图,在菱形 中,对角线 与 相交于点O , 过点D作 交 的延长线于点E . (1)、求证:四边形 是平行四边形;(2)、若 , ,求 的值.22. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向上平移3个单位长度得到.(1)、求这个一次函数的解析式;(2)、当 时,对于x的每一个值,函数 的值大于一次函数 的值,直接写出m的取值范围.23. 农业农村经济在国民经济中占有重要地位,科技兴农、为促进乡村产业振兴提供有力支撑.为了解甲、乙两种新品猕猴桃的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.
(1)、求证:四边形 是平行四边形;(2)、若 , ,求 的值.22. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向上平移3个单位长度得到.(1)、求这个一次函数的解析式;(2)、当 时,对于x的每一个值,函数 的值大于一次函数 的值,直接写出m的取值范围.23. 农业农村经济在国民经济中占有重要地位,科技兴农、为促进乡村产业振兴提供有力支撑.为了解甲、乙两种新品猕猴桃的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.a . 测评分数(百分制)如下:
甲77 79 80 80 85 86 86 87 88 89 89 90 91
91 91 91 91 92 93 95 95 96 97 98 98
乙69 87 79 79 86 79 87 89 90 89 90 90 90
91 90 92 92 94 92 95 96 96 97 98 98
b . 按如下分组整理、描述这两组样本数据:
甲
0
a
9
14
乙
1
3
b
16
注:分数90分及以上为优秀,80~89分为合格,80分以下为不合格.
c . 甲、乙两种猕猴桃测评分数的平均数、众数、中位数如下表所示:
品种
平均数
众数
中位数
甲
89.4
91
d
乙
89.4
c
90
根据以上信息,回答下列问题:
(1)、写出表中a , b , c , d的值;(2)、记甲种猕猴桃测评分数的方差为 ,乙种猕猴桃测评分数的方差为 ,则 , 的大小关系为;(3)、根据抽样调查情况,可以推断种猕猴桃的质量较好,理由为 . (至少从两个不同的角度说明推断的合理性)24. 某景观公园内人工湖里有一组小型喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在湖面上距水枪水平距离为d米的位置,水柱距离湖面高度为h米.d(米)
0.5
1.0
2.0
3.0
3.5
4.5
…
h(米)
1.6
2.1
2.5
2.1
m
0
…

请解决以下问题:
(1)、以水枪与湖面交点为原点,原点与水柱落地处所在直线为x轴,水枪所在直线为y轴,在下边网格中建立平面直角坐标系,根据已知数据描点,并用平滑的曲线连接.(2)、请结合表中所给数据或所画图象,写出水柱最高点的坐标.(3)、湖面上距水枪水平距离为3.5米时,水柱距离湖面的高度m=米.(4)、现公园想通过喷泉设立新的游玩项目,准备通过调节水枪高度,使得公园湖中的游船能从喷泉下方通过.游船左右两边缘最宽处有一个长方体形状的遮阳棚,若游船宽(指船的最大宽度)为2米,从水面到棚顶的高度为2.1米,要求是游船从喷泉水柱中间通过时,为避免游船被喷泉淋到,顶棚到水柱的垂直距离均不小于0.5米.请问公园该如何调节水枪高度以符合要求?请通过计算说明理由.25. 如图, 为 的直径,点C在 上,过点C作 的切线 ,过点A作 于点D , 交 的延长线于点E . (1)、求证: ;(2)、若 , ,求 的长.26. 在平面直角坐标系 中,抛物线 与x轴的交点为点 和点B .(1)、用含a的式子表示b;(2)、求抛物线的对称轴和点B的坐标;(3)、分别过点 和点 作x轴的垂线,交抛物线于点M和点N , 记抛物线在M , N之间的部分为图象G(包括M , N两点).记图形G上任意一点的纵坐标的最大值是m , 最小值为n .
(1)、求证: ;(2)、若 , ,求 的长.26. 在平面直角坐标系 中,抛物线 与x轴的交点为点 和点B .(1)、用含a的式子表示b;(2)、求抛物线的对称轴和点B的坐标;(3)、分别过点 和点 作x轴的垂线,交抛物线于点M和点N , 记抛物线在M , N之间的部分为图象G(包括M , N两点).记图形G上任意一点的纵坐标的最大值是m , 最小值为n .①当 时,求 的最小值;
②若存在实数t , 使得 ,直接写出a的取值范围.
27. 如图,在三角形 中, , , 是 边的高线,将线段 绕点A逆时针旋转 得到线段 ,连接 交 于点F . (1)、依题意补全图形,写出 °(2)、求 和 的度数;(3)、用等式表示线段 之间的数量关系,并证明.28. 对于平面直角坐标系 中的线段 ,给出如下定义:若存在 使得 ,则称 为线段 的“等幂三角形”,点R称为线段 的“等幂点”.
(1)、依题意补全图形,写出 °(2)、求 和 的度数;(3)、用等式表示线段 之间的数量关系,并证明.28. 对于平面直角坐标系 中的线段 ,给出如下定义:若存在 使得 ,则称 为线段 的“等幂三角形”,点R称为线段 的“等幂点”.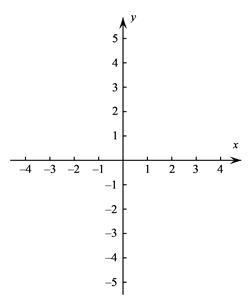 (1)、已知 .
(1)、已知 .①在点 中,线段 的“等幂点”是 ▲ ;
②若存在等腰 是线段 的“等幂三角形”,求点B的坐标;
(2)、已知点C的坐标为 ,点D在直线 上,记图形M为以点 为圆心,2为半径的 位于x轴上方的部分.若图形M上存在点E , 使得线段 的“等幂三角形” 为锐角三角形,直接写出点D的横坐标 的取值范围.