北京市门头沟区2022年中考一模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 如图是某个几何体的三视图,则该几何体是( )
 A、圆锥 B、圆柱 C、三棱柱 D、长方体2. 港珠澳大桥是世界上总体跨度最长的跨海大桥,全长55000米.其中海底隧道部分全长6700米,是世界最长的公路沉管隧道和唯一的深埋沉管隧道,也是我国第一条外海沉管隧道.将数字55000用科学记数法表示为()
A、圆锥 B、圆柱 C、三棱柱 D、长方体2. 港珠澳大桥是世界上总体跨度最长的跨海大桥,全长55000米.其中海底隧道部分全长6700米,是世界最长的公路沉管隧道和唯一的深埋沉管隧道,也是我国第一条外海沉管隧道.将数字55000用科学记数法表示为() A、 B、 C、 D、3. 如图, .点E在直线 上,点F在直线 上,过点E作 于E,如果 ,那么 的大小为( )
A、 B、 C、 D、3. 如图, .点E在直线 上,点F在直线 上,过点E作 于E,如果 ,那么 的大小为( )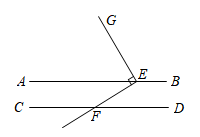 A、 B、 C、 D、4. 围棋起源于中国,古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战,截取对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、
A、 B、 C、 D、4. 围棋起源于中国,古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战,截取对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、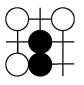 B、
B、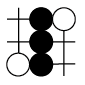 C、
C、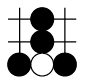 D、
D、 5. 实数a,b,c在数轴上对应点的位置如图所示,如果 ,下列结论中错误的是( )
5. 实数a,b,c在数轴上对应点的位置如图所示,如果 ,下列结论中错误的是( ) A、 B、 C、 D、6. 正五边形的内角和为()A、 B、 C、 D、7. 某数学兴趣小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的统计图,那么符合这一结果的实验最有可能的是()
A、 B、 C、 D、6. 正五边形的内角和为()A、 B、 C、 D、7. 某数学兴趣小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的统计图,那么符合这一结果的实验最有可能的是()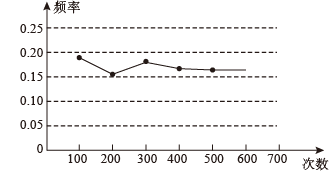 A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副只有四种花色的52张普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、抛掷一个质地均匀的正六面体骰子,向上的面点数是4 D、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球8. 如图,用一段长为18米的篱笆围成一个一边靠墙(墙长不限)的矩形花园,设该矩形花园的一边长为 ,另一边的长为 ,矩形的面积为 .当x在一定范围内变化时,y和S都随x的变化而变化,那么y与x.S与x满足的函数关系分别是()
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副只有四种花色的52张普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、抛掷一个质地均匀的正六面体骰子,向上的面点数是4 D、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球8. 如图,用一段长为18米的篱笆围成一个一边靠墙(墙长不限)的矩形花园,设该矩形花园的一边长为 ,另一边的长为 ,矩形的面积为 .当x在一定范围内变化时,y和S都随x的变化而变化,那么y与x.S与x满足的函数关系分别是() A、一次函数关系,二次函数关系 B、反比例函数关系,二次函数关系 C、一次函数关系,反比例函数关系 D、反比例函数关系,一次函数关系
A、一次函数关系,二次函数关系 B、反比例函数关系,二次函数关系 C、一次函数关系,反比例函数关系 D、反比例函数关系,一次函数关系二、填空题
-
9. 如果 在实数范围内有意义,那么实数x的取值范围是 .10. 分解因式:ax2-4ax+4a= .11. 写出一个比 大且比 小的整数 .12. 方程 的解为 .13. 石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB=m.
 14. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .15. 如图,点P在直线 外,点A、B、C、D均在直线 上,如果 ,只需添加一个条件即可证明 ,这个条件可以是(写出一个即可).
14. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .15. 如图,点P在直线 外,点A、B、C、D均在直线 上,如果 ,只需添加一个条件即可证明 ,这个条件可以是(写出一个即可). 16. 京西某游乐园的摩天轮采用了国内首创的横梁结构,是市民周末休闲的好去处.如图,如果该摩天轮的直径为88米,最高点A距地面100米,匀速运行一圈所需的时间是18分钟.但受周边建筑物影响,如果乘客与地面距离不低于34米时为最佳观景期,那么在摩天轮运行的一圈中最佳观景的时长为分钟.
16. 京西某游乐园的摩天轮采用了国内首创的横梁结构,是市民周末休闲的好去处.如图,如果该摩天轮的直径为88米,最高点A距地面100米,匀速运行一圈所需的时间是18分钟.但受周边建筑物影响,如果乘客与地面距离不低于34米时为最佳观景期,那么在摩天轮运行的一圈中最佳观景的时长为分钟.

三、解答题
-
17. 计算: .18. 解不等式组:19. 已知 ,求代数式 的值。20. 下面是小明设计“作圆的一个内接矩形,并使其对角线夹角为 ”尺规作图的过程.
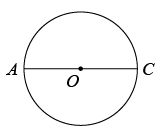
已知:如图, .
求作:矩形 ,使矩形 内接于 ,对角线 与 的夹角为
作法:①作 的直径 ;
②以点A为圆心, 长为半径作弧.交直线 上方的圆于点B;
③连接 并延长交 于点D;
④顺次连接 、 、 和 .
四边形 就是所求作的矩形,
根据小明设计的尺规作图过程
 (1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵点A,C都在 上,
, .
∴四边形 是平行四边形.( )(填推理依据).
又 是 的直径,
( )(填推理依据).
∴四边形 是矩形.
又 ▲ .
是等边三角形.
∴四边形 是所求作的矩形.
21. 如图,在平行四边形ABCD中, ,BE平分 交CD于O,交AD延长线于E,连接CE. (1)、求证:四边形BCED是菱形;(2)、若 , ,求 的面积.22. 在平面直角坐标系xOy中,已知点A(1,4),B(3,m).
(1)、求证:四边形BCED是菱形;(2)、若 , ,求 的面积.22. 在平面直角坐标系xOy中,已知点A(1,4),B(3,m). (1)、若点A , B在同一个反比例函数y1= 的图象上,求m的值;(2)、若点A , B在同一个一次函数y2=ax+b的图象上,
(1)、若点A , B在同一个反比例函数y1= 的图象上,求m的值;(2)、若点A , B在同一个一次函数y2=ax+b的图象上,①若m=2,求这个一次函数的解析式;
②若当x 3时,不等式mx﹣1 ax+b始终成立,结合函数图象,直接写出m的取值范围.
23. 某景观公园内人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是一条抛物线.现测量出如下数据,在距水枪水平距离为d米的地点,水柱距离湖面高度为h米.d(米)
0
1
2.0
3
…
h(米)
1.6
2.1
2.5
2.1
0
…
(1)、在下边网格中建立适当平面直角坐标系,根据已知数据描点,并用平滑曲线连接. (2)、结合表中所给数据或所画的图象,直接写出水柱最高点距离湖面的高度;(3)、求水柱在湖面上的落点距水枪的水平距离是多少?(4)、现公园想通过喷泉设立一个新的游玩项目.准备通过调节水枪高度使得公园的平顶游船能从喷泉最高点的正下方通过(两次水柱喷出水嘴的初速度相同),如果游船宽度为3米,顶棚到水面的高度为2米,为了避免游船被淋到,顶棚到水柱的垂直距离不小于0.8米.问应如何调节水枪的高度才能符合要求?请通过计算说明理由.24. 如图, 是 的直径,点D、E在 上, ,过点E作 的切线 ,交 的延长线于C.
(2)、结合表中所给数据或所画的图象,直接写出水柱最高点距离湖面的高度;(3)、求水柱在湖面上的落点距水枪的水平距离是多少?(4)、现公园想通过喷泉设立一个新的游玩项目.准备通过调节水枪高度使得公园的平顶游船能从喷泉最高点的正下方通过(两次水柱喷出水嘴的初速度相同),如果游船宽度为3米,顶棚到水面的高度为2米,为了避免游船被淋到,顶棚到水柱的垂直距离不小于0.8米.问应如何调节水枪的高度才能符合要求?请通过计算说明理由.24. 如图, 是 的直径,点D、E在 上, ,过点E作 的切线 ,交 的延长线于C.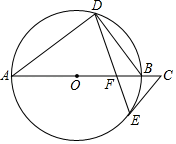 (1)、求证: ;(2)、如果 的半径为5. .求 的长.25. 电影《长津湖之水门桥》于2022年春节期间在全国公映,该片讲述了伟大的中国人民志愿军抗美援朝保家卫国的故事,为了解该影片的上座串,小丽统计了某影城1月31日至2月20日共三周该影片的观影人数(单位:人),相关信息如下:
(1)、求证: ;(2)、如果 的半径为5. .求 的长.25. 电影《长津湖之水门桥》于2022年春节期间在全国公映,该片讲述了伟大的中国人民志愿军抗美援朝保家卫国的故事,为了解该影片的上座串,小丽统计了某影城1月31日至2月20日共三周该影片的观影人数(单位:人),相关信息如下:a.1月31日至2月20日观影人数统计图:

b.1月31日至2月20日观影人频数统计图:

c.1月31日至2月20日观影人数在 的数据为t
91,92,93,93,95,98,99
根据以上信息,回答下列问题:
(1)、2月14日观影人数在这21天中从高到低排名第;(2)、这21天观影人数的中位数是;(3)、记第一周(1月31日至2月6日)观影人数的方差为 ,第二周(2月7日至2月13日)观影人数的方差为 ,第三周(2月14日至2月20日)观影人数的方差为 ,直接写出 , , 的大小关系.26. 在平面直角坐标系 中,已知抛物线 (m是常数). (1)、求该抛物线的顶点坐标(用含m代数式表示);(2)、如果该抛物线上有且只有两个点到直线 的距离为1,直接写出m的取值范围;(3)、如果点 , 都在该抛物线上,当它的顶点在第四象限运动时,总有 ,求a的取值范围.27. 如图,在等边 中,将线段 绕点A顺时针旋转 ,得到线段 .连接 ,作 的平分线 ,交 于E.
(1)、求该抛物线的顶点坐标(用含m代数式表示);(2)、如果该抛物线上有且只有两个点到直线 的距离为1,直接写出m的取值范围;(3)、如果点 , 都在该抛物线上,当它的顶点在第四象限运动时,总有 ,求a的取值范围.27. 如图,在等边 中,将线段 绕点A顺时针旋转 ,得到线段 .连接 ,作 的平分线 ,交 于E. (1)、①根据题意,补全图形;
(1)、①根据题意,补全图形;②请用等式写出 与 的数量关系,并证明.
(2)、分别延长 和 交于点F,用等式表示线段 , , 的数量关系,并证明.28. 我们规定:在平面直角坐标系 中,如果点P到原点O的距离为 ,点M到点P的距离是a的整数倍,那么点M就是点P的k倍关联点. (1)、当点 的坐标为 时,
(1)、当点 的坐标为 时,①如果点 的2倍关联点M在x轴上,那么点M的坐标是;
②如果点 是点 的k倍关联点,且满足 , .那么k的最大值为;
(2)、如果点 的坐标为 ,且在函数 的图象上存在 的2倍关联点,求b的取值范围.