安徽省淮北市2022年九年级中考模拟一数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 的相反数是A、 B、 C、 D、2. 2022年北京冬奥会是至今为止收视率最高的冬奥会!在全球社交媒体上吸引人数超20亿,其中20亿用科学记数法表示为()A、 B、 C、 D、3. 下列各式中正确的是()A、 B、 C、 D、4. 如图是由四个相同的小正方体组成的立体图形,它的俯视图是()
 A、
A、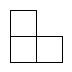 B、
B、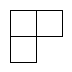 C、
C、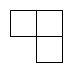 D、
D、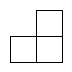 5. 如图,直线 , , ,则 等于( )
5. 如图,直线 , , ,则 等于( ) A、 B、 C、 D、6. 学习互助小组5个同学,某一天在课堂上的发言次数分别为6、7,8,9,10,关于这组数据,下列说法正确的是()A、平均数是7 B、众数是8 C、中位数是9 D、方差是27. 如图,直线 与x轴、y轴分别相交于A,B两点,过A,B两点作矩形 , ,曲线 在第一象限经过C,D两点,则k的值是( )
A、 B、 C、 D、6. 学习互助小组5个同学,某一天在课堂上的发言次数分别为6、7,8,9,10,关于这组数据,下列说法正确的是()A、平均数是7 B、众数是8 C、中位数是9 D、方差是27. 如图,直线 与x轴、y轴分别相交于A,B两点,过A,B两点作矩形 , ,曲线 在第一象限经过C,D两点,则k的值是( ) A、3 B、6 C、8 D、248. 在 中, , , , 平分 ,交 于点D,则 的长等于( )
A、3 B、6 C、8 D、248. 在 中, , , , 平分 ,交 于点D,则 的长等于( ) A、 B、 C、 D、79. 已知,a,b,5分别是等腰三角形三边的长,且a,b是关于x的一元二次方程 的两个根,则k的值等于()A、12 B、 C、12或 D、12或1310. 如图,在△ABC中,∠B=90°,AC=8,⊙O是△ABC的内切圆,分别与△ABC三边相切于点D , E , F , 设AD=x , △ABC的面积为S , 则S关于x的函数图象大致为( )
A、 B、 C、 D、79. 已知,a,b,5分别是等腰三角形三边的长,且a,b是关于x的一元二次方程 的两个根,则k的值等于()A、12 B、 C、12或 D、12或1310. 如图,在△ABC中,∠B=90°,AC=8,⊙O是△ABC的内切圆,分别与△ABC三边相切于点D , E , F , 设AD=x , △ABC的面积为S , 则S关于x的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 分解因式: .12. 不等式组 的解集是 .13. 如图,已知等边△ABC的边长为2,以AB为直径的⊙O与△ABC的边AC , BC分别相交于D , E两点,则扇形DOE的面积是 .
 14. 已知,抛物线y=−x2+(b+6)x+c , 其中b , c为实数.(1)、若抛物线经过点P(1,b),则c= .(2)、过点P作PA垂直y轴于点A , 交抛物线y=−x2+(b+6)x+c于另一点B , 点B在点A的右侧,若AB=3PA , 则抛物线上的点到x轴的最小距离是 .
14. 已知,抛物线y=−x2+(b+6)x+c , 其中b , c为实数.(1)、若抛物线经过点P(1,b),则c= .(2)、过点P作PA垂直y轴于点A , 交抛物线y=−x2+(b+6)x+c于另一点B , 点B在点A的右侧,若AB=3PA , 则抛物线上的点到x轴的最小距离是 .三、解答题
-
15. 计算:16. 《算法统宗》是中国古代数学名著之一,其中记载了这样的数学问题:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之绳多1尺,绳长井深各几何?”译文:“用绳子测水井深度,把绳子折成三折来量,井外余绳4尺;把绳子折成四折来量,井外余绳1尺,问绳长、井深各是多少尺?”请问此问题中的绳长、井深各是多少尺?17. 观察下列等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
…
请解答下列问题:
(1)、按以上规律列出第5个等式: = .(2)、用含有n的代数式表示第n个等式:(n为正整数);= .
(3)、求 的值.18. 如图,在平面直角坐标系中, 三个顶点的坐标分别为 、 、
( 1 )请画出 关于y轴 的对称图形 .
( 2 )请画出 关于点O成中心对称的图形 .
19. 某市为了加快5G网络信号覆盖,在市区附近小山顶部架设信号发射塔,如图所示.为了知道发射塔的高度,小兵从地面上的一点A测得发射塔顶端P点的仰角是45°,向山前走60米到达B点测得P点的仰角是60°,测得发射塔底部Q点的仰角是 .请你帮小兵计算出信号发射塔 的高度. 20. 如图,在 中, ,D是 上一点,过点A,C,D作 ,交 于点E,过点D作 ,交 于点F,连接 , , .求证:
20. 如图,在 中, ,D是 上一点,过点A,C,D作 ,交 于点E,过点D作 ,交 于点F,连接 , , .求证: (1)、四边形 是平行四边形.(2)、 .21. 阳光学校九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“诗歌”“散文”“其他”四个类别,每位同学仅选一项.根据调查结果,绘制了不完整的频数分布表和扇形统计图.
(1)、四边形 是平行四边形.(2)、 .21. 阳光学校九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“诗歌”“散文”“其他”四个类别,每位同学仅选一项.根据调查结果,绘制了不完整的频数分布表和扇形统计图.类别
频数(人数)
频率
小说
a
0.5
诗歌
4
散文
10
0.25
其他
6
合计
b
1

根据图表提供的信息,回答下列问题:
(1)、直接写出:a=;b=;m= .(2)、在调查问卷中,A、B、C、D四位同学选择了“诗歌”类,现从中任意选出2名同学参加学校的诗歌社团,请求出选取的2人恰好是B和C的概率.
