安徽省巢湖市2022年中考二模数学试题
试卷更新日期:2022-05-23 类型:中考模拟
一、单选题
-
1. 在-2,1,0, 中,其绝对值最大的数是( )A、-2 B、1 C、0 D、2. 下列运算正确的是()A、 B、 C、 D、3. 2020年是及其不平凡的一年,年初席卷全国的新冠疫情让全国上下都把全部注意力投向了卫生防疫方面,但是具有大无畏精神的安徽人民等到疫情局势稳定下来之后,就积极地恢复了各行各业的生产,从而创造了人间奇迹.安徽GDP正式发布,安徽省全年生产总值约3.88万亿元.其中“3.88万亿”用科学记数法可以表示为()A、 B、 C、 D、4. 下面的几何图形是由四个相同的小正方体搭成的,其中主视图和左视图相同的是( )A、
 B、
B、 C、
C、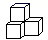 D、
D、 5. 下列因式分解正确的是()A、 B、 C、 D、6. 某十字路口有一组自动控制交通运行的红绿灯,按照绿灯亮30秒,黄灯亮5秒,红灯亮25秒循环显示.小明每天骑车上学都要经过这个路口,那么他一次路过此路口,正好遇到绿灯的概率是( )A、0.3 B、0.4 C、0.5 D、0.67. 已知一次函数 不经过第一象限,那么k , b的符号分别是( )A、 , B、 , C、 , D、 ,8. 秦杨商场去年第一季度销售利润是100万元,第二季度和第三季度的销售利润逐步攀升,第三季度销售利润是196万元.设第二季度和第三季度平均增长的百分率为x , 那么所列方程正确的是()A、 B、 C、 D、9. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
5. 下列因式分解正确的是()A、 B、 C、 D、6. 某十字路口有一组自动控制交通运行的红绿灯,按照绿灯亮30秒,黄灯亮5秒,红灯亮25秒循环显示.小明每天骑车上学都要经过这个路口,那么他一次路过此路口,正好遇到绿灯的概率是( )A、0.3 B、0.4 C、0.5 D、0.67. 已知一次函数 不经过第一象限,那么k , b的符号分别是( )A、 , B、 , C、 , D、 ,8. 秦杨商场去年第一季度销售利润是100万元,第二季度和第三季度的销售利润逐步攀升,第三季度销售利润是196万元.设第二季度和第三季度平均增长的百分率为x , 那么所列方程正确的是()A、 B、 C、 D、9. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )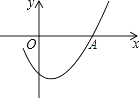 A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=010. 如图,在矩形ABCD中,AD=5,AB=3 ,点E在AB上, = ,在矩形内找一点P,使得∠BPE=60°,则线段PD的最小值为( )
A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=010. 如图,在矩形ABCD中,AD=5,AB=3 ,点E在AB上, = ,在矩形内找一点P,使得∠BPE=60°,则线段PD的最小值为( ) A、4 B、2 C、2 -2 D、2 -4
A、4 B、2 C、2 -2 D、2 -4二、填空题
-
11. 计算: .12. 命题“全等三角形的对应边都相等”的逆命题是命题.(填“真”或“假”)13. 将 代入反比例函数 中,所得函数值记为 ,又将 代入原反比例函数中,所得函数值记为 ,再将 代入原反比例函数中,所得函数值记为 ,……,如此继续下去,则 .14. 如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与 ABC相似时,运动的时间是 .

三、解答题
-
15. 解不等式: .16. 我国古代数学著作《算法统宗》中有这样一个问题,原文如下:三百七十八里关,初行健步不为难.次日脚疼减一半,六朝才得到其关.要见次日行里数,请公仔细算相还.大意为:有一个人走了378里路,第一天健步行走,从第二天起脚疼每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了多少里路?17. 如图是由边长为1的小正方形组成的网格,A、B、C、D四点均在正方形网格的格点上,线段AB、CD相交于点O .
 (1)、请在网格图中画出两条线段(不添加另外的字母),构成一对相似三角形,并用“∽”符号写出这对相似三角形:(2)、线段AO的长为 .18. 观察点阵图中点与等式之间的关系,寻找规律.
(1)、请在网格图中画出两条线段(不添加另外的字母),构成一对相似三角形,并用“∽”符号写出这对相似三角形:(2)、线段AO的长为 .18. 观察点阵图中点与等式之间的关系,寻找规律.① ;
② ;
③ ;
④ ;
…

按照你发现的规律解答下列问题:
(1)、第⑥个等式是;(2)、用含n(n为正整数)的等式表示第n个等式,并证明其正确性.19. 校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°. (1)、求A、B之间的路程;(参考数据: , )(2)、请判断此校车是否超过了白田路每小时60千米的限制速度?20. 如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D , 连接DB、DC .
(1)、求A、B之间的路程;(参考数据: , )(2)、请判断此校车是否超过了白田路每小时60千米的限制速度?20. 如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D , 连接DB、DC . (1)、求证:DB=DC=DI;(2)、若⊙O的半径为10cm,∠BAC=120°,求△BDC的面积.21. 某校为了解疫情期间学生自习课落实“停课不停学、学习不延期”在线学习的效果,校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种):A . 阅读电子教材,B . 听教师录播课程,C . 完成在线作业,D . 线上讨论交流.并根据调查结果绘制成如下两幅不完整的统计图,根据图中信息解答下列问题:
(1)、求证:DB=DC=DI;(2)、若⊙O的半径为10cm,∠BAC=120°,求△BDC的面积.21. 某校为了解疫情期间学生自习课落实“停课不停学、学习不延期”在线学习的效果,校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种):A . 阅读电子教材,B . 听教师录播课程,C . 完成在线作业,D . 线上讨论交流.并根据调查结果绘制成如下两幅不完整的统计图,根据图中信息解答下列问题: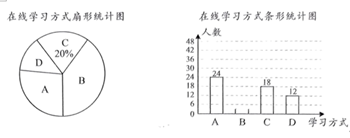 (1)、填空:校长本次调查的学生总人数为 , 并补全条形统计图;(2)、求扇形统计图中“D . 线上讨论交流”对应的圆心角的度数;(3)、若该校在线学习学生共有4000人,请你估计“B . 听教师录播课程”有多少人?22. 已知,一次函数 图象如图1所示,它的图象经过第一象限的点 , 轴于点M , 轴于点N , 且矩形MONP的周长为8.
(1)、填空:校长本次调查的学生总人数为 , 并补全条形统计图;(2)、求扇形统计图中“D . 线上讨论交流”对应的圆心角的度数;(3)、若该校在线学习学生共有4000人,请你估计“B . 听教师录播课程”有多少人?22. 已知,一次函数 图象如图1所示,它的图象经过第一象限的点 , 轴于点M , 轴于点N , 且矩形MONP的周长为8.
 (1)、求k的值;(2)、如图2,当 时,请求出抛物线 ( , )与直线 只有一个有公共点时,c的取值范围.23. 定义:如果一个三角形中有一个角是另一个角的2倍,那么我们称这样的三角形为倍角三角形.根据上述定义可知倍角三角形中有一个角是另一个角的2倍,所以我们就可以通过作出其中的2倍角的角平分线,得出一对相似三角形,再利用我们学过的相似三角形的性质解决相关问题.请通过这种方法解答下列问题:
(1)、求k的值;(2)、如图2,当 时,请求出抛物线 ( , )与直线 只有一个有公共点时,c的取值范围.23. 定义:如果一个三角形中有一个角是另一个角的2倍,那么我们称这样的三角形为倍角三角形.根据上述定义可知倍角三角形中有一个角是另一个角的2倍,所以我们就可以通过作出其中的2倍角的角平分线,得出一对相似三角形,再利用我们学过的相似三角形的性质解决相关问题.请通过这种方法解答下列问题: (1)、如图1,△ABC中,AD是角平分线,且 ,求证:△ABC是倍角三角形;(2)、如图2,已知△ABC是倍角三角形,且 , , ,求AC的长;(3)、如图3,已知△ABC中, , , ,求AC的长.
(1)、如图1,△ABC中,AD是角平分线,且 ,求证:△ABC是倍角三角形;(2)、如图2,已知△ABC是倍角三角形,且 , , ,求AC的长;(3)、如图3,已知△ABC中, , , ,求AC的长.