陕西省商洛市2022届高三下学期理数二模试卷

试卷更新日期：2022-05-23 类型：高考模拟

进入出卷网下载

一、单选题

1. $| {(3 - i)}^{2} | =$ （）

A、3 B、 $\sqrt{10}$ C、10 D、100

查看试题解析
2. 已知集合 $A = {x \in Z | x^{2} + x - 6 < 0}$ ， $B = {x | x > l n \frac{1}{2}}$ ，则集合 $A ∩ B$ 的子集有（）

A、2个 B、4个 C、8个 D、16个

查看试题解析
3. 若 $t a n θ = 2$ ，则 $c o s 2 θ =$ （）

A、 $- \frac{3}{5}$ B、 $- \frac{1}{3}$ C、 $\frac{3}{5}$ D、 $\frac{1}{3}$

查看试题解析
4. 若双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的两条渐近线与直线y＝2围成了一个等边三角形，则C的离心率为（）

A、 $\frac{3}{2}$ B、 $\sqrt{3} + 1$ C、 $\sqrt{3}$ D、2

查看试题解析
5. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} = (1 ， 1)$ ， $| \vec{b} | = 2$ ， $(\vec{a} - \vec{b}) \cdot \vec{a} = 1$ ，则 $| \vec{a} - \vec{b} | =$ （）

A、2 B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $2 \sqrt{3}$

查看试题解析
6. “圆柱容球”是指圆柱形容器里放了一个球，且球与圆柱的侧面及上、下底面均相切，则该圆柱的体积与球的体积之比为（）

A、2 B、 $\frac{3}{2}$ C、 $\sqrt{3}$ D、 $\frac{π}{3}$

查看试题解析
7. 数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …， $x_{m}$ 的平均数为 $\bar{x}$ ，数据 $y_{1}$ ， $y_{2}$ ， $y_{3}$ ， …， $y_{n}$ 的平均数为 $\bar{y}$ ，则数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …， $x_{m}$ ， $y_{1}$ ， $y_{2}$ ， $y_{3}$ ， …， $y_{n}$ 的平均数为（）

A、 $\frac{\bar{x}}{n} + \frac{\bar{y}}{m}$ B、 $\frac{\bar{x}}{m} + \frac{\bar{y}}{n}$ C、 $\frac{n \bar{x} + m \bar{y}}{m + n}$ D、 $\frac{m \bar{x} + n \bar{y}}{m + n}$

查看试题解析
8. 如图，A，B是函数 $f (x) = 2 s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的图象与x轴的两个交点，若 $| O B | - | O A | = \frac{4 π}{3}$ ，则 $ω =$ （）

A、1 B、 $\frac{1}{2}$ C、2 D、 $\frac{2}{3}$

查看试题解析
9. 甲､乙两人解关于x的方程 $2^{x} + b \cdot 2^{- x} + c = 0$ ，甲写错了常数b，得到的根为 $x = - 2$ 或x= $l o g_{2} \frac{17}{4}$ ，乙写错了常数c，得到的根为 $x = 0$ 或 $x = 1$ ，则原方程的根是（）

A、 $x = - 2$ 或 $x = l o g_{2} 3$ B、 $x = - 1$ 或 $x = 1$ C、 $x = 0$ 或 $x = 2$ D、 $x = - 1$ 或 $x = 2$

查看试题解析
10. 已知函数 $f (x)$ 满足 $f (x - π) = - f (- x)$ ，且函数 $f (x)$ 与 $g (x) = c o s x (x \neq - \frac{π}{2})$ 的图象的交点为 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ， $(x_{3} ， y_{3})$ ， $(x_{4} ， y_{4})$ ，则 $\sum_{i = 1}^{4} (x_{i} + y_{i}) =$ （）

A、－4π B、－2π C、2π D、4π

查看试题解析
11. 已知函数 $f (x) = l n x$ ，若对任意 $x_{1}$ ， $x_{2} \in (0 ， + \infty)$ ， $x_{1}^{2} [f (x_{1}) - f (x_{2})] \geq x_{2} (m x_{1} - x_{2})$ 恒成立，则m的最大值为（）

A、－1 B、0 C、1 D、e

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，已知圆 $O ： x^{2} + y^{2} = 1$ ，若曲线 $y = k | x - 1 | + 2$ 上存在四个点 $P_{i} (i = 1 ， 2 ， 3 ， 4)$ ，过动点Pi作圆O的两条切线，A，B为切点，满足 $\vec{P_{i} A} \cdot \vec{P_{i} B} = \frac{3}{2}$ ，则 $k$ 的取值范围为（）

A、 $(- ∞ ， - \frac{4}{3})$ B、 $(- \frac{4}{3} ， 0)$ C、 $(- \infty ， - 7) ∪ (- \frac{4}{3} ， - 1)$ D、 $(- 7 ， - \frac{4}{3}) ∪ (- 1 ， 0)$

查看试题解析

二、填空题

13. 若x，y满足约束条件 ${\begin{array}{l} x - y + 1 \geq 0 \\ 2 x + y - 4 \leq 0 \\ y \geq - 2 \end{array}$ ，则 $z = 2 y - x$ 的最大值为．

查看试题解析
14. △ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为1， $b^{2} + c^{2} - a^{2} = 4$ ，则A＝．

查看试题解析
15. 3名女生和4名男生随机站成一排，则每名女生旁边都有男生的概率为．

查看试题解析
16. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为4，点M是棱AB的中点，点P是底面ABCD内的动点，且P到平面 $A D D_{1} A_{1}$ 的距离等于线段PM的长度，则线段 $B_{1} P$ 长度的最小值为．

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 满足 $a_{1} = λ - 1$ ，且 $a_{n + 1} = λ a_{n} + 2 (λ \neq 0)$ ，且数列 ${a_{n} + 1}$ 是等比数列．

(1)、求 $λ$ 的值；

(2)、若 $b_{n} = a_{n} (a_{n} + 2)$ ，求 $b_{1} + b_{2} + b_{3} + \cdot \cdot \cdot + b_{n}$ ．

查看试题解析
18. 为落实党中央的“三农”政策，某市组织该市所有乡镇干部进行了一期“三农”政策专题培训，并在培训结束时进行了结业考试，从该次考试成绩中随机抽取样本，以 $[70 ， 75)$ ， $[75 ， 80)$ ， $[80 ， 85)$ ， $[85 ， 90)$ ， $[90 ， 95]$ 分组绘制的频率分布直方图如图所示．

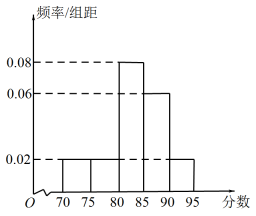(1)、根据频率分布直方图中的数据，估计该次考试成绩的平均数 $μ$ ；（同一组中的数据用该组区间的中点值作代表）

(2)、取（1）中 $μ$ 的值，假设本次考试成绩X服从正态分布 $N (μ ， σ^{2})$ ，且 $P (79 < X < 88) = 0.6$ ，从所有参加考试的乡镇干部中随机抽取3人，记考试成绩在 $(83.5 ， 88)$ 范围内的人数为Y，求Y的分布列及数学期望 $E (Y)$ ．

查看试题解析
19. 在四棱锥 $P - A B C D$ 中，底面ABCD为直角梯形， $A B / / C D$ ， $A B ⊥ B C$ ， $P D = B C = C D = 2 A B = 2 A P = 2$ ， E为 $C D$ 的中点，点P在平面 $A B C D$ 内的投影F恰好在直线 $A E$ 上．

(1)、证明： $C D ⊥ A P$ ．

(2)、求直线 $P B$ 与平面 $P A D$ 所成角的正弦值．

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ， $F_{1} (- 1 ， 0)$ 为其左焦点， $P (1 ， \frac{3}{2})$ 在椭圆 $C$ 上．

(1)、求椭圆C的方程．

(2)、若A，B是椭圆C上不同的两点，O为坐标原点，且 $\vec{O A} \cdot \vec{O B} = 0$ ，问△OAB的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

查看试题解析
21. 已知函数 $f (x) = (a - s i n x) e^{x} - x - a$ ．

(1)、若 $a = 0$ ，求曲线 $y = f (x)$ 在x＝0处的切线方程；

(2)、若 $f (x) \geq 0$ ，求a的取值范围．

查看试题解析
22. 在平面直角坐标系xOy中，曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = - 4 t^{2} \\ y = 4 t \end{array}$ （t为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线 $C_{2}$ 的极坐标方程为 $ρ = 2 c o s θ$ ．

(1)、求曲线 $C_{1}$ 与 $C_{2}$ 的直角坐标方程；

(2)、已知直线l的极坐标方程为 $θ = α (ρ \in R ， 0 < α < \frac{π}{2})$ ，直线l与曲线 $C_{1}$ ， $C_{2}$ 分别交于M，N（均异于点O）两点，若 $\frac{| O M |}{| O N |} = 4$ ，求 $α$ ．

查看试题解析
23. 已知函数 $f (x) = | x - m |$ ．

(1)、当m＝2时，解不等式 $f (x) - | x - 1 | > \frac{1}{2}$ ；

(2)、若函数 $f (x) = \frac{1}{x}$ 有三个不等实根，求实数m的取值范围．

查看试题解析