陕西省宝鸡市陈仓区2022届高三下学期理数二模试卷

试卷更新日期：2022-05-23 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x (2 - x) > 0} ，$ 集合 $B = {x | y = \sqrt{x - 2}}$ 则 $A \cup B =$ （）

A、(-∞，0)∪[2，+∞) B、(0，2] C、(0，2) D、(0，+∞)

查看试题解析
2. 若 $z (1 + i) = 1 - i$ ，则z=（）

A、 $1 - i$ B、 $1 + i$ C、 $- i$ D、 $i$

查看试题解析
3. 已知 $a ， b \in (0 ， 1)$ ，则函数 $f (x) = a x^{2} - 4 b x + 1$ 在 $[1 ， + \infty)$ 上是增函数的概率为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{2}{5}$ D、 $\frac{1}{4}$

查看试题解析
4. 北京天坛圜丘坛的地面由石板铺成，最中间的是圆形的天心石，围绕天心石的是扇环形的石板，从内到外各圈的石板数组成等差数列 ${a_{n}}$ ，它的前n项和为 $S_{n}$ ，且 $a_{2} = 18$ ， $a_{5} + a_{7} = 108$ ，则 $S_{21} =$ （）

A、2079 B、2059 C、2022 D、1890

查看试题解析
5. 设点 $A$ ， $B$ ， $C$ 不共线，则“ $| \vec{A B} + \vec{A C} | > | \vec{A B} - \vec{A C} |$ ”是“ $\vec{A B}$ 与 $\vec{A C}$ 的夹角是锐角”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 已知某圆锥的母线长为2，其轴截面为直角三角形，则下列关于该圆锥的说法中错误的是（）

A、圆锥的体积为 $\frac{2 \sqrt{2}}{3} π$ B、圆锥的表面积为 $2 \sqrt{2} π$ C、圆锥的侧面展开图是圆心角为 $\sqrt{2} π$ 的扇形 D、圆锥的内切球表面积为 $(24 - 16 \sqrt{2}) π$

查看试题解析
7. 若 $α \in （ 0, \frac{π}{2})$ , $\tan 2 α = \frac{\cos α}{2 - \sin α}$ ，则 $\tan α =$ （）

A、 $\frac{\sqrt{15}}{15}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\frac{\sqrt{15}}{3}$

查看试题解析
8. 如图是某届国际数学家大会的会标，现在有4种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同，则不同的涂色方案种数为（）

A、72 B、48 C、36 D、24

查看试题解析
9. 若函数 $f (x)$ 同时满足：①对于定义域上的任意x，恒有 $f (x) + f (- x) = 0$ ；②对于定义域上的任意 $x_{1}$ ， $x_{2}$ ，当 $x_{1} \neq x_{2}$ 时，恒有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ ，则称函数 $f (x)$ 为“理想函数”.下列四个函数中，能被称为“理想函数”的有（）
① $f (x) = \frac{1}{x}$ ，② $f (x) = \ln (\sqrt{1 + x^{2}} + x)$ ，③ $f (x) = \frac{1 - 2^{x}}{1 + 2^{x}}$ ，④ $f (x) = {\begin{matrix} - x^{2} ， x ⩾ 0 \\ x^{2} ， x < 0 \end{matrix}$

A、①② B、②③ C、③④ D、①④

查看试题解析
10. 天干地支纪年法源于中国，中国自古便有十天干与十二地支，十天干即甲､乙､丙､丁､戊､己､庚､辛､壬､癸；十二地支即子､丑､寅､卯､辰､已､午､未､申､酉､戌､亥.天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由“甲”起，地支由“子”起，例如，第一年为“甲子”，第二年为“乙丑”，第三年为“丙寅”…，以此类推，排列到“癸酉”后，天干回到“甲”重新开始，即“甲戌”，“乙亥”，然后地支回到“子”重新开始，即“丙子”…，以此类推，今年是壬寅年，也是中国社会主义青年团成立100周年，则中国社会主义青年团成立的那一年是（）

A、辛酉年 B、辛戎年 C、壬酉年 D、壬戌年

查看试题解析
11. 设抛物线 $C ： y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，准线为 $l$ ，点 $A$ 为 $C$ 上一点，以 $F$ 为圆心， $F A$ 为半径的圆交 $l$ 于 $B$ ， $D$ 两点，若 $∠ B F D = 120 °$ ， $A B D$ 的面积为 $2 \sqrt{3}$ ，则 p=（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} 10 x - m ， x \leq \frac{1}{2} \\ x e^{x} - 2 m x + m ， x > \frac{1}{2} \end{array}$ （e是自然对数的底数）在定义域R上有三个零点，则实数m的取值范围是（）

A、 $(e ， + \infty)$ B、 $(e ， 5]$ C、 $(e ， 5)$ D、 $[e ， 5]$

查看试题解析

二、填空题

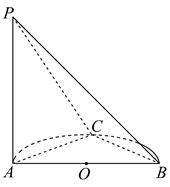
13. ${(x + \frac{2}{\sqrt{x}})}^{6}$ 的展开式中， $x^{3}$ 项的系数是(用数字作答）．

查看试题解析
14. 已知数列 ${a_{n}}$ 是等比数列，若 $2 a_{1} = a_{3} a_{4}$ ，且 $a_{5}$ 是 $a_{4}$ 与2的等差中项，则q的值是.

查看试题解析
15. 已知F是双曲线 $C ： x^{2} - y^{2} = 1$ 的右焦点，P是C的左支上一点， $A (0 ， \sqrt{2})$ .当 $△ A P F$ 周长最小时，该三角形的面积为.

查看试题解析
16. 如图，AB是半圆O的直径，点C在半圆上运动（不与A，B重合）， $P A ⊥$ 平面ABC，若 $A B = 2$ ，二面角 $A - B C - P$ 等于60°，则三棱锥P-ABC体积的最大值为.

查看试题解析

三、解答题

17. 心理学家发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学，给所有同学几何和代数各一题，让各位同学自由选择一道题进行解答，统计情况如下表：（单位：人）

	几何题	代数题	总计
男同学	22	8	30
女同学	8	12	20
总计	30	20	50

附表及公式：

$P (K^{2} \geq k_{0})$	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

$k^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

(1)、能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？

(2)、现从选择几何题的8名女生中任意抽取两人对他们的答题进行研究，记甲、乙两名女生被抽到的人数为

X

，求

X

的分布列及数学期望.

查看试题解析

18. a，b，c分别为钝角 $△ A B C$ 内角A，B，C的对边.已知 $3 a c o s A = b c o s C + c c o s B$ .

(1)、求 $c o s (A + \frac{π}{4})$ ；

(2)、若 $b = 2$ ， $c > b$ ，求c的取值范围.

查看试题解析
19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，四边形 $A A_{1} C_{1} C$ 是边长为 $4$ 的正方形， $A B = 3$ .再从条件①： $B C = 5$ 、条件②： $A B ⊥ A A_{1}$ 、条件③：平面 $A B C ⊥$ 平面 $A A_{1} C_{1} C$ 、中选择两个能解决下面问题的条件作为已知，并作答.

(1)、求证： $A B ⊥$ 平面 $A A_{1} C_{1} C$ ；

(2)、求直线 $B C$ 与平面 $A_{1} B C_{1}$ 所成角的正弦值.

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为 $F$ ，长半轴长为 $\sqrt{6}$ ，过焦点 $F$ 且垂直于 $x$ 轴的直线 $l$ 交椭圆于 $A ， B$ ， $| A B | = \sqrt{6}$ .

(1)、求椭圆 $C$ 的方程；

(2)、直线 $m$ 是圆 $O ： x^{2} + y^{2} = 1$ 的一条切线，且直线 $m$ 与椭圆 $C$ 相交于点 $M ， N$ ，求 $△ M O N$ 面积的最大值.

查看试题解析
21. 已知函数 $f (x) = x ln x - \frac{a}{2} x^{2} - x + 1$ ， $a \in R$ .

(1)、若函数 $y = f (x)$ 的图象在点 $(1 ， f (1))$ 处的切线方程为 $y = - 2 x + 1$ ，求实数a的值；

(2)、若函数 $f (x)$ 在定义域内有两个不同的极值点 $x_{1}$ ， $x_{2}$ .
（i）求实数a的取值范围；

（ii）当 $0 < m \leq 2$ 时，证明： $x_{1} + x_{2} > \frac{m}{a}$ .

查看试题解析
22. 在直线坐标系xOy中，曲线C₁： ${\begin{matrix} x = t c o s α \\ y = t s i n α \end{matrix}$ (t为参数，t≠0)其中 $0 \leq α \leq π$ .在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C₂：ρ＝2sinθ，C₃：ρ＝2 $\sqrt{3}$ cosθ.

(1)、求C₂与C₃交点的直角坐标；

(2)、若C₁与C₂相交于点A，C₁与C₃相交于点B，求|AB|的最大值．

查看试题解析
23. 设 $a ， b ， c ， d$ 均为正数，且 $a + b = c + d$ ，证明：
（Ⅰ）若 $a b > c d$ ，则 $\sqrt{a} + \sqrt{b} > \sqrt{c} + \sqrt{d}$ ；

（Ⅱ） $\sqrt{a} + \sqrt{b} > \sqrt{c} + \sqrt{d}$ 是 $| a - b | < | c - d |$ 的充要条件．

查看试题解析