山西省晋中市2022届高三下学期理数5月模拟试卷
试卷更新日期:2022-05-23 类型:高考模拟
一、单选题
-
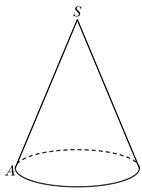
1. 已知 , ( 为虚数单位),则 等于( )A、1 B、-1 C、2 D、-22. 设集合 , ,则 等于( )A、 B、 C、 D、3. 设向量 , 满足 , , 与 的夹角为 ,则 等于( )A、2 B、1 C、3 D、4. 如图,已知圆锥的母线长 ,一只蚂蚁从 点出发绕着圆锥的侧面爬行一圈回到点 的最短距离为 ,则该圆锥的底面半径为( )
 A、1 B、2 C、 D、5. 我国古代数学巨著《九章算术》第三章中的“衰分”介绍了比例分配问题,“衰分”是指按比例递减分配的意思,通常称递减的比例为“衰分比”.如甲、乙、丙三人分配奖金的衰分比为20%,若甲分得奖金10000元,则乙、丙分得奖金分别为8000元和6400元.现有三名技术人员 , , 攻克了一项技术难题.若 , , 按照一定的“衰分比”分配奖金共75880元,其中 拿到了28000元,则“衰分比”为( )A、20% B、15% C、25% D、10%6. 北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断,这是一次中国文化与奥林匹克精神的完美结合.某商场决定派小王和小高等7名志愿者将两个吉祥物安装在大广场上,每人参与且只参与一个吉祥物的安装,每个吉祥物都至少由三名志愿者安装,若小王和小高必须安装不同的吉祥物,则不同的分配方案种数为( )A、40 B、30 C、20 D、807. 若 ,则 等于( )A、 B、2 C、-1 D、8. 已知抛物线 : 的焦点为 ,点 为 ,若射线 与抛物线 相交于点 ,与准线相交于点 ,且 ,则 的值为( )A、 B、 C、 D、9. 已知四棱锥 ,底面 为矩形, ,平面 平面 , 为正三角形.则四棱锥 的外接球的体积为( )A、 B、 C、 D、10. 数列 是递增的整数数列,若 , ,则 的最大值为( )A、25 B、22 C、24 D、2311. 已知 , 是双曲线 的左、右焦点,过点 作双曲线的一条渐近线的垂线,垂足为点 ,交另一条渐近线于点 ,且 ,则该双曲线的离心率为( )A、 B、3 C、 D、212. 设 , 为实数,且 ,函数 ,若对于任意 ,函数 有两个不同的零点,则 的取值范围是( )A、 B、 C、 D、
A、1 B、2 C、 D、5. 我国古代数学巨著《九章算术》第三章中的“衰分”介绍了比例分配问题,“衰分”是指按比例递减分配的意思,通常称递减的比例为“衰分比”.如甲、乙、丙三人分配奖金的衰分比为20%,若甲分得奖金10000元,则乙、丙分得奖金分别为8000元和6400元.现有三名技术人员 , , 攻克了一项技术难题.若 , , 按照一定的“衰分比”分配奖金共75880元,其中 拿到了28000元,则“衰分比”为( )A、20% B、15% C、25% D、10%6. 北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断,这是一次中国文化与奥林匹克精神的完美结合.某商场决定派小王和小高等7名志愿者将两个吉祥物安装在大广场上,每人参与且只参与一个吉祥物的安装,每个吉祥物都至少由三名志愿者安装,若小王和小高必须安装不同的吉祥物,则不同的分配方案种数为( )A、40 B、30 C、20 D、807. 若 ,则 等于( )A、 B、2 C、-1 D、8. 已知抛物线 : 的焦点为 ,点 为 ,若射线 与抛物线 相交于点 ,与准线相交于点 ,且 ,则 的值为( )A、 B、 C、 D、9. 已知四棱锥 ,底面 为矩形, ,平面 平面 , 为正三角形.则四棱锥 的外接球的体积为( )A、 B、 C、 D、10. 数列 是递增的整数数列,若 , ,则 的最大值为( )A、25 B、22 C、24 D、2311. 已知 , 是双曲线 的左、右焦点,过点 作双曲线的一条渐近线的垂线,垂足为点 ,交另一条渐近线于点 ,且 ,则该双曲线的离心率为( )A、 B、3 C、 D、212. 设 , 为实数,且 ,函数 ,若对于任意 ,函数 有两个不同的零点,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 命题 : , ,则 为.14. 若实数 , 满足约束条件 则 的最小值为.15. 点 在圆 : 上, , ,则 最大时, .16. 已知函数 ,给出下列四个命题:① 的图象关于 轴对称;②8为 的一个周期;③当 时, ;④ 在 上单调递增.其中真命题有(填序号).
三、解答题
-
17. 在 中,角 , , 所对的边分别为 , , .在① ;② ;③ 这三个条件中任选一个作为已知条件.(1)、求角 的大小;(2)、若 ,求 周长的最小值.18. 如图,在三棱锥 中, 为等腰直角三角形, , ,平面 平面 .
 (1)、求证: ;(2)、求二面角 的平面角的正弦值.19. 全球新冠肺炎疫情反反复复,国家卫健委专家建议大家出门时佩戴口罩.为了保障人民群众的生命安全和身体健康,某市质监局从药店随机抽取了500包某种品牌的口罩,测量其一项质量指标值 ,如下:
(1)、求证: ;(2)、求二面角 的平面角的正弦值.19. 全球新冠肺炎疫情反反复复,国家卫健委专家建议大家出门时佩戴口罩.为了保障人民群众的生命安全和身体健康,某市质监局从药店随机抽取了500包某种品牌的口罩,测量其一项质量指标值 ,如下:质量指标值
频数
10
45
110
165
120
40
10
(1)、求这500包口罩质量指标值的样本平均数 和样本方差 (同一组中的数据用该组区间的中点值作代表);(2)、口罩的质量指标值 服从正态分布 ,其中 近似为样本平均数 , 近似为样本方差 .①利用该正态分布,求 ;
②某人从该药店为本公司员工购买了100包这种品牌的口罩,记 表示这100包口罩中质量指标值 位于区间 的包数,利用①的结果,求 .
附: ,若 ,则 , , .
20. 已知椭圆 : 过点 ,过右焦点 作 轴的垂线交椭圆于M,N两点,且 .(1)、求椭圆 的方程;(2)、点P,Q在椭圆 上,且 , ,D为垂足.证明:存在定点 ,使得 为定值.