山东省德州市2022届高考数学二模试卷

试卷更新日期：2022-05-23 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {0 ， 1 ， 2}$ ， $B = {x | x^{2} + x - 2 \leq 0}$ ，则 $A \cap B =$ （）

A、 ${0 ， 1}$ B、 $[0 ， 1]$ C、 $[- 2 ， 1]$ D、 ${0 ， 1 ， 2}$

查看试题解析
2. 已知m，n是两条不重合的直线， $α$ 是一个平面， $n \subset α$ ，则“ $m ⊥ α$ ”是“ $m ⊥ n$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知i是虚数单位，a，b均为实数，且 $\frac{b + a i}{3 + i} = 1 - i$ ，则点(a，b)所在的象限为（）

A、一 B、二 C、三 D、四

查看试题解析
4. 已知 $a > 0$ ，二项式 ${(x + \frac{a}{x^{2}})}^{6}$ 的展开式中所有项的系数和为64，则展开式中的常数项为（）

A、36 B、30 C、15 D、10

查看试题解析
5. 要得到函数 $y = sin (2 x + \frac{π}{3})$ 的图象，只需将函数 $y = cos 2 x$ 的图象（）

A、向左平移 $\frac{π}{12}$ 个单位 B、向左平移 $\frac{π}{6}$ 个单位 C、向右平移 $\frac{π}{12}$ 个单位 D、向右平移 $\frac{π}{6}$ 个单位

查看试题解析
6. 设随机变量X服从正态分布N(1， $σ^{2}$ )，若 $P (X < 2 - a) = 0.3$ ，则 $P (2 - a < X < a) =$ （）

A、0.2 B、0.3 C、0.4 D、0.6

查看试题解析
7. 已知函数 $f (x)$ 是偶函数，其导函数 $f^{'} (x)$ 的图象见下图，且 $f (x + 2) = f (2 - x)$ 对 $x \in R$ 恒成立，则下列说法正确的是（）

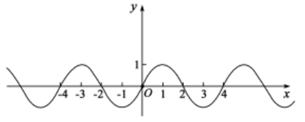A、 $f (- 1) < f (\frac{1}{2}) < f (\frac{5}{2})$ B、 $f (\frac{5}{2}) < f (\frac{1}{2}) < f (- 1)$ C、 $f (- 1) < f (\frac{5}{2}) < f (\frac{1}{2})$ D、 $f (\frac{1}{2}) < f (- 1) < f (\frac{5}{2})$

查看试题解析
8. 双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{16} = 1 (a > 0)$ 的一条渐近线方程为 $y = \frac{4}{3} x$ ， $F_{1}$ ， $F_{2}$ 分别为该双曲线的左右焦点， $M$ 为双曲线上的一点，则 $| M F_{2} | + \frac{16}{| M F_{1} |}$ 的最小值为（）

A、2 B、4 C、8 D、12

查看试题解析

二、多选题

9. 教育部办公厅“关于进一步加强中小学生体质健康管频率理工作的通知”中指出，各地要加强对学生体质健康0.06重要性的宣传，中小学校要通过体育与健康课程、大课间、课外体育锻炼、体育竞赛、班团队活动，家校协同联动等多种形式加强教育引导，让家长和中小学生007科学认识体质健康的影响因素．了解运动在增强体质、促进健康、预防肥胖与近视、锤炼意志、健全人格等方面的重要作用，提高学生体育与健康素养，增强体质健康管理的意识和能力，某学校共有2000名男生，为了了解这部分学生的身体发育情况，学校抽查了100名男生的体重情况．根据所得数据绘制样本的频率分布直方图如图所示，则（）

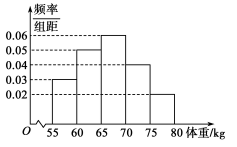A、样本的众数为 $67 \frac{1}{2}$ B、样本的80%分位数为72 $\frac{1}{2}$ C、样本的平均值为66 D、该校男生中低于60公斤的学生大约为300人

查看试题解析
10. 已知O为坐标原点， $A (\sqrt{3} ， 0)$ ， $B (\frac{\sqrt{3}}{2} ， \frac{3}{2})$ ， $P (\cos α ， \sin α) (0 \leq α \leq \frac{π}{3})$ ，则下列结论正确的是（）

A、 $△ O A B$ 为等边三角形 B、 $\vec{O P} \cdot \vec{O B}$ 最小值为 $\sqrt{3}$ C、满足 $\vec{O P} ⊥ \vec{A B}$ 的点P有两个 D、存在一点P使得 $\vec{P A} + \vec{P B} = \vec{O P}$

查看试题解析
11. 某地举办数学建模大赛，本次大赛的冠军奖杯由一个铜球和一个托盘组成，如图①，已知球的表面积为16 $π$ ，托盘由边长为8的等边三角形铜片沿各边中点的连线垂直向上折叠面成，如图②，则下列结论正确的是（）

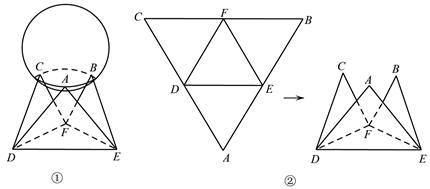A、直线AD与平面DEF所成的角为 $\frac{π}{3}$ B、经过三个顶点A，B，C的球的截面圆的面积为 $\frac{8 π}{3}$ C、异面直线AD与CF所成角的余弦值为 $\frac{5}{8}$ D、球上的点到底面DEF的最大距离为 $2 \sqrt{3} + \frac{\sqrt{6}}{3} + 2$

查看试题解析
12. 若函数 $f (x) = \ln x + a (x^{2} - 2 x + 1) (a \in R)$ 存在两个极值点 $x_{1} ， x_{2}$ $(x_{1} < x_{2})$ ，则（）

A、函数 $f (x)$ 至少有一个零点 B、 $a < 0$ 或 $a > 2$ C、 $0 < x_{1} < \frac{1}{2}$ D、 $f (x_{1}) + f (x_{2}) > 1 - 2 \ln 2$

查看试题解析

三、填空题

13. 设函数 ${\begin{matrix} x^{2} + 1 ， x \leq 0 \\ \ln x ， x > 0 \end{matrix}$ ，若 $f (a) = 1$ ，则 $a =$ ．

查看试题解析
14. 已知角θ的终边过点 $A (3 ， y)$ ，且 $\sin (π + θ) = \frac{4}{5}$ ，则tanθ= ．

查看试题解析
15. 已知抛物线 $x^{2} = 2 p y (p > 0)$ 的焦点为F，O为坐标原点，A(t，1)是抛物线第一象限上的点， $| A F | = 5$ ，直线AF与抛物线的另一个交点为B，则 $S_{△ A O B} =$ ．

查看试题解析
16. 十九世纪下半叶集合论的创立，奠定了现代数学的基础，著名的“康托三分集”是数学理性思维的构造产物，具有典型的分形特征，其操作过程如下：将闭区间[0，1]均分为三段，去掉中间的区间段 $(\frac{1}{3} ， \frac{2}{3})$ ，记为第1次操作；再将剩下的两个区间 $[0 ， \frac{1}{3}]$ ， $[\frac{2}{3} ， 1]$ 分别均分为三段，并各自去掉中间的区间段，记为第2次操作．．．；每次操作都在上一次操作的基础上，将剩下的各个区间分别均分为三段，同样各自去掉中间的区间段：操作过程不断地进行下去，剩下的区间集合即是“康托三分集”，第三次操作后，依次从左到右第三个区间为，若使前n次操作去掉的所有区间长度之和不小于 $\frac{26}{27}$ ，则需要操作的次数n的最小值为． ( $\lg 2 = 0.30$ ， $\lg 3 = 0.47$ )

查看试题解析

四、解答题

17. 已知数列{ $a_{n}$ }的首项 $a_{1} = \frac{1}{2}$ ，且满足 $a_{n + 1} = \frac{a_{n}}{3 - 2 a_{n}} (n \in N^{*})$ ．

(1)、证明 ${\frac{1}{a_{n}} - 1}$ 是等比数列，并求数列 $a_{n}$ 的通项公式；

(2)、记 $b_{n} = n (\frac{1}{a_{n}} - 1)$ ，求{ $b_{n}$ }的前n项和 $S_{n}$ ．

查看试题解析

18. 2021年12月17日，工信部发布的“十四五“促进中小企业发展规划》明确提出建立”百十万千”的中小企业梯度培育体系，引导中小企业走向“专精特新”、“小巨人”、“隐形冠军”的发展方向，“专精特新”是指具备专业化、精细化、特色化，新颖化优势的中小企业下表是某地各年新增企业数量的有关数据：

年份(年)	2017	2018	2019	2020	2021
年份代码(x)	1	2	3	4	5
新增企业数量：(y)	8	17	29	24	42

参考公式：回归方程 $\hat{y} = \hat{a} + \hat{b} x$ 中，斜率和截距最小二乘法估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$

(1)、请根据上表所给的数据，求出y关于x的线性回归方程，并预测2023年此地新增企业的数量；

(2)、若在此地进行考察，考察企业中有4个为“专精特新”企业，3个为普通企业，现从这7个企业中随机抽取3个，用X表示抽取的3个为“专精特新”全业个数，求随机变量X的分布列与期望．

查看试题解析

19. 在① $2 c = a \sin C + \sqrt{3} c \cos A$ ；② $\sqrt{3} \sin (A + C) \cos A = 3 \sin A \sin B$ ；③ $2 \cos A (c \cos B + b \cos C) = \sqrt{3} a$ ，这三个条件中任选一个，补充在下面问题中，并给出解答．
问题：已知 $△ A B C$ 中，D为AB边上的一点，且BD=2AD，___________．

(1)、若 $B = \frac{π}{6}$ ，求∠BCD大小；

(2)、若CD=CB，求cos∠ACB．
注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
20. 《九章算术》是中国古代张苍，耿寿昌所撰写的一部数学专著，是《算经十书》中最重要的一部，成于公元一世纪左右，是当时世界上最简练有效的应用数学专著，它的出现标志着中国古代数学形成了完整的体系．在《九章算术·商功》篇中提到“阳马”这一几何体，是指底面为矩形，有一条侧棱垂直于底面的四棱锥，现有“阳马” $P － A B C D$ ，底面为边长为2的正方形，侧棱 $P A$ ⊥面 $A B C D$ ， $P A = 2$ ，E、F为边 $B C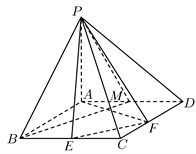$ 、 $C D$ 上的点， $\vec{C E} = λ \vec{C B}$ ， $\vec{C F} = λ \vec{C D}$ ，点M为AD的中点．

(1)、若 $λ = \frac{1}{2}$ ，证明：面PBM⊥面PAF；

(2)、是否存在实数 $λ$ ，使二面角 $P － E F － A$ 的大小为 $45^{\circ}$ ？如果不存在，请说明理由；如果存在，求此时直线 $B M$ 与面 $P E F$ 所成角的正弦值．

查看试题解析
21. 已知 $△ A B C$ 的两个顶点A，B的坐标分别为 $(- \sqrt{3} ， 0)$ ， $(\sqrt{3} ， 0)$ ，圆E是 $△ A B C$ 的内切圆，在边AC，BC，AB上的切点分别为P，Q，R， $| C P | = 2 - \sqrt{3}$ ，动点C的轨迹为曲线G．

(1)、求曲线G的方程；

(2)、设直线l与曲线G交于M、N两点，点D在曲线G上，O是坐标原点 $\vec{O M} + \vec{O N} = \vec{O D}$ ，判断四边形OMDN的面积是否为定值？若为定值，求出该定值；如果不是，请说明理由．

查看试题解析
22. 已知函数 $f (x) = \cos^{2} x + a (x^{2} - 1)$ ， $g (x) = 1 - \cos x$ ．

(1)、当 $a = 0$ 时，求 $f (x)$ 图象在( $\frac{π}{4}$ ，f( $\frac{π}{4}$ ))处的切线方程；

(2)、当 $a > 1$ 时，求 $f (x)$ 的极值；

(3)、若 $x \in (\frac{π}{2} ， π)$ ， $f^{'} (x)$ 为函数 $f (x)$ 的导数， $f^{'} (\frac{x}{2}) \geq g (x)$ 恒成立，求a的取值范围．

查看试题解析