浙江省衢州市常山县2022年九年级毕业考试调研数学试卷

试卷更新日期：2022-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 在－2，0，1， $\sqrt{2}$ 这四个数中，最小的数是（）

A、－2 B、0 C、1 D、 $\sqrt{2}$

查看试题解析
2. 由5个相同的小立方体搭成的几何体如图所示，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 如图，为测量B，C两地的距离，小娟在池塘外取点A，得到线段 $A B$ ， $A C$ ，并取 $A B$ ， $A C$ 的中点D，E，连结 $D E$ ．现测得 $D E$ 的长为6米，则B，C两地相距（）

A、3米 B、6米 C、9米 D、12米

查看试题解析
4. 下列运算正确的是（）

A、 ${(x^{2})}^{3} = x^{6}$ B、 $3 x^{2} - 2 x = x$ C、 ${(- 2 x)}^{3} = - 6 x^{3}$ D、 $x^{6} \div x^{2} = x^{3}$

查看试题解析
5. 含 $30 °$ 角的直角三角板与直线 $l_{1}$ 、 $l_{2}$ 的位置关系如图所示，已知 $l_{1}$ // $l_{2}$ ， $∠ A C D = ∠ A$ ，则 $∠ 1 =$ （）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
6. 一根排水管的截面如图所示，已知排水管的半径 $O B = 5$ ，水面宽 $A B = 8$ ，则截面圆心O到水面的距离为（）

A、2.5 B、3 C、3.5 D、4

查看试题解析
7. 如图， $∠ A B C$ 是一个锐角，以点A为圆心，适当长度为半径画弧，交射线 $B C$ 于点D，E，若 $∠ A B C = 35 ° ， ∠ B A D = 30 °$ ，则 $∠ D A E$ 的度数是（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
8. 如图，是小明连续两周居家记录的体温情况折线统计图，下列从图中获得的信息不正确的是（）

A、这两周体温的众数为 $36.6 ℃$ B、第一周平均体温高于第二周平均体温 C、第一周体温的中位数为 $37.1 ℃$ D、第二周的体温比第一周的体温更加平稳

查看试题解析
9. 如图，点A，B，C，D都在 $⊙ O$ 上， $B D$ 交 $A C$ 于点E， $\overset{⌢}{B C} = \overset{⌢}{C D} ， C E = 1 ， B C = 2$ ，则 $A E$ 的长为（）

A、2 B、3 C、4 D、5

查看试题解析
10. 汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”．如图，大正方形 $A B C D$ 由四个全等的直角三角形和一个小正方形组成，若 $∠ A D E = ∠ A E D$ ， $A D = 2 \sqrt{5}$ ，则 $△ A D E$ 的面积为（）

A、6 B、5 C、 $2 \sqrt{5}$ D、 $2 \sqrt{10}$

查看试题解析

二、填空题

11. 不等式 $x - 1 > 0$ 的解集是．

查看试题解析
12. 因式分解： $4 - a^{2} =$ ．

查看试题解析
13. 已知一个圆锥的底面半径为 $5cm$ ，母线长为 $6cm$ ，则这个圆锥的侧面积为 ${cm}^{2}$ ．

查看试题解析
14. 2022年是中国农历壬寅年，小阳同学利用一副七巧板拼出如图所示的“老虎”．已知七巧板拼成的正方形边长是4，则点A到直线 $B C$ 的距离为．

查看试题解析
15. 将一副三角板按如图方式放置在平面直角坐标系中，已知点A的坐标为 $(1 ， 0)$ ，斜边 $A B ⊥ x$ 轴，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象恰好经过点B，D，则点C的坐标为．

查看试题解析
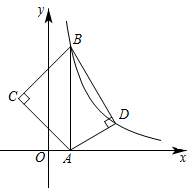16. “一切为了U”是常山在赶考共同富裕道路上，最新确定的城市品牌．已知线段 $A B$ ，对于坐标平面内的一个动点P，如果满足 $∠ A P B = 30 °$ ，则称点P为线段 $A B$ 的“U点”，如图，二次函数 $y = \frac{1}{2} x^{2} + 3 x + \frac{5}{2}$ 与x轴交于点A和点B．

(1)、线段 $A B$ 的长度为；

(2)、若线段 $A B$ 的“U”点落在y轴的正半轴上，则该“U点”的坐标为．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(2022)}^{0} + 2 \sin 30 ° - | - 1 |$ ．

(2)、 $\sqrt{27} - \sqrt{2} \times \sqrt{6}$ ．

查看试题解析

18. 小王和小凌在解答“解分式方程：

\frac{2 x + 3}{x} = 1 - \frac{x - 1}{x}

”的过程如下框，请你判断他们的解法是否正确？若错误，请写出你的解答过程.

小王的解法：

解，去分母得： $2 x + 3 = 1 - (x - 1)$ ①

去括号得： $2 x + 3 = 1 - x + 1$ ②

移项得： $2 x + x = 1 + 1 - 3$ ③

合并同类项得： $3 x = - 1$ ④

系数化为1得： $x = - \frac{1}{3}$ ⑤

$∴ x = - \frac{1}{3}$ 是原分式方程的解 ⑥

小凌的解法：

解，去分母得： $2 x + 3 = x - x - 1$ ①

移项得： $2 x = - 3 - 1$ ②

合并同类项得： $2 x = - 4$ ③

系数化为1得： $x = - 2$ ④

$∴ x = - 2$ 是原分式方程的解 ⑤

查看试题解析

19. 劳动教育是学校贯彻“五育并举”的重要举措，某校倡议学生在家帮助父母做一些力所能及的家务．小杨随机抽取该校部分学生进行问卷调查，问卷调查表如图所示，并根据调查结果绘制了两幅不完整的统计图．

(1)、求小杨共调查了多少人，并补全条形统计图．

(2)、该校有1500名学生，根据抽样调查结果，请你估计该校平均每周做家务的时间不少于2小时的学生人数．

(3)、为了增强学生的劳动意识，现需要从A组的四位同学中抽调两位同学参与到社区服务，已知A组共由两位女生、两位男生组成，请利用树状图或列表等方法求出恰好抽调到一男一女的概率．

查看试题解析
20. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以 $B D$ 为直径的半圆与交 $B C$ 于点F，点E是边 $A C$ 和半圆的公共点，且满足 $\overset{⌢}{D E} = \overset{⌢}{E F}$ ．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若 $∠ A = 30 °$ ， $A B = 9$ ，求 $\overset{⌢}{B F}$ 的长度．

查看试题解析
21. 图1是一种木质投石机模型，其示意图如图2所示．已知 $A B = A C ， B D = 4 cm ， B C = 8 cm$ ，木架 $A G = 8 cm$ ．弹绳在自然状态时，点A，E，D在同一直线上，按压点F旋转至点 $F^{'}$ ，抛杆 $E F$ 绕点A旋转至 $E^{'} F^{'}$ ，弹绳 $D E$ 随之拉伸至 $D E^{'}$ '，测得 $∠ C D E^{'} = ∠ B A E^{'} = 90 °$ ．

(1)、求 $∠ A D G$ 的度数．

(2)、求 $A E^{'}$ 的长度，

(3)、求点E转至点 $E^{'}$ 的过程中，点E垂直上升的高度．

查看试题解析
22. 某校的甲，乙两位老师同住一小区，该小区与学校相距1800米．甲从小区步行去学校，出发10分钟后乙再出发，乙从小区先骑公共自行车，途经学校又骑行若干米到达还车点后，立即以45米/分钟的速度步行到学校，设甲步行的时间为x（分钟），图中线段 $O A$ 和折线 $B - C - D$ 分别表示甲，乙离开小区的路程y米）与甲步行时间x（分钟）的函数关系的图象，根据图中所给信息，解答下列问题：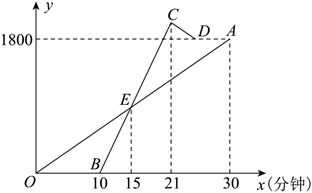

(1)、写出点E横坐标的实际意义，并求出点E的纵坐标．

(2)、求乙从还车点到学校所花的时间．

(3)、两人何时相距300米？

查看试题解析
23. 已知二次函数 $y = x^{2} + b x + 2 b$ （b为常数）．

(1)、若图象过 $(1 ， 4)$ ，求函数的表达式．

(2)、在（1）的条件下，当 $- 1 \leq x \leq 3$ 时，求函数的最大值和最小值．

(3)、若函数图象不经过第三象限，当 $- 4 \leq x \leq 1$ 时，函数的最大值和最小值之差为9，求b的值．

查看试题解析
24. 如图，将正方形纸片 $A B C D$ 折叠使点D落在射线 $B A$ 上的点E，将纸片展平，折痕交 $A D$ 边于点F，交 $B C$ 边于点G， $D C$ 的对应边 $E C^{'}$ 所在的直线交直线 $B C$ 于点H，连接 $D E$ ．

(1)、若点E在 $A B$ 边上，
①求证： $∠ A E D = ∠ D E H$ ．

②当 $\frac{A E}{E B} = \frac{2}{3}$ 时，求 $\sin ∠ B H E$ 的值．

(2)、若 $\frac{A E}{E B} = k$ ，求 $\frac{B H}{C H}$ 的值（用含k的代数式表示）．

查看试题解析