浙江省宁波市慈溪市2021-2022学年七年级下学期期中数学试卷
试卷更新日期:2022-05-20 类型:期中考试
一、选择题(本大题共10小题,共30.0分)
-
1. 下列现象中,不属于平移的是( )A、滑雪运动员在平坦的雪地上沿直线滑行 B、时针的走动 C、商场自动扶梯上顾客的升降运动 D、火车在笔直的铁轨上行驶2. 若关于 、 的方程 的一组解是 ,则 的值为( )A、-1 B、 C、1 D、23. 一种花粉颗粒直径约为0.0000065米,数字0.0000065用科学记数法表示为( )A、 B、 C、 D、4. 如图, 和 属于同位角的有( )
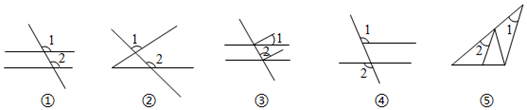 A、①②③ B、②③④ C、③④⑤ D、①②⑤5. 下列计算中,错误的是( )A、 B、 C、 D、6. 下列从左到右的变形属于因式分解的是( )A、 B、 C、 D、7. 如果 的乘积中不含 一次项,则 为( )A、5 B、-5 C、 D、8. 若 , ,则下列 , 关系式成立的是( )A、 B、 C、 D、9. 用如图 中的长方形和正方形纸板作侧面和底面,做成如图 的竖式和横式的两种无盖纸盒.现有 张正方形纸板和 张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则 的值可能是( )
A、①②③ B、②③④ C、③④⑤ D、①②⑤5. 下列计算中,错误的是( )A、 B、 C、 D、6. 下列从左到右的变形属于因式分解的是( )A、 B、 C、 D、7. 如果 的乘积中不含 一次项,则 为( )A、5 B、-5 C、 D、8. 若 , ,则下列 , 关系式成立的是( )A、 B、 C、 D、9. 用如图 中的长方形和正方形纸板作侧面和底面,做成如图 的竖式和横式的两种无盖纸盒.现有 张正方形纸板和 张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则 的值可能是( )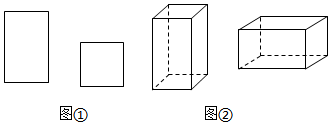 A、2019 B、2020 C、2021 D、202210. 如图①,现有边长为 和a+b的正方形纸片各一张,长和宽分别为 , 的长方形纸片一张,其中 .把纸片Ⅰ,Ⅲ按图②所示的方式放入纸片Ⅱ内,已知图②中阴影部分的面积满足 ,则 , 满足的关系式为( )
A、2019 B、2020 C、2021 D、202210. 如图①,现有边长为 和a+b的正方形纸片各一张,长和宽分别为 , 的长方形纸片一张,其中 .把纸片Ⅰ,Ⅲ按图②所示的方式放入纸片Ⅱ内,已知图②中阴影部分的面积满足 ,则 , 满足的关系式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 因式分解: .
12. 计算 .13. 小宁同学用 张边长为 的正方形纸片, 张边长为 的正方形纸片, 张邻边长分别为 、 的长方形纸片,拼出了邻边长分别为 、 的大长方形,那么小宁原来共有纸片张.14. 如图,在三角形 中,点 、 分别在边 、 上,将三角形 沿 折叠,使点 落在点 处,将线段 沿着 向右平移若干单位长度后恰好能与边 重合,连结 ,若 ,则阴影部分的周长为.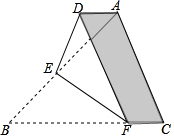 15. 如图,直线 分别与直线 , 相交于点 , , 平分 ,交直线 于点 ,若 ,射线 于点 ,则 的度数为度
15. 如图,直线 分别与直线 , 相交于点 , , 平分 ,交直线 于点 ,若 ,射线 于点 ,则 的度数为度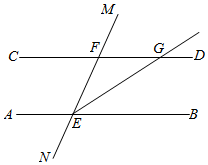 16. 若一个自然数能表示为两个相邻自然数的平方差,则这个自然数为“智慧效”,比如 , 就是智慧数.从0开始,不大于2022的智慧数共有个.
16. 若一个自然数能表示为两个相邻自然数的平方差,则这个自然数为“智慧效”,比如 , 就是智慧数.从0开始,不大于2022的智慧数共有个.三、解答题(本大题共8小题,共66.0分)
-
17. 计算:(1)、 .(2)、18. 先化简,后求值: ,其中 .19. 解下列方程组(1)、(2)、20. 阅读:已知 , ,求 的值.
解: , ,
.
请你根据上述解题思路解答下面问题:
(1)、已知 , ,求 的值.(2)、已知 ,求 的值.21. 如图, , .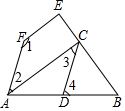 (1)、判定 与 的大小关系,并说明理由;(2)、若 平分 , 于点 , ,求 的度数.22. 已知关于 , 的方程组 ,其中 是实数.(1)、若方程组的解也是方程 的一个解,求 的值;(2)、求 为何值时,代数式 的值与 的取值无关,始终是一个定值,求出这个定值.23. 为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗
(1)、判定 与 的大小关系,并说明理由;(2)、若 平分 , 于点 , ,求 的度数.22. 已知关于 , 的方程组 ,其中 是实数.(1)、若方程组的解也是方程 的一个解,求 的值;(2)、求 为何值时,代数式 的值与 的取值无关,始终是一个定值,求出这个定值.23. 为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.
(1)、求医用口罩和洗手液的单价;(2)、由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.24. 如图,直线 ,一副三角尺 按如图 放置,其中点 在直线 上,点 , 均在直线 上,且 平分 .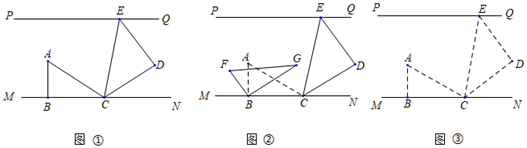 (1)、求 的度数.(2)、如图 ,若将三角形 绕点 以每秒 度的速度按逆时针方向旋转 的对应点分别为 , ,设旋转时间为 .
(1)、求 的度数.(2)、如图 ,若将三角形 绕点 以每秒 度的速度按逆时针方向旋转 的对应点分别为 , ,设旋转时间为 .在旋转过程中,若边 ,求 的值.
若在三角形 绕点 旋转的同时,三角形 绕点 以每秒2度的速度按顺时针方向旋转 的对应点为 , 请直接写出当边 时 的值.