浙江省宁波市鄞州区2022年初中学业水平模拟考试九年级数学试卷

试卷更新日期：2022-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022的倒数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、-2022 D、2202

查看试题解析
2. 下列计算正确的是（）

A、 $a^{4} - a^{2} = a^{2}$ B、 $a^{4} \div a^{2} = a^{2}$ C、 $a^{4} + a^{2} = a^{6}$ D、 $a^{4} • a^{2} = a^{8}$

查看试题解析
3. 2021年，宁波旅游总收入达到838.8亿元，逐步恢复疫情前水平，将该数用科学记数法表示是（）

A、 $838.8 \times 10^{8}$ B、 $8.388 \times 10^{10}$ C、 $0.8388 \times 10^{11}$ D、 $8.388 \times 10^{11}$

查看试题解析
4. 二次根式 $\sqrt{x - 3}$ 中，字母 $x$ 的取值范围是（）

A、 $x \geq 3$ B、 $x > 3$ C、 $x \neq 3$ D、 $x \leq - 3$

查看试题解析

5. 某班为推荐学生参加校数学素养展示活动，对4位学生的两个项目考核成绩如下表，若按照思维创新占80%，口头表达占20%计算总成绩，并根据总成绩择优推存，那么应推荐的学生是（）

项目	甲	乙	丙	丁
思维创新	90	95	100	95
口头表达	95	85	85	90

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 北京2022冬奥会吉样物“冰墩墩”和“雪容融”受到大家的喜爱，某网店出售这两种吉祥物礼品，借价如图所示.小明妈妈一共买10件礼品，总共花费不超过900元，如果设购买冰墩墩礼品 $x$ 件，则能够得到的不等式是（）

A、 $100 x + 80 (10 - x) > 900$ B、 $100 x + 80 (10 - x) < 900$ C、 $100 x + 80 (10 - x) \geq 900$ D、 $100 x + 80 (10 - x) \leq 900$

查看试题解析
7. 如图，一个空间几何体的主视图和左视图都是边长为2的正方形，俯视图是圆，关于这个几何体的说法错误的是（）

A、该几何体是圆柱 B、几何体底面积是 $4 π$ C、主视图面积是4 D、几何体侧面积是 $4 π$

查看试题解析
8. 如图，一次函数 $y_{1} = k_{1} x + b$ 的图象与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象交于点 $A (1 ， m)$ ， $B (4 ， n)$ .当 $y_{1} > y_{2}$ 时， $x$ 的取值范围是（）

A、 $1 < x < 4$ B、 $0 < x < 1$ 或 $x > 4$ C、 $x < 0$ 或 $1 < x < 4$ D、 $x < 0$ 或 $x > 4$

查看试题解析
9. 如图， $⊙ O$ 的半径为6，直径 $A B$ 垂直平分图内的线段 $C D$ ， $∠ C A O = 30^{\circ}$ ， $O C = 3 \sqrt{2}$ ，以点 $O$ 为圆心 $O C$ 为半径画扇形，则以下说法正确的是（）

A、 $∠ C O D$ 是 $120^{\circ}$ B、线段 $A D$ 的长为 $6 + \sqrt{6}$ C、 $\overset{⌢}{C D}$ 的长是 $5 π$ D、阴影部分的面积是 $7.5 π$

查看试题解析
10. 如图，正六边形 $A B C D E F$ 中，点 $P$ 是边 $A F$ 上的点，记图中各三角形的面积依次为 $S_{1} ， S_{2} ， S_{3} ， S_{4} ， S_{5}$ ，则下列判断正确的是（）

A、 $S_{1} + S_{2} = 2 S_{3}$ B、 $S_{1} + S_{4} = S_{3}$ C、 $S_{2} + S_{4} = 2 S_{3}$ D、 $S_{1} + S_{5} = S_{3}$

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
12. 分解因式： $2 m^{2} - 2$ = ．

查看试题解析
13. 在一个不透明的袋子里装着1个白球、2个黄球、4个红球，它们除颜色不同外其余都相同.现从袋中任意掵出一个球是红球的概率为.

查看试题解析
14. 如图，在平面直角坐标系中，双曲线 $y = \frac{m}{x}$ 在第一象限的分支经过 $R t △ A B C$ 的直角顶点 $C (5 ， 2) ， A C$ 平行 $y$ 轴，当顶点 $A ， B$ 能同时落在双曲线 $y = \frac{n}{x}$ 上时， $\frac{A C}{B C}$ 的值是.

查看试题解析
15. 如图，菱形 $A B C D$ 的边长为5，对角线 $A C$ 为8，以顶点 $D$ 为圆心，2为半径画圆，点 $P$ 在对角线上运动，当射线 $B P$ 与圆 $D$ 相切时， $A P$ 的长是.

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为4，正方形 $C E F G$ 的边长为 $2 \sqrt{2}$ ，将正方形 $C E F G$ 绕点 $C$ 旋转， $B G$ 和 $D E$ 相交于点 $K$ ，则 $A K$ 的最大值是，连结 $B E$ ，当点 $C$ 正好是 $△ B K E$ 的内心时， $C K$ 的长是.

查看试题解析

三、解答题

17.

(1)、解方程组： ${\begin{array}{l} x - y = 1 \\ \frac{1}{2} x + y = 2 \end{array}$

(2)、计算： $\frac{a + 4 b}{a + b} + \frac{2 a - b}{a + b}$

查看试题解析
18. 如图1是由边长为1的正方形构成的 $6 \times 5$ 的网格图，四边形 $A B C D$ 的顶点都在格点上.

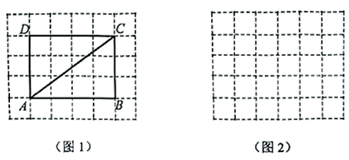(1)、求四边形 $A B C D$ 的对角线 $A C$ 的长；

(2)、命题“对角线相等的四边形一定是矩形”是真命题还是假命题？如果是假命题，请在图2中画一个顶点都是格点的四边形说明；如果是真命题，请进行证明.

查看试题解析
19. 如图1是可调节高度和桌面角度的电脑桌，它的左视图可以抽象成如图2所示的图形，底座 $A B$ 长为 $60 cm$ ，支架 $C D$ 垂直平分 $A B$ ，桌面 $E F$ 的中点 $D$ 固定在支架 $C D$ 处， $E F$ 宽为 $60 cm$ .身高为 $160 cm$ 的使用者 $M N$ 站立处点 $M$ 与点 $A ， B$ 在同一条直线上， $M A = 20 cm$ .点 $N$ 到点 $F$ 的距离是视线距离.

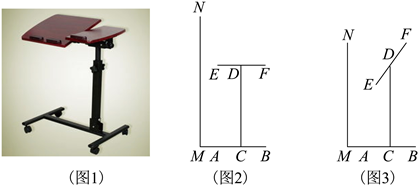(1)、如图2，当EF $∥$ AB， $C D = 100 cm$ 时，求视线距离 $N F$ 的长；

(2)、如图3，使用者坐下时，高度 $M N$ 下降 $50 cm$ ，当桌面 $E F$ 与 $C D$ 的夹角 $∠ C D E$ 为 $35^{\circ}$ 时，恰有视线NF $∥$ AB，问需要将支架 $C D$ 调整到多少 $cm$ ?（参考数据： $sin 35^{\circ} \approx 0.43 ， cos 35^{\circ} \approx 0.90 ， tan 35^{\circ} \approx 0.47$ ）

查看试题解析

20. 某校随机挑选了七年级中的一个班兴行了健身知识竞赛，满分100分，学生得分的最低分为50分，最高分为99分.如图是根据学生竞赛成绩绘制的频数分布表和频数分布直方图的一部分.

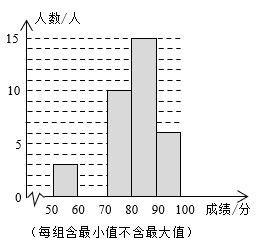
组别	频数	频率
$50 - 60$	3
$60 - 70$	$m$	0.15
$70 - 80$	10	0.25
$80 - 90$	15	$n$
$90 - 100$	6
合计

(1)、频数分布表中

60 \sim 70

这一组的频数

m

是，

80 \sim 90

这一组的频率

n

是.

(2)、本次健身知识竞赛成绩的中位数落在哪一组?

(3)、若成绩在60分及以上为通过，估计该校800名七年级学生健身知识竞赛通过的人数.

查看试题解析

21. 如图，抛物线 $C_{1} ： y = x^{2} + 2 x + c$ 与拋物线 $C_{2} ： y = x^{2} - 4 x + d$ 相交于点 $T$ ，点 $T$ 的横坐标为1.过点 $T$ 作 $x$ 轴的平行线交拋物线 $C_{1}$ 于点 $A$ ，交拋物线 $C_{2}$ 于点 $B$ .抛物线 $C_{1}$ 与 $C_{2}$ 分别与 $y$ 轴交于点 $C ， D$ .

(1)、求抛物线 $C_{1}$ 的对称轴和点 $A$ 的横坐标；

(2)、求线段 $A B$ 和 $C D$ 的长；

(3)、点 $P (- 2 ， p)$ 在抛物线 $C_{1}$ 上，点 $Q (5 ， q)$ 在抛物线 $C_{2}$ 上，请比较 $p$ 与 $q$ 的大小关系并说明理由.

查看试题解析
22. 如图是一次药物临床试验中受试者服药后学业中的药物浓度 $y$ （微克/毫升）与用药的时间 $x$ （小时）变化的图象.第一次服药后对应的图象由线段 $O A$ 和部分双曲线 $A B ： y = \frac{k}{x}$ 组成，服药6小时后血液中的药物浓度达到最高，16小时后开始第二次服药，服药后对应的图象由线段 $B C$ 和部分曲线 $C D ： y = \frac{k}{x - 16} + m$ 组成，其中 $O A$ 与 $B C$ 平行.血液中的浓度不低于5微克/毫升时有疗效.

(1)、分别求受试者第16小时，第22小时血液中的药物浓度；

(2)、受试者第一次服药后第二次服药前这16小时内，有疗效的持续时间达到6小时吗?

(3)、若血液中的药物浓度不高于4微克/毫升时才能进行第三次服药，问受试者第二次服药后至少经过几小时可进行第三次服药?

查看试题解析
23. 如图1，平行四边形 $A B C D$ 中， $A B = 9$ ， $B C = 12$ ，点 $P$ 是 $B C$ 边上的点，连结 $A P$ ，以 $A P$ 为对称轴作 $△ A B P$ 的轴对称图形 $△ A Q P$ .

(1)、如图2，当点 $Q$ 正好落在 $A D$ 边上时，判断四边形 $A B P Q$ 的形状并说明理由；

(2)、如图1，当点 $P$ 是线段 $B C$ 的中点且 $C Q = 4$ 时，求 $A P$ 的长；

(3)、如图3，当点 $P ， Q ， D$ 三点共线时，恰有 $∠ P Q C = ∠ P Q A$ ，求 $B P$ 的长.

查看试题解析
24. 如图1， $△ A B C$ 中， $B C$ 边上的中线 $A M = A C$ ，延长 $A M$ 交 $△ A B C$ 的外接圆于点 $D$ ，过点 $D$ 作DE $∥$ BC交圆于点 $E$ ，延长 $E D$ 交 $A B$ 的延长线于点 $F$ ，连结 $C E$ .

(1)、【特殊尝试】若 $∠ A C B = 60^{\circ}$ ， $B C = 4$ ，求 $M D$ 和 $D F$ 的长；

(2)、【规律探索】
①求证： $B C = 2 C E$ ；

②设 $tan ∠ A C B = x$ ， $\frac{F B}{A B} = y$ ，求 $y$ 关于 $x$ 的函数表达式：

(3)、【拓展应用】
如图2，作 $N C ⊥ A C$ 交线段 $A D$ 于 $N$ ，连结 $E N$ ，当 $△ A B C$ 的面积是 $△ C E N$ 面积的6倍时，求 $tan ∠ A C B$ 的值.

查看试题解析