浙江省杭州市萧山开发区2022年3月份中考模拟数学试卷（一模）

试卷更新日期：2022-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $2 \times (- 3) = 6$ B、 $0 - 2 = - 2$ C、 $\frac{1}{2} \times (- 2) = 1$ D、 $| - 2 | = - 2$

查看试题解析
2. 某几何体的三视图如图，则该几何体是（）

A、长方体 B、圆柱 C、球 D、正三棱柱

查看试题解析
3. 在平面内，下列数据不能确定物体位置的是（）

A、北偏东 $30 °$ B、钱塘明月 $4$ 号楼 $301$ 室 C、金惠路 $97$ 号 D、东经 $118 °$ ，北纬 $40 °$

查看试题解析
4. 如图，PA、PB是 $⊙ O$ 的切线，A、B为切点，连接OB、AB，若 $∠ A B O = 25 °$ ，则 $∠ A P B$ 的度数为（）

A、50° B、55° C、65° D、70°

查看试题解析
5. 京张高铁是2022年北京冬奥会的重要交通基础设施，考虑到不同路段的特殊情况，根据不同的运行区间设置不同的时速．其中，北京北站到清河段全长11千米，分为地下清华园隧道和地上区间两部分，运行速度分别设计为80千米/小时和120千米/小时，按此运行速度，地下隧道运行时间比地上大约多2分钟，如果设清华圆隧道全长为x千米，那么下面所列方程正确的是（）

A、 $\frac{x}{80} = \frac{11 - x}{120} + 2$ B、 $\frac{11 - x}{80} = \frac{x}{120} + \frac{1}{30}$ C、 $\frac{11 - x}{80} = \frac{x}{120} + 2$ D、 $\frac{x}{80} = \frac{11 - x}{120} + \frac{1}{30}$

查看试题解析
6. 共享单车已经成为城市公共交通的重要组成部分，某共享单车公司经过调查获得关于共享单车租用行驶时间的数据，并由此制定了新的收费标准：每次租用单车行驶a小时及以内，免费骑行；超过a小时后，每半小时收费1元，这样可保证不少于50%的骑行是免费的.制定这一标准中的a的值时，参考的统计量是此次调查所得数据的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 如图，点 $D$ ， $E$ ， $F$ 分别在 $△ A B C$ 的各边上，且 $D E / / B C$ ， $D F / / A C$ ，若 $A E$ ： $E C = 1$ ： $2$ ， $B F = 6$ ，则 $D E$ 的长为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知在平面直角坐标系xOy中，直线y＝2x＋2和直线 $y = \frac{2}{3} x + 2$ 分别交x轴于点A和点B.则下列直线中，与x轴的交点不在线段AB上的直线是（）

A、 $y = x + 2$ B、 $y = \sqrt{2} x + 2$ C、 $y = 4 x + 2$ D、 $y = \frac{2 \sqrt{3}}{3} x + 2$

查看试题解析
9. 公元3世纪，刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长．如图所示，他首先在圆内画一个内接正六边形，再不断地增加正多边形的边数；当边数越多时，正多边形的周长就越接近于圆的周长．刘徽在《九章算术》中写道：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”我们称这种方法为刘徽割圆术，它开启了研究圆周率的新纪元．小牧通过圆内接正 $n$ 边形，使用刘徽割圆术，得到π的近似值为（）

A、 $n \cdot \sin \frac{360 °}{2 n}$ B、 $2 n \cdot \sin \frac{360 °}{n}$ C、 $2 n \cdot \sin \frac{360 °}{2 n}$ D、 $n \cdot \sin \frac{360 °}{n}$

查看试题解析
10. 已知二次函数y＝﹣x²+2x+3，截取该函数图象在0≤x≤4间的部分记为图象G，设经过点（0，t）且平行于x轴的直线为l，将图象G在直线l下方的部分沿直线l翻折，图象G在直线上方的部分不变，得到一个新函数的图象M，若函数M的最大值与最小值的差不大于5，则t的取值范围是（　　）

A、﹣1≤t≤0 B、﹣1≤t $\leq - \frac{1}{2}$ C、 $- \frac{1}{2} \leq t \leq 0$ D、t≤﹣1或t≥0

查看试题解析

二、填空题

11. 分解因式： $m^{2} - 4 m + 4 =$ ．

查看试题解析
12. 已知 $2$ 、 $3$ 、 $4$ 、 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 的平均数是 $5$ ，则 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 的平均数是.

查看试题解析
13. 如图，这是某同学用纸板做成的一个底面直径为10cm，高为12cm的无底圆锥形玩具(接缝忽略不计)，则做这个玩具所需纸板的面积是cm²(结果保留 ).

查看试题解析
14. 如图，点O是半圆圆心， $B E$ 是半圆的直径，点A ， D在半圆上，且 $A D // B O ， ∠ A B O = 60 ° ， A B = 8$ ，过点D作 $D C ⊥ B E$ 于点C ，则阴影部分的面积是．

查看试题解析

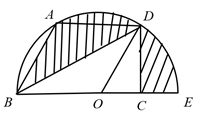15. 一个小球由静止开始在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离

s (

米

)

与时间

t (

秒

)

的数据如表：

时间 $t ($ 秒 $)$	1	2	3	4	$\dots$
距离 $s ($ 米 $)$	3	12	27	48	$\dots$

写出用 $t$ 表示 $s$ 的函数关系式：.

查看试题解析

16. 如图，点 $P$ 在平行四边形 $A B C D$ 的边 $B C$ 上，将 $△ A B P$ 沿直线 $A P$ 翻折，点 $B$ 恰好落在边 $A D$ 的垂直平分线 $M N$ 上，如果 $A B = 10$ ， $A D = 16$ ， $\tan B = \frac{4}{3}$ ，那么 $B P$ 的长为.

查看试题解析

三、解答题

17. 小明邀请你请参与数学接龙游戏：
【问题】解分式方程： $\frac{3 x}{x - 1} + \frac{x - 1}{3 x} = 2$ ，

【小明解答的部分】解：设 $\frac{3 x}{x - 1} = t$ ，则有 $\frac{x - 1}{3 x} = \frac{1}{t}$ ，故原方程可化为 $t + \frac{1}{t} = 2$ ，去分母并移项，得 $t^{2} - 2 t + 1 = 0$ .

【接龙】

查看试题解析
18. 某学校为了提高学生学科能力，决定开设以下校本课程： $A .$ 文学院， $B .$ 小小数学家， $C .$ 小小外交家， $D .$ 未来科学家，为了解学生最喜欢哪一项校本课程，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

(1)、这次被调查的学生共有人；

(2)、请你将条形统计图（2）补充完整；

(3)、在平时的小小外交家的课堂学习中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加全国英语口语大赛，求恰好同时选中甲、乙两位同学的概率 $($ 用树状图或列表法解答 $)$ .

查看试题解析
19. 下面是小西“过直线外一点作这条直线的垂线”的尺规作图过程.
已知：直线 $l$ 及直线 $l$ 外一点 $P$ .

求作：直线 $P Q$ ，使得 $P Q ⊥ l$ .

做法：如图，

①在直线 $l$ 的异侧取一点 $K$ ，以点 $P$ 为圆心， $P K$ 长为半径画弧，交直线 $l$ 于点 $A$ ， $B$ ；

②分别以点 $A$ ， $B$ 为圆心，大于 $\frac{1}{2} A B$ 的同样长为半径画弧，两弧交于点 $Q ($ 与 $P$ 点不重合 $)$ ；

③作直线 $P Q$ ，则直线 $P Q$ 就是所求作的直线.

根据小西设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形； $($ 保留作图痕迹 $)$

(2)、完成 $P Q ⊥ l$ 的证明.

查看试题解析
20. 实验数据显示，一般成人喝半斤低度白酒后，1.5时内其血液中酒精含量y(毫克／百毫升)与时间 $x$ (时)的关系可近似地用二次函数 $y = - 200 x^{2} + 400 x$ 刻画；1.5时后(包括1.5时)y与x可近似地用反比例函数 $y = \frac{k}{x}$ (k＞0)刻画(如图所示).

(1)、根据上述数学模型计算：
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?

②当 $x$ ＝5时，y＝45.求k的值.

(2)、按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克／百毫升时属于“酒后驾驶”，不能驾车上路.参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班?请说明理由.

查看试题解析
21. 已知：如图，边长为 $4$ 的菱形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ，若 $∠ C A D = ∠ D B C$ .

(1)、求证：四边形 $A B C D$ 是正方形.

(2)、 $E$ 是 $O B$ 上一点， $B E = 1$ ，且 $D H ⊥ C E$ ，垂足为 $H$ ， $D H$ 与 $O C$ 相交于点 $F$ ，求线段 $O F$ 的长.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a {(x - h)}^{2} - 8 a$ 的顶点为 $A$ ， $h > 0$ .

(1)、若 $a = 2$ ，
①点 $A$ 到 $x$ 轴的距离为▲ ；

②求此抛物线与 $x$ 轴的两个交点之间的距离；

(2)、已知点 $A$ 到 $x$ 轴的距离为 $4$ ，若此抛物线与直线 $y = - x + 1$ 必有两个交点，分别为 $B (x_{1} ， y_{1})$ ， $C (x_{2} ， y_{2})$ ，其中 $x_{1} < x_{2}$ ，若点 $D (x_{D} ， y_{D})$ 在此抛物线上，当 $x_{1} < x_{D} < x_{2}$ 时， $y_{D}$ 总满足 $y_{2} < y_{D} < y_{1}$ ，求 $a$ 的值和 $h$ 的取值范围.

查看试题解析
23. 在圆 $O$ 中，弦 $A B$ 与 $C D$ 相交于点 $E$ ，且弧 $A C$ 与弧 $B D$ 相等.点 $D$ 在劣弧 $A B$ 上，连接 $CO$ 并延长交线段 $A B$ 于点 $F$ ，连接 $O A$ 、 $O B$ .

(1)、求证： $△ O F A$ ∽ $△ E F C$ ；

(2)、当 $O A = 5$ ，且 $tan ∠ O A B = \frac{1}{2}$ 时，如果 $△ A O F$ 是直角三角形，求线段 $E F$ 的长.

查看试题解析