浙江省杭州市建德市2022届九年级下学期期中数学试卷(一模)
试卷更新日期:2022-05-20 类型:中考模拟
一、单选题
-
1. ( )A、 B、 C、 D、2. 如图,是一个几何体的表面展开图,则该几何体是( )
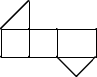 A、正方体 B、长方体 C、三棱柱 D、四棱锥3. 二次函数 的对称轴为( )A、直线 B、直线 C、直线 D、直线4. 一个不透明的盒子中装有5个大小相同的乒乓球,做了1000次摸球实验,摸到黄球的频数为401,则估计其中的黄球个数为( )A、1 B、2 C、3 D、45. 在 的内部任取一点C,作射线OC,则一定有( )A、 B、 C、 D、6. 我校在举办“图书节”的活动中,将 本图书分给了 名学生,若每人分6本,则剩余40本;若每人分8本,则还缺50本,下列方程正确的是( )A、 B、 C、 D、7. 如图,直线 ,在某平面直角坐标系中, 轴 , 轴 ,点 的坐标为 ,点 的坐标为 ,则坐标原点为( )
A、正方体 B、长方体 C、三棱柱 D、四棱锥3. 二次函数 的对称轴为( )A、直线 B、直线 C、直线 D、直线4. 一个不透明的盒子中装有5个大小相同的乒乓球,做了1000次摸球实验,摸到黄球的频数为401,则估计其中的黄球个数为( )A、1 B、2 C、3 D、45. 在 的内部任取一点C,作射线OC,则一定有( )A、 B、 C、 D、6. 我校在举办“图书节”的活动中,将 本图书分给了 名学生,若每人分6本,则剩余40本;若每人分8本,则还缺50本,下列方程正确的是( )A、 B、 C、 D、7. 如图,直线 ,在某平面直角坐标系中, 轴 , 轴 ,点 的坐标为 ,点 的坐标为 ,则坐标原点为( ) A、点A B、点B C、点C D、点D8. 已知点 在直线 上,且 ,则( )A、 有最大值 B、 有最小值 C、 有最大值 D、 有最小值9. 如图,已知 切 于点 ,点 在 上,且 ,连结 并延长交 于点 , 的半径为2,设 ,
A、点A B、点B C、点C D、点D8. 已知点 在直线 上,且 ,则( )A、 有最大值 B、 有最小值 C、 有最大值 D、 有最小值9. 如图,已知 切 于点 ,点 在 上,且 ,连结 并延长交 于点 , 的半径为2,设 ,
①当m= 时, 是等腰直角三角形;②若 ,则 ;③当 时, 与 相切.以上列选项正确的有( )
A、② B、③ C、②③ D、①③10. 已知代数式 化简后为一个完全平方式,且当 时此代数式的值为0,则下列式子中正确的是( )A、 B、 C、 D、二、填空题
-
11. 任意一个十边形的内角和为 .12. 化简: .13. 小明上下学的交通工具是公交车,上学、放学都可以坐3路、5路和7路这三路车中的一路,则小明当天上学、放学坐的是同一路车的概率为.14. 如图,在 中, , , ,则 的长为.
 15. 已知反比例函数的表达式为 , 和 是反比例函数图象上两点,若 时, ,则 的取值范围是.16. 如图,已知矩形 ,将 绕点 顺时针旋转 至 ,连结 ,BF,若点A,C, 恰好在同一条直线上,则 .
15. 已知反比例函数的表达式为 , 和 是反比例函数图象上两点,若 时, ,则 的取值范围是.16. 如图,已知矩形 ,将 绕点 顺时针旋转 至 ,连结 ,BF,若点A,C, 恰好在同一条直线上,则 .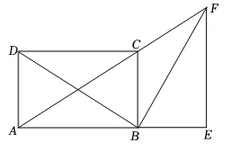
三、解答题
-
17. 下面是小明同学解不等式的过程,
解不等式:
解:
你认为正确吗?错误的话,请你写出正确的做法.
18. 农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
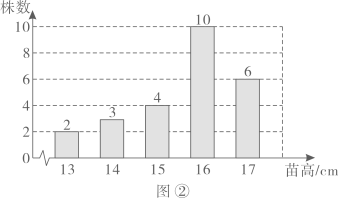
请根据相关信息,解答下列问题:
(1)、本次抽取的麦苗的株数为 , 图①中m的值为;(2)、求统计的这组苗高数据的平均数、众数和中位数.19. 如图, 为锐角,射线 ∥射线 ,作 和 的平分线分别交 和 于点 和 ,连接 ,求证:四边形 为菱形. 20. 已知:一次函数 的图象与某反比例函数的图象的一个公共点的横坐标为1.(1)、求该反比例函数的解析式;(2)、将一次函数 的图象向上平移4个单位,求平移后的图象与反比例函数图象的交点坐标.21. 如图, 中, ,点 是边 的中点,以 为底边在其右侧作等腰三角形 ,使 ,连结 ,则:
20. 已知:一次函数 的图象与某反比例函数的图象的一个公共点的横坐标为1.(1)、求该反比例函数的解析式;(2)、将一次函数 的图象向上平移4个单位,求平移后的图象与反比例函数图象的交点坐标.21. 如图, 中, ,点 是边 的中点,以 为底边在其右侧作等腰三角形 ,使 ,连结 ,则: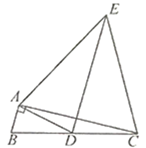 (1)、求证: ;(2)、若 ,求证: .
(1)、求证: ;(2)、若 ,求证: .
