陕西省渭南市澄城县2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-05-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{8}$ C、 $\sqrt{16}$ D、 $\sqrt{18}$

查看试题解析
2. 下列各组数中，是勾股数的为（）

A、1，1， $\sqrt{2}$ B、5，12，13 C、1.5，2，2.5 D、7，8，9

查看试题解析
3. 下列式子能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{12}$ B、 $\sqrt{20}$ C、 $\sqrt{32}$ D、 $\sqrt{38}$

查看试题解析
4. 在▱ABCD中，∠A=3∠B，则∠B的度数是（）

A、30° B、36° C、45° D、60°

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{7} = \sqrt{10}$ B、 $2 \sqrt{7} - 5 \sqrt{7} = 3 \sqrt{7}$ C、 $\sqrt{2} \times \sqrt{8} = 2 \sqrt{2}$ D、 $\sqrt{27} \div \sqrt{3} = 3$

查看试题解析
6. 矩形具有而菱形不一定具有的性质是（）

A、两组对边分别平行 B、对角线相等 C、对角线互相垂直 D、对角线平分一组对角

查看试题解析
7. 如图，长方体的长为15，宽为10，高为20，点B在棱上且离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）

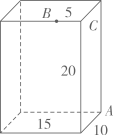A、25 B、5 $\sqrt{29}$ C、 $10 \sqrt{5} + 5$ D、5 $\sqrt{37}$

查看试题解析
8. 如图，在等腰直角△ABC中， $∠ B A C = 90^{\circ}$ ，D、E是BC上的两点，且BD＝CE，过D、E作DM、EN分别垂直AB、AC，垂足为M、N，延长MD、NE交于点F，连接AD、AE.其中：①四边形AMFN是正方形；②△ABE $≅$ △ACD；③当 $∠ D A E = 45^{\circ}$ 时， $C E^{2} + B D^{2} = D E^{2}$ ，正确的结论有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

9. 计算 $\sqrt{{(- \frac{1}{2})}^{2}}$ 的结果是．

查看试题解析
10. 命题“如果 $a + b > 0$ ，则 $a > 0$ ， $b > 0$ ”的逆命题为.

查看试题解析
11. 如图，O点为数轴原点，A点对应的数是3， $O B ⊥ O A$ ，连接AB， $A B = 4$ ，以O为圆心，OB长为半径画弧交数轴正半轴于点C，则点C对应的实数为.

查看试题解析
12. 如图， $∠ A C B = 90^{\circ}$ ，D为AB的中点，点E为AF的中点，使E、C、D共线，且 $C E = \frac{1}{4} C D$ ，若 $B F = 10$ ，则AB的长为.

查看试题解析
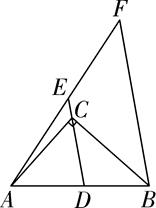13. 如图，菱形ABCD的周长为16， $∠ D A B = 60^{\circ}$ ，点E为BC边的中点，点P为对角线AC上一动点，连接BP、EP，则 $P B + P E$ 的最小值为.

查看试题解析

三、解答题

14. 计算： ${(2 \sqrt{3} - 1)}^{2} + \sqrt{18} \div \sqrt{6} + \sqrt{48}$

查看试题解析
15. 如图， $▱$ ABCD的对角线AC、BD相交于点O，若AC＝10cm，BD＝18cm，CD＝7cm，求△AOB的周长.

查看试题解析
16. 如图，一座城墙高BC＝11.7m，墙外有一条宽AB为9m的护城河，那么一架长为15m的梯子能否到达墙的顶端C？

查看试题解析
17. 高空抛物极其危险，是我们必须杜绝的行为.据研究，高空抛出的物体下落的时间t（单位：s）和高度h（单位：m）近似满足 $t = \sqrt{\frac{h}{5}}$ （不考虑风速的影响）.

(1)、从200m高空抛物到落地所需时间t是多少？

(2)、从高空抛物经过3s落地，该物体下落的高度是多少？

查看试题解析
18. 如图，已知在 $△ A B C$ 中， $A B = 12 ， A C = 10 ， B C$ 边上的高 $A D = 8 ，$ 求 $B C$ 边的长.

查看试题解析
19. 已知 $a = \sqrt{6} + \sqrt{2}$ ， $b = \sqrt{6} - \sqrt{2}$ ，求 $a^{2} b - a b^{2}$ 的值.

查看试题解析
20. 如图，已知平行四边形ABCD中，点E为BC边的中点，连DE并延长DE交AB延长线于点F，求证：四边形DBFC是平行四边形.

查看试题解析
21. 如图， $△ A B C$ 在正方形网格中，若小方格的边长均为1，试判断 $△ A B C$ 的形状，并说明理由.

查看试题解析
22. 小明家装修，电视背景墙长BC为 $\sqrt{27}$ m，宽AB为 $\sqrt{8}$ m，中间要镶一个长为2 $\sqrt{3}$ m宽为 $\sqrt{2}$ m的长方形大理石图案（图中阴影部分）.除去大理石图案部分，其他部分贴壁布，求壁布的面积（结果化为最简二次根式）

查看试题解析
23. 如图，在四边形ABCD中， $A B ∥ C D$ ， $A B = B C = 2 C D$ ，E为对角线AC的中点，F为边BC的中点，连接DE、EF.

(1)、求证：四边形CDEF为菱形；

(2)、连接DF交AC于点G，若 $D F = 2$ ， $C D = \frac{5}{3}$ ，求四边形CDEF的面积.

查看试题解析
24. 如图，小巷左右两侧是竖直的高度相等的墙，一个竹竿斜靠在左墙时，竹竿底端O到左墙角的距离OC为0.7米，顶端B距墙顶A的距离AB为0.6米.如果保持竹竿底端位置不动，将竹竿斜靠在右墙时，竹竿底端到右墙角的距离OF为1.5米，顶端E距墙顶D的距离DE为1米，点A、B、C在一条直线上，点D、E、F在一条直线上， $A C ⊥ C F$ ， $D F ⊥ C F$ ，则墙的高度为多少米？

查看试题解析
25. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作 $A E ⊥ B C$ 于点E，延长BC至F，使 $C F = B E$ .连接DF.

(1)、求证：四边形ADFE为矩形；

(2)、连接OF，若 $A D = 3$ ， $E C = 2$ ， $∠ A B F = 60^{\circ}$ ，求OF的长.

查看试题解析
26. 在正方形ABCD中，点E是对角线AC上一点，点F是正方形ABCD外角平分线CM上一点，且CF＝AE，连接BE，EF.

(1)、如图1，当E是线段AC的中点时，BE与EF有何数量关系，并证明；

(2)、当点E不是线段AC的中点，其它条件不变时，请你在图2中补全图形，判断（1）中的结论是否仍然成立，并证明你的结论.

查看试题解析