陕西省宝鸡市凤翔县2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2022-05-20 类型:期中考试
一、单选题
-
1. 下列轴对称图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 满足下列条件的△ABC,不是直角三角形的是( )A、∠A:∠B:∠C=5:12:13 B、a:b:c=3:4:5 C、∠C=∠A﹣∠B D、b2=a2﹣c23. 用不等式表示图中的解集,其中正确的是( )
2. 满足下列条件的△ABC,不是直角三角形的是( )A、∠A:∠B:∠C=5:12:13 B、a:b:c=3:4:5 C、∠C=∠A﹣∠B D、b2=a2﹣c23. 用不等式表示图中的解集,其中正确的是( ) A、x≥﹣2 B、x≤﹣2 C、x<﹣2 D、x>﹣24. 已知等腰 ,与 相邻的外角是130°,则这个三角形的顶角为( )A、65°或80° B、80° C、50° D、50°或80°5. 如图所示,在已知的 中,按以下步骤作图:①分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于两点 , ;②作直线 交 于点 ,连接 .若 , ,则 的度数为( )
A、x≥﹣2 B、x≤﹣2 C、x<﹣2 D、x>﹣24. 已知等腰 ,与 相邻的外角是130°,则这个三角形的顶角为( )A、65°或80° B、80° C、50° D、50°或80°5. 如图所示,在已知的 中,按以下步骤作图:①分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于两点 , ;②作直线 交 于点 ,连接 .若 , ,则 的度数为( )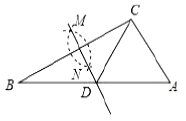 A、95° B、100° C、105° D、110°6. 不等式 的非负整数解有( )A、3个 B、4个 C、5个 D、无数个7. 为了落实精准扶贫政策,某单位针对某山区贫困村的实际情况,特向该村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5只,则多出17只母羊,若每户发放母羊7只,则有一户可分得母羊但不足3只.这批种羊共( )只.A、55 B、72 C、83 D、898. 如图甲,直角三角形 的三边a,b,c,满足 的关系.利用这个关系,探究下面的问题:如图乙, 是腰长为1的等腰直角三角形, ,延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,再延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,……,按此规律作等腰直角三角形 ( ,n为正整数),则 的长及 的面积分别是( )
A、95° B、100° C、105° D、110°6. 不等式 的非负整数解有( )A、3个 B、4个 C、5个 D、无数个7. 为了落实精准扶贫政策,某单位针对某山区贫困村的实际情况,特向该村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5只,则多出17只母羊,若每户发放母羊7只,则有一户可分得母羊但不足3只.这批种羊共( )只.A、55 B、72 C、83 D、898. 如图甲,直角三角形 的三边a,b,c,满足 的关系.利用这个关系,探究下面的问题:如图乙, 是腰长为1的等腰直角三角形, ,延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,再延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,……,按此规律作等腰直角三角形 ( ,n为正整数),则 的长及 的面积分别是( )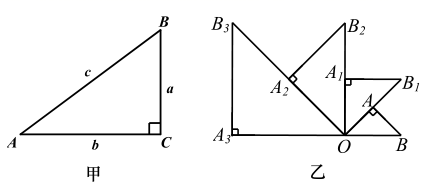 A、2, B、4, C、 , D、2,
A、2, B、4, C、 , D、2,二、填空题
-
9. “5与m的2倍的差是非负数”用不等式表示是.10. 把一个正六边形绕其中心旋转,至少旋转度,可以与自身重合.11. 在△ABC中,∠A=90°,BD平分∠ABC,AD=6厘米,BC=15厘米,则△BDC的面积为平方厘米 .
 12. 关于x的不等式组 恰好有2个整数解,则实数a的取值范围是.13. 阅读下面的材料:对于实数a,b,我们定义符号max{a,b}的意义如下:a>b时,max{a,b}=a;当a≤b时,max{a,b}=b.例如,max{2,﹣5}=2;max{3,3}=3.根据材料回答下面问题:当max{ , }= 时,x的取值范围为.
12. 关于x的不等式组 恰好有2个整数解,则实数a的取值范围是.13. 阅读下面的材料:对于实数a,b,我们定义符号max{a,b}的意义如下:a>b时,max{a,b}=a;当a≤b时,max{a,b}=b.例如,max{2,﹣5}=2;max{3,3}=3.根据材料回答下面问题:当max{ , }= 时,x的取值范围为.三、解答题
-
14. 解不等式 ,并把它的解集在数轴上表示出来.
 15. 如果点 在第二象限,那么点 关于原点的对称点 在第几象限?16. 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE.
15. 如果点 在第二象限,那么点 关于原点的对称点 在第几象限?16. 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE.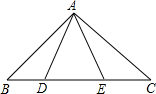 17. 解不等式组: ,并求出它的整数解.18. 如图, ,求 的各内角的度数.
17. 解不等式组: ,并求出它的整数解.18. 如图, ,求 的各内角的度数. 19. 如图,已知线段a,利用尺规作图求以a为底边、以 为高的等腰三角形
19. 如图,已知线段a,利用尺规作图求以a为底边、以 为高的等腰三角形 20. 如图,将△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上.求证:DB平分∠ADE.
20. 如图,将△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上.求证:DB平分∠ADE.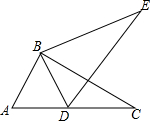 21. 如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形.
21. 如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形. 22. 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB, DF⊥AC,E、F分别是垂足.AB=AC=13,BC=10,求DE.
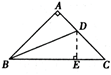
22. 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB, DF⊥AC,E、F分别是垂足.AB=AC=13,BC=10,求DE. 23. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
23. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
 (1)、求∠CBE的度数;
(1)、求∠CBE的度数;
(2)、过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
24. 某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)、求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)、如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
25. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0, -1),
⑴写出A、B两点的坐标;
⑵画出△ABC关于y轴对称的△A1B1C1 ;
⑶画出△ABC绕点C旋转180°后得到的△A2B2C2 .
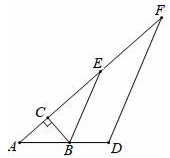
26. 在 中,若最大内角是最小内角的 倍( 为大于1的整数),则称 为 倍角三角形.例如:在 中, , , ,则称 为6倍角三角形. (1)、在 中, , ,则 为倍角三角形;(2)、若一个等腰三角形是4倍角三角形,求最小内角的度数;(3)、如图,点 在 上, 交 于点 , , , , .找出图中所有的 倍角三角形,并写出它是几倍角三角形.
(1)、在 中, , ,则 为倍角三角形;(2)、若一个等腰三角形是4倍角三角形,求最小内角的度数;(3)、如图,点 在 上, 交 于点 , , , , .找出图中所有的 倍角三角形,并写出它是几倍角三角形.