广西壮族自治区贵港市港南区2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2022-05-20 类型:期中考试
一、单选题
-
1. 在下列各数中,不是勾股数的是( )A、5,12,13 B、8, 12, 15 C、8, 15,17 D、9,40,412. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 等边三角形
B、
等边三角形
B、 平行四边形
C、
平行四边形
C、 圆
D、
圆
D、 五角星
3. 已知 中, , , ,则 的周长等于( )A、11 B、 C、12 D、134. 如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )A、九边形 B、八边形 C、七边形 D、六边形5. 如图,AD,BE,CF是△ABC的三条中线,则下列结论正确的是( )
五角星
3. 已知 中, , , ,则 的周长等于( )A、11 B、 C、12 D、134. 如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )A、九边形 B、八边形 C、七边形 D、六边形5. 如图,AD,BE,CF是△ABC的三条中线,则下列结论正确的是( ) A、 B、 C、 D、6. 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A、 B、 C、 D、6. 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )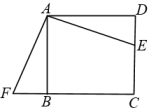 A、4 B、8 C、16 D、无法计算7. 如图, , 平分 , 交 于 , 交 于 .若 ,则 等于( )
A、4 B、8 C、16 D、无法计算7. 如图, , 平分 , 交 于 , 交 于 .若 ,则 等于( ) A、5 B、4 C、3 D、28. 两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠F=45°,∠B=60°,AC与DE交于点M.若BC∥EF,则∠DMC的大小为( )
A、5 B、4 C、3 D、28. 两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠F=45°,∠B=60°,AC与DE交于点M.若BC∥EF,则∠DMC的大小为( ) A、100° B、105° C、115° D、120°9. 如图,在△ABC中,点D、E分别是AB、AC的中点,若∠B=40°,则∠BDE的度数为( )
A、100° B、105° C、115° D、120°9. 如图,在△ABC中,点D、E分别是AB、AC的中点,若∠B=40°,则∠BDE的度数为( ) A、40° B、50° C、140° D、150°10. 如图,在 中, , , 是 的平分线, 于点 ,若 的周长等于12,则 的长是( )
A、40° B、50° C、140° D、150°10. 如图,在 中, , , 是 的平分线, 于点 ,若 的周长等于12,则 的长是( )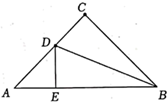 A、6 B、10 C、12 D、2411. 如图, , 是 角平分线上一点, ,垂足为 ,点 是 的中点,且 ,如果点 是射线 上一个动点,则 的最小值是( )
A、6 B、10 C、12 D、2411. 如图, , 是 角平分线上一点, ,垂足为 ,点 是 的中点,且 ,如果点 是射线 上一个动点,则 的最小值是( )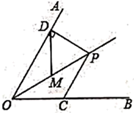 A、8 B、6 C、4 D、212. 如图所示,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④三角形BDF是直角三角形.其中正确的个数是( )
A、8 B、6 C、4 D、212. 如图所示,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④三角形BDF是直角三角形.其中正确的个数是( )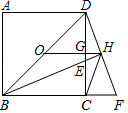 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知一个多边形的内角和是1080°,这个多边形外角和是14. 在平行四边形ABCD中,点A关于对角线的交点O的对称点 .15. 如图,在 中, ,若 ,则线段 的长为.
 16. 如图,O是直线AB上一点,已知∠1=36°,OD平分∠BOC,则∠AOD=.
16. 如图,O是直线AB上一点,已知∠1=36°,OD平分∠BOC,则∠AOD=.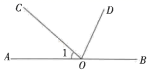 17. 一架云梯长2.5米,如图斜靠在一面墙上,梯子的底端离墙0.7米,如果梯子的顶端下滑了0.4米,那么梯子的底端在水平方向滑动了米.
17. 一架云梯长2.5米,如图斜靠在一面墙上,梯子的底端离墙0.7米,如果梯子的顶端下滑了0.4米,那么梯子的底端在水平方向滑动了米. 18. 如图,四边形ABCD为菱形, ,延长BC到E,在 内作射线CM,使得 ,过点D作 ,垂足为F.若 ,则对角线BD的长为.
18. 如图,四边形ABCD为菱形, ,延长BC到E,在 内作射线CM,使得 ,过点D作 ,垂足为F.若 ,则对角线BD的长为.
三、解答题
-
19. 如图,在▱ABCD中,∠BAD的平分线AE交DC于E,∠DAE=25°.
 (1)、求∠C、∠B的度数;(2)、若BC=5,AB=8,求CE的长.20. 如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
(1)、求∠C、∠B的度数;(2)、若BC=5,AB=8,求CE的长.20. 如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等. 21. 求图(1)(2)中x的值.
21. 求图(1)(2)中x的值. 22. 已知:如图,在▱ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
22. 已知:如图,在▱ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E. (1)、求证:四边形ACED是矩形;(2)、连接AE,若AB=2BC,求证:△ABE是等边三角形.23. 如图,在中, , D是线段AB上一点, , 连接CD, .
(1)、求证:四边形ACED是矩形;(2)、连接AE,若AB=2BC,求证:△ABE是等边三角形.23. 如图,在中, , D是线段AB上一点, , 连接CD, .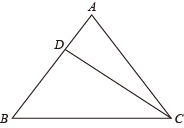 (1)、求证: .(2)、若 , 求的周长.24. 如图,在 中, 平分 , , 于点E,点F在 上, .
(1)、求证: .(2)、若 , 求的周长.24. 如图,在 中, 平分 , , 于点E,点F在 上, . (1)、求证: ;(2)、若 , ,求 的长.
(1)、求证: ;(2)、若 , ,求 的长.

