广西桂林市灌阳县2021-2022学年八年级下学期期中考试数学试卷
试卷更新日期：2022-05-20 类型：期中考试
一、单选题
-
1. Rt△ABC中，∠C=90°，∠B=40°，则∠A=（ ）A、60° B、50° C、40° D、30°2. 下列图形中既是中心对称又是轴对称的是（ ）A、
B、
C、
D、
3. 直角三角形的斜边长为10，则斜边上的中线长为（ ）A、2 B、3 C、4 D、54. 将一个四边形截去一个角后，它不可能是（ ）
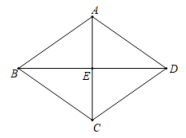
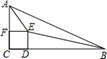
A、六边形 B、五边形 C、四边形 D、三角形5. 下列条件中，能判定一个四边形为平行四边形的是（ ）A、一组对边相等 B、一组对边平行，另一组对边相等 C、两条对角线互相垂直 D、两组对边分别相等6. 如图，Rt△ABC中，∠C=90°，∠B=30°，AD是∠BAC的平分线，AD=10，则点D到AB的距离是（ ）
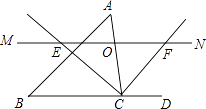
A、8 B、5 C、6 D、47. 在平行四边形ABCD中，∠A=100°，则∠C=（ ）A、80° B、90° C、100° D、120°8. 正多边形的每一个外角都等于45°，则这个多边形的边数是（ ）A、6 B、7 C、8 D、99. 如图，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=2，则OM=（ ）
A、3 B、4 C、5 D、610. 如图，P为正方形ABCD的对角线AC上任意一点，PE⊥AB于E，PF⊥BC于F，若AC＝ ，则PE+PF=（ ）
A、 B、2 C、2 D、111. 如图，在矩形ABCD中，F是BC中点，E是AD上一点，且∠ECD=30°，∠BEC=90°，EF=4cm，则矩形的面积为（ ）
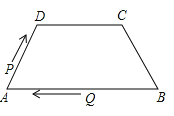
A、16cm B、 cm C、 cm D、32cm12.如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（ ）
A、4s B、3s C、2s D、1s二、填空题
-
13. 判别两个直角三角形全等的方法是.14. 若一个直角三角形的一条直角边和斜边长分别为6，10，则第三边长为.15. 在▱ABCD中，AB，BC，CD的长度分别为2x＋1，3x，x＋4，则▱ABCD的周长是.16. 在四边形ABCD中，AB=BC=CD=AD，则四边形ABCD的形状一定是.17. 在△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于D，AB=a，则DB等于.18. 如图，三个边长均为2的正方形重叠在一起，O1 ， O2是其中两个正方形的对角线交点，若把这样的n个小正方形按如图所示方式摆放，则重叠部分的面积为 ．
三、解答题
-
19. 已知△ABC的顶点A、B、C在格点上，画△ABC关于点O的中心对称图形△A1B1C1.
20. 如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且AF＝CE.求证：△ADF≌△CBE.
21. 如图，在△ABC中，∠C＝90°，∠A＝30°，点D在AC上，且∠BDC＝60°，AC＝12，求BD、BC的长.
22. 一根12米的电线杆AB，用铁丝AC、AD固定，现已知用去铁丝AC＝15米，AD＝13米，又测得地面上B、C两点之间距离是9米，B、D两点之间距离是5米，则电线杆和地面是否垂直，为什么？
23. 如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点.求证：DE BF.
