浙江省台州市玉环市2022年初中毕业升学模拟考试数学试卷(一模)
试卷更新日期:2022-05-20 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分)
-
1. 如果向东走5米记作+5米,那么-3米表示( )A、向东走5米 B、向西走5米 C、向东走3米 D、向西走3米2. 如图是某几何体的三视图,则该几何体是( )
 A、
A、 B、
B、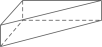 C、
C、 D、
D、 3. 自从新冠疫情爆发以来,玉环市民积极参加防疫工作并接种新冠疫苗,截至2022年3月21日,全市共计接种新冠疫苗约1740000剂次,1740000用科学记数法表示为( )A、 B、 C、 D、4. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、5. 小明在学习《实数》这一章时,用两个面积为1的正方形以如图方式拼出一个面积为2的正方形,则这个面积为2的正方形的边长的值大约在( )
3. 自从新冠疫情爆发以来,玉环市民积极参加防疫工作并接种新冠疫苗,截至2022年3月21日,全市共计接种新冠疫苗约1740000剂次,1740000用科学记数法表示为( )A、 B、 C、 D、4. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、5. 小明在学习《实数》这一章时,用两个面积为1的正方形以如图方式拼出一个面积为2的正方形,则这个面积为2的正方形的边长的值大约在( ) A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间6. 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )A、频率就是概率 B、频率与试验次数无关 C、概率是随机的,与频率无关 D、随着随机试验次数的增加,频率一般会越来越接近概率7. 如图,在 中, ,观察尺规作图的痕迹,则 的度数为( )
A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间6. 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )A、频率就是概率 B、频率与试验次数无关 C、概率是随机的,与频率无关 D、随着随机试验次数的增加,频率一般会越来越接近概率7. 如图,在 中, ,观察尺规作图的痕迹,则 的度数为( ) A、 B、 C、 D、8. 如图,面积为18的正方形 内接于 ,则弧 的长度为( )
A、 B、 C、 D、8. 如图,面积为18的正方形 内接于 ,则弧 的长度为( ) A、 B、 C、 D、9. 小明和小亮期中考试的语文、数学成绩分别都是80分,m分.到了期末考时,小明期末考试的语文、数学两科成绩依次比期中考试增长了20%,10%两科总成绩比期中增长的百分数为a.小亮期末考试的语文、数学两科成绩依次比期中考试增长了15%,10%两科总成绩比期中增长的百分数为b,则( )A、 B、 C、 D、10. 如图,在菱形 中, 的两顶点 分别落在边 上,从给出的四个条件中任选一个:① ;② ;③ ;④ .能够推出 为等边三角形的有( )
A、 B、 C、 D、9. 小明和小亮期中考试的语文、数学成绩分别都是80分,m分.到了期末考时,小明期末考试的语文、数学两科成绩依次比期中考试增长了20%,10%两科总成绩比期中增长的百分数为a.小亮期末考试的语文、数学两科成绩依次比期中考试增长了15%,10%两科总成绩比期中增长的百分数为b,则( )A、 B、 C、 D、10. 如图,在菱形 中, 的两顶点 分别落在边 上,从给出的四个条件中任选一个:① ;② ;③ ;④ .能够推出 为等边三角形的有( ) A、①② B、②④ C、①②④ D、①③④
A、①② B、②④ C、①②④ D、①③④二、填空题(本题有6小题,每小题5分,共30分)
-
11. 因式分解:x2+3x =12. 如图,直线 ,将一块含 角的直角三角板 按如图方式放置 ,其中一条直角边的两顶点 分别落在直线 上,若 ,则 度.
 13. 一个不透明的布袋中有1个红球,2个黑球,这些球除颜色外无其他差别.先随机摸出一个小球,记下颜色后放回搅匀再摸出一个小球,则两次摸出的小球颜色相同的概率是 .14. 如图,反比例函数 的图象经过点 ,则当函数值 时,自变量x的取值范围为 .
13. 一个不透明的布袋中有1个红球,2个黑球,这些球除颜色外无其他差别.先随机摸出一个小球,记下颜色后放回搅匀再摸出一个小球,则两次摸出的小球颜色相同的概率是 .14. 如图,反比例函数 的图象经过点 ,则当函数值 时,自变量x的取值范围为 . 15. 如图,已知 内切于 边上切点为点D,作 的直径 ,连结 并延长 交 于点F,若 ,则 的长为 .
15. 如图,已知 内切于 边上切点为点D,作 的直径 ,连结 并延长 交 于点F,若 ,则 的长为 . 16. 斜抛小球,小球触地后呈抛物线反弹,每次反弹后保持相同的抛物线形状(开口方向与开口大小前后一致),第一次反弹后的最大高度为 ,第二次反弹后的最大高度为 ,第二次反弹后,小球越过最高点落在垂直于地面的挡板C处,且离地高度 ,若 ,则 为 .
16. 斜抛小球,小球触地后呈抛物线反弹,每次反弹后保持相同的抛物线形状(开口方向与开口大小前后一致),第一次反弹后的最大高度为 ,第二次反弹后的最大高度为 ,第二次反弹后,小球越过最高点落在垂直于地面的挡板C处,且离地高度 ,若 ,则 为 .
三、解答题(本题有8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分)
-
17. 计算: .18. 解方程: .19. 大跳台滑雪比赛的某段赛道如图所示,中国选手谷爱凌从离水平地面100米高的A点出发( 米),沿俯角为 的方向先滑行140米到达D点,然后再沿俯角为 的方向滑行到地面的C处,求她滑行的水平距离 约为多少米.(结果精确到0.1米,参考数据: )
 20. 桌面上有甲、乙、丙三个杯子,三个杯子内原本均装有一些水,先将甲杯的水全部倒入丙杯,此时丙杯的水量为原本甲杯内水量的3倍;再将乙杯的水全部倒入丙杯,此时丙杯的水量为原本乙杯内水量的4倍少150毫升.若过程中水没有溢出,则原本甲、乙两杯内的水量相差多少毫升?
20. 桌面上有甲、乙、丙三个杯子,三个杯子内原本均装有一些水,先将甲杯的水全部倒入丙杯,此时丙杯的水量为原本甲杯内水量的3倍;再将乙杯的水全部倒入丙杯,此时丙杯的水量为原本乙杯内水量的4倍少150毫升.若过程中水没有溢出,则原本甲、乙两杯内的水量相差多少毫升? 21. 如图,在矩形 中,O是对角线 的中点,过点O作 分别交 于点 .
21. 如图,在矩形 中,O是对角线 的中点,过点O作 分别交 于点 . (1)、求证: ;(2)、若 ,求 的长.22. 2月20日,北京冬奥会圆满落幕,在无与伦比的盛会背后,有着许多志愿者的辛勤付出.在志愿者招募之时,甲、乙两所大学积极开展了志愿者选拔活动,现从两所大学参加测试的志愿者中分别随机抽取了10名志愿者的测试成绩进行整理和分析(成绩得分用x表示,共分成四组:A. ,B. ,C. ,D. ),下面给出了部分信息:
(1)、求证: ;(2)、若 ,求 的长.22. 2月20日,北京冬奥会圆满落幕,在无与伦比的盛会背后,有着许多志愿者的辛勤付出.在志愿者招募之时,甲、乙两所大学积极开展了志愿者选拔活动,现从两所大学参加测试的志愿者中分别随机抽取了10名志愿者的测试成绩进行整理和分析(成绩得分用x表示,共分成四组:A. ,B. ,C. ,D. ),下面给出了部分信息:甲校10名志愿者的成绩(分)为: .
乙校10名志愿者的成绩分布如扇形图所示,其中在C组中的数据为: .
甲、乙校抽取的志愿者成绩统计表
甲校
乙校
平均数
87
87
中位数
87.5
b
方差
79.4
众数
c
95
 (1)、由上表填空: , , ;(2)、你认为哪个学校的志愿者测试成绩的总体水平较好?请至少写出两条理由;(3)、若甲校参加测试的志愿者有200名,请估计甲校成绩在90分及以上的约有多少人.23. 面朝大海,春暖花开!榴岛大地正值草莓上市销售的旺季.某商家以每盒20元的价格购进一批盒装草莓,经市场调查发现:在一段时间内,草莓的日销售量y(盒)与每盒售价x(元)满足一次函数关系,其图象如下图所示:
(1)、由上表填空: , , ;(2)、你认为哪个学校的志愿者测试成绩的总体水平较好?请至少写出两条理由;(3)、若甲校参加测试的志愿者有200名,请估计甲校成绩在90分及以上的约有多少人.23. 面朝大海,春暖花开!榴岛大地正值草莓上市销售的旺季.某商家以每盒20元的价格购进一批盒装草莓,经市场调查发现:在一段时间内,草莓的日销售量y(盒)与每盒售价x(元)满足一次函数关系,其图象如下图所示: (1)、求y关于x的函数关系式;(2)、根据市场的定价规则,草莓的售价每盒不得高于49元,当售价定为多少时,日销售利润最大?最大利润是多少?(3)、为了增加店铺的人气,商家决定搞促销活动,顾客每购买一盒草莓可以获得a元的现金奖励 ,商家想在日销售量不少于40盒的基础上,使日销售最大利润为1568元,求此时a的值.24. 如图, 为等边三角形,D为边 上一动点,在 上方作等边 交 于点F,连结 .
(1)、求y关于x的函数关系式;(2)、根据市场的定价规则,草莓的售价每盒不得高于49元,当售价定为多少时,日销售利润最大?最大利润是多少?(3)、为了增加店铺的人气,商家决定搞促销活动,顾客每购买一盒草莓可以获得a元的现金奖励 ,商家想在日销售量不少于40盒的基础上,使日销售最大利润为1568元,求此时a的值.24. 如图, 为等边三角形,D为边 上一动点,在 上方作等边 交 于点F,连结 . (1)、求证: AE∥BC ;(2)、①当D为 中点时, ▲ ;
(1)、求证: AE∥BC ;(2)、①当D为 中点时, ▲ ;②当 时,求 的值;(用含k的式子表示)
(3)、过点D作 于H,交 于G,若 ,且点G为 中点,求k的值.