浙江省金华市义乌市2021-2022学年九年级下学期期中数学试题（一模）

试卷更新日期：2022-05-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，比﹣2小的数是（）

A、3 B、1 C、﹣1 D、﹣3

查看试题解析
2. 为应对疫情，许多企业跨界抗疫，生产口罩截至2月29日，全国口罩日产量达到116000000只．将116000000用科学记数法表示应为（）

A、11.6×10⁷ B、1.16×10⁷ C、1.16×10⁸ D、1.16×10⁹

查看试题解析
3. 下列计算正确的是（）

A、3a＋4b＝7ab B、(ab³)³＝ab⁶ C、(a＋2)²＝a²＋4 D、x¹²÷x⁶＝x⁶

查看试题解析
4. 在一个不透明的口袋中装有若干个只有颜色不同的白球和黄球，如果袋中黄球的个数是白球的两倍，那么摸到白球的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、不能确定

查看试题解析
5. 如图，∠BAC＝36°，点O在边AB上，⊙O与边AC相切于点D，交边AB于点E，F，连接FD，则∠AFD等于（）

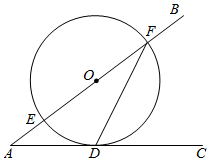A、27° B、29° C、35° D、37°

查看试题解析
6. 如图，小树AB在路灯O的照射下形成投影BC．若树高AB=2m，树影BC=3m，树与路灯的水平距离BP=4.5m．则路灯的高度OP为（）

A、3m B、4m C、4.5m D、5m

查看试题解析
7. 如图，已知点O是矩形ABCD的对称中心，且AB＞AD.点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF的形状不可能是（）

A、平行四边形 B、菱形 C、矩形 D、正方形

查看试题解析
8. 若二次函数y＝kx²﹣2x﹣1与x轴有交点，则k的取值范围是（）

A、k＞﹣1 B、k≤1且k≠0 C、k＜﹣1 D、k≥﹣1且k≠0

查看试题解析
9. 如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线l上取一点P，使，使∠APB=30°，则满足条件的点P共有（）

A、l个 B、2个 C、3个 D、无数个

查看试题解析
10. 如图，正方形 $A B C D$ 边长为4，点 $E$ 在边 $D C$ 上运动（不含端点），以 $A E$ 为边作等腰直角三角形 $A E F$ ， ∠AEF＝90°，连接 $D F$ .下面四个说法中有几个正确（）
①当 $D E = 1$ 时， $A F = \sqrt{34}$ ；②当 $D E = 2$ 时，点 $B$ ， $D$ ， $F$ 共线；③当三角形 $A D F$ 与三角形 $E D F$ 面积相等时，则DE＝ $2 \sqrt{5} - 2$ ；④当 $A D$ 平分∠EAF时，则DE＝ $4 \sqrt{2} - 3$

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解：2a²﹣8= ．

查看试题解析
12. 半径为10cm，母线长为15cm的圆锥的侧面积为.

查看试题解析
13. 为了考察甲、乙两块地小麦的长势，抽样测得小麦株苗的方差分别为S_甲²＝3.6，S_乙²＝15.8，则地的小麦长势更整齐．(填“甲”或“乙”)

查看试题解析
14. 如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S△PAB＝ $\frac{1}{3}$ S矩形ABCD，则点P到A、B两点距离之和PA+PB的最小值为.

查看试题解析
15. 如图，点A是射线y═ $\frac{5}{4} x$ （x≥0）上一点，过点A作AB⊥x轴于点B，以AB为边在其右侧作正方形ABCD，过点A的双曲线y＝ $\frac{k}{x}$ 交CD边于点E，则 $\frac{D E}{E C}$ 的值为

查看试题解析
16. 如图，点A，B是直线AB上的固定的两点，AB＝5．点M是平面内一动点，满足 $\frac{M B}{M A} = \frac{2}{3}$ ．

(1)、当△ABM为等腰三角形时，△ABM的周长为．

(2)、当△ABM的面积最大时，AM＝

查看试题解析

三、解答题

17.

(1)、 $\sqrt{18}$ + $| - \sqrt{2} |$ -（2012﹣π）⁰-4sin45°

(2)、解方程：x²-10x＋9＝0．

查看试题解析
18. 如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点都在小方格的顶点上．现以点D，E，F，G，H中的三个点为顶点画三角形．

(1)、在图甲中画出一个三角形与△ABC相似且相似比为1：2．

(2)、在图乙中画出一个三角形与△ABC的面积比为1：4但不相似．

查看试题解析

19. 为了从甲、乙两位同学中选拔一人参加知识竞赛，举行了6次选拔赛，根据两位同学6次选拔赛的成绩，分别绘制了如图统计图．

(1)、填写下列表格

	平均数/分	中位数/分	众数/分
甲	90	①	93
乙	②	87.5	③

(2)、如果分别从甲、乙两人的6次成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都不低于90分的概率．

查看试题解析

20. 图（1）为某大型商场的自动扶梯．图（2）中的AB为从一楼到二楼的扶梯的侧面示意图．小明站在扶梯起点A处时，测得天花板上日光灯C的仰角为37°，此时他的眼睛D与地面的距离AD＝1.8m，之后他沿一楼扶梯到达顶端B后又沿BL（ $B L ∥ M N$ ）向正前方走了2m，发现日光灯C刚好在他的正上方．已知自动扶梯AB的坡度为1：2.4，AB的长度是13m，（参考数据：sin37°≈0.6，cos37°＝0.8，tan37°≈0.75）．

(1)、求图中B到一楼地面的高度．

(2)、求日光灯C到一楼地面的高度．（结果精确到十分位）．

查看试题解析
21. 如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点P，PD⊥AC于点D.

(1)、求证：PD是⊙O的切线；

(2)、若∠CAB=120°，AB=6，求BC的长.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = x^{2} + (a - 1) x - 2 a$ ，其中a为常数，点 $A (- 4 ， 2 a - 4)$ 在此抛物线上．

(1)、求此时抛物线的解析式及点A的坐标；

(2)、设点 $M (x ， y)$ 为抛物线上一点，当 $- 3 \leq x \leq 2$ 时，求纵坐标y的最大值与最小值的差；

(3)、已知点 $P (- 2 ， - 3) ， Q (2 ， - 3)$ 为平面直角坐标系内两点，连接 $P Q$ ．若抛物线向上平移c个单位 $(c > 0)$ 的过程中，与线段 $P Q$ 恰好只有一个公共点，请直接写出c的取值范围．

查看试题解析
23. 我们定义：对角线互相垂直的四边形叫做“对垂四边形”．

(1)、如图1，四边形ABCD为“对垂四边形”．求证：AB²+CD²＝BC²+AD² ．

(2)、如图2，E是四边形ABCD内一点，连结AE，BE，CE和DE，AC与BD交于点O．若∠BEC＝90°，∠BAC＝∠BDC，∠1+∠2＝∠3．求证：四边形ABCD为“对垂四边形”．

(3)、如图3，四边形ABCD为“对垂四边形”，AB＝AC，∠ADC＝120°，AD＝3，BC＝ $\sqrt{5}$ DC，求CD的长．

查看试题解析
24. 如图1，在矩形ABCD中，AB＝8，AD＝6，动点P沿着边AB从点A运动到点B，同时动点Q沿着边BC，CD从点B运动到点D，它们同时到达终点，BD与PQ交于点E．若记点Q的运动路程为x，线段BP的长记为y．

(1)、求y关于x的函数表达式．

(2)、如图2，当点Q在CD上时，求 $\frac{B E}{D E}$ ．

(3)、将矩形沿着PQ折叠，点B的对应点为点F，连结EF，当EF所在直线与△BCD的一边垂直时，求BP的长．

查看试题解析