2021-2022学年初中数学北师大版七年级下学期期末复习试卷 第一章整式的乘除
试卷更新日期:2022-05-19 类型:复习试卷
一、单选题
-
1. 的计算结果是( )A、 B、 C、 D、2. 下列计算错误的是( )A、 B、 C、 D、3. 若满足关系式 , 则代数式( )A、-1 B、0 C、 D、14. 石墨烯是现在世界上最薄的纳米材料,其理论厍度应是0.0000098m,用科学记数法表示0.0000098是( )A、0.98×10﹣5 B、9.8×105 C、9.8×10﹣6 D、9.8×10﹣55. 新冠病毒的直径为0.000000125米,这个数据用科学记数法表示为( )A、 B、 C、 D、6. 下列结论中: ①若 , 则 ;②若 , 则 的值为 ; ③若规定: 当 时, , 若 , 则 ;④若 , 则 可表示为 ; ⑤若 的运算结果中不含 的一次项, 则 . 其中正确的个数是 ( )A、5 B、4 C、3 D、27. 如图,在长方形 中放入一个边长为8的大正方形 和两个边长为6的小正方形(正方形 和正方形 ).3个阴影部分的面积满足 ,则长方形 的面积为( )
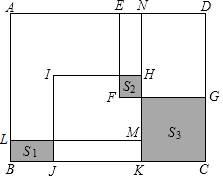 A、90 B、96 C、98 D、1008. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A、90 B、96 C、98 D、1008. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )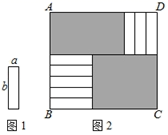 A、 B、 C、 D、9. 记 ,则 ( )A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方10. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、
A、 B、 C、 D、9. 记 ,则 ( )A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方10. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、二、填空题
-
11. 计算 .12. 计算:= , =13. 把式子化简的结果是.14. 计算15. 若 , , , 为正数),则 .16. 嘉嘉同学动手剪了如图1所示的正方形与矩形纸片若干张.
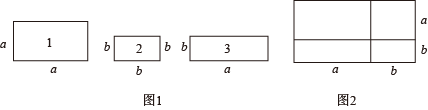 (1)、他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图2).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 .(2)、如果要拼成一个长为 , 宽为的大长方形,则需要3号卡片张.17. 数学活动课上,小明同学尝试将正方形纸片剪去一个小正方形,剩余部分沿虚线剪开,拼成新的图形。现给出下列3种不同的剪、拼方案,其中能够验证平方差公式的方案是 。(请填上正确的序号)
(1)、他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图2).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 .(2)、如果要拼成一个长为 , 宽为的大长方形,则需要3号卡片张.17. 数学活动课上,小明同学尝试将正方形纸片剪去一个小正方形,剩余部分沿虚线剪开,拼成新的图形。现给出下列3种不同的剪、拼方案,其中能够验证平方差公式的方案是 。(请填上正确的序号)
三、计算题
-
18. 用简便方法计算下列各题:(1)、;(2)、 .19. 计算:(1)、;(2)、 .20.(1)、若 ,求 , 的值;(2)、若 , ,求 , .
四、综合题
-
21. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了 为正整数)的展开式(按 的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应 展开式中的系数.
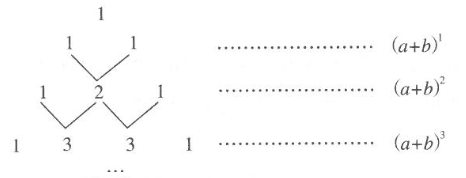 (1)、根据上面的规律,写出 的展开式;(2)、利用上面的规律计算: .22.
(1)、根据上面的规律,写出 的展开式;(2)、利用上面的规律计算: .22.小刚同学动手剪了如图①所示的正方形与长方形纸片若干张.观察与操作:
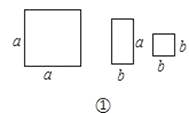
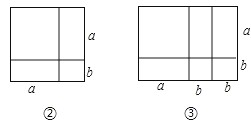
(1)他拼成如图②所示的正方形,根据四个小纸片的面积之和等于大正方形的面积,得到:a2+2ab+b2=(a+b)2 , 验证了完全平方公式;即:多项式 a2+2ab+b2分解因式后,其结果表示正方形的长(a+b)与宽(a+b)两个整式的积.
(2)当他拼成如图③所示的矩形,由面积相等又得到:a2+3ab+2b2=(a+2b)(a+b),即:多项式 a2+3ab+2b2分解因式后,其结果表示矩形的长(a+2b)与宽(a+b)两个整式的积.
问题解决:
(1)请你依照小刚的方法,利用拼图写出恒等式a2+4ab+3b2 . (画图说明,并写出其结果)
(2)试猜想面积是2a2+5ab+3b2的矩形,其长与宽分别是多少?(画图说明,并写出其结果)23.(1)、【知识情境】通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
如图1,在边长为a的正方形中挖掉一个边长为b的小正方形 (a>b) .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是;
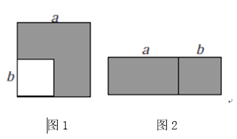 (2)、【拓展探究】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
(2)、【拓展探究】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.如图3是边长为 的正方体,被如图所示的分割线分成8块.
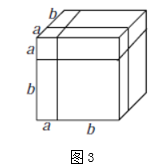
用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
;
(3)、已知 , ,利用上面的恒等式求 的值.24.(1)、已知4m=a,8n=b,用含a,b的式子表示下列代数式:①求:22m+3n的值.
②求:22m-6n的值.
(2)、已知2×8x×16=223 , 求x的值.25. 图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.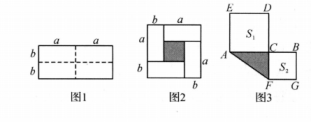 (1)、观察图2,请你写出下列三个代数式(a+b)2 , (a-b)2 , ab之间的等量关系为 .(2)、运用你所得到的公式,计算:若m,n为实数,且mn=-3,m-n=4,试求m+n的值.(3)、如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=23,求图中阴影部分面积.26. 如图1,边长为 的大正方形有一个边长为 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)
(1)、观察图2,请你写出下列三个代数式(a+b)2 , (a-b)2 , ab之间的等量关系为 .(2)、运用你所得到的公式,计算:若m,n为实数,且mn=-3,m-n=4,试求m+n的值.(3)、如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=23,求图中阴影部分面积.26. 如图1,边长为 的大正方形有一个边长为 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)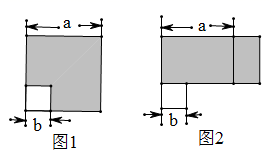 (1)、如图1,可以求出阴影部分的面积是(写成平方差的形式)(2)、如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是.(写成多项式乘法形式)(3)、比较左、右两图的阴影部分面积,可以得到公式.(4)、请应用这个公式完成下列各题:
(1)、如图1,可以求出阴影部分的面积是(写成平方差的形式)(2)、如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是.(写成多项式乘法形式)(3)、比较左、右两图的阴影部分面积,可以得到公式.(4)、请应用这个公式完成下列各题:①已知 , ,则
②计算: =
③计算:
27. 用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为 , 的正方形和长为 宽为 的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为: .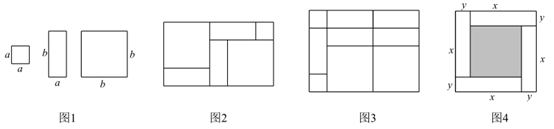 (1)、图3可以解释为等式:;(2)、要拼出一个两边长为 , 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论;
(1)、图3可以解释为等式:;(2)、要拼出一个两边长为 , 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论; 块,
块,  块,
块,  块(3)、如图4,大正方形的边长为 ,小正方形的边长为 ,若用 , ( )表示四个相同小长方形的两边长,以下关系式正确的是 (填序号).① ;② ;③ ;④ .
块(3)、如图4,大正方形的边长为 ,小正方形的边长为 ,若用 , ( )表示四个相同小长方形的两边长,以下关系式正确的是 (填序号).① ;② ;③ ;④ .