北师大版2022年中考数学模拟试卷二(5月份)
试卷更新日期:2022-05-18 类型:中考模拟
一、单选题
-
1. 下列说法正确的是( )A、三角形可分为钝角三角形、等腰三角形、锐角三角形 B、等边三角形是特殊的等腰三角形 C、等腰三角形是特殊的等边三角形 D、所有的等腰三角形都是锐角三角形2. 的相反数是( )A、1 B、-1 C、2021 D、-20213. 如图,在△ABC中,∠A=50°,OB平分∠ABC,OC平分∠ACB,则∠BOC的度数为( )
 A、65° B、70° C、115° D、125°4. 老师:若实数 , , 在数轴上对应点的位置如图所示,学生1:;学生2:;学生3:;学生4: . 老师:只有1名学生的结论是正确的.这名学生是( )
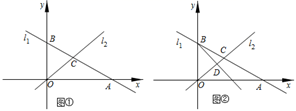
A、65° B、70° C、115° D、125°4. 老师:若实数 , , 在数轴上对应点的位置如图所示,学生1:;学生2:;学生3:;学生4: . 老师:只有1名学生的结论是正确的.这名学生是( )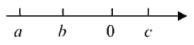 A、学生1 B、学生2 C、学生3 D、学生45. 如图,AB 为⊙O 的直径,点 C 是 AB 上方半圆上的一点,点 D 是 AB 下方半圆的中点,连接 AC,BC,AD,过点 D 作 DE∥AB 交 CB 的延长线于点 E.若 AD= 5 ,则 AC·CE的最大值为( )
A、学生1 B、学生2 C、学生3 D、学生45. 如图,AB 为⊙O 的直径,点 C 是 AB 上方半圆上的一点,点 D 是 AB 下方半圆的中点,连接 AC,BC,AD,过点 D 作 DE∥AB 交 CB 的延长线于点 E.若 AD= 5 ,则 AC·CE的最大值为( ) A、50 B、50 C、100 D、756. 根据下列表述,不能确定具体位置的是( )A、电影院一层的3排4座 B、太原市解放路85号 C、南偏西 D、东经 ,北纬7. 如图,正方形的边长为 ,图中阴影部分的面积可以表示为( )
A、50 B、50 C、100 D、756. 根据下列表述,不能确定具体位置的是( )A、电影院一层的3排4座 B、太原市解放路85号 C、南偏西 D、东经 ,北纬7. 如图,正方形的边长为 ,图中阴影部分的面积可以表示为( ) A、 B、 C、 D、8. 如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( )
A、 B、 C、 D、8. 如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( ) A、16 B、24 C、32 D、409. 如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致是( )
A、16 B、24 C、32 D、409. 如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致是( )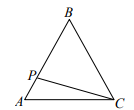 A、
A、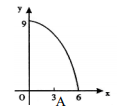 B、
B、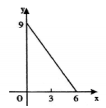 C、
C、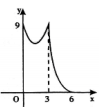 D、
D、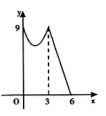 10. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
10. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )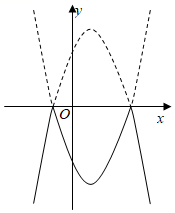 A、 或﹣2 B、 或﹣2 C、 或﹣3 D、 或﹣3
A、 或﹣2 B、 或﹣2 C、 或﹣3 D、 或﹣3二、填空题
-
11. 若方程x2﹣4x+3=0的两根是等腰三角形的底和腰,则它的周长为 .12. 计算:( ﹣1)0+(﹣ )﹣2=.13. 王老师把几本《数学大世界》给学生们阅读.若每人3本,则剩下3本;若每人5本,则有一位同学分不到书看,只够平均分给其他几位同学.则学生与书本的数量分别是;14. 用火柴棒按如图在方式搭图形,搭第n个图形需 根火柴棒.
 15. 已知O、A、B的坐标分别是 , 在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为.16. 如图,把面积为5的正方形ABCD放到数轴上,使得正方形的一个顶点A与 重合,那么顶点B在数轴上表示的数是 .
15. 已知O、A、B的坐标分别是 , 在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为.16. 如图,把面积为5的正方形ABCD放到数轴上,使得正方形的一个顶点A与 重合,那么顶点B在数轴上表示的数是 . 17. 二次函数 的图象如图所示,以下结论:① ;② ;③ ;④其顶点坐标为 ;⑤当 时, 随 的增大而减小;⑥ 中,正确的有(只填序号)
17. 二次函数 的图象如图所示,以下结论:① ;② ;③ ;④其顶点坐标为 ;⑤当 时, 随 的增大而减小;⑥ 中,正确的有(只填序号) 18. 今年春节某超市组装了甲、乙两种礼品盆,他们都是由 三种零食组成,其中甲礼品盒装有3千克 零食,1千克 零食,1千克 零食,乙礼品盒装有2千克 零食,2千克 零食,2千克 零食,甲、乙两种礼品盒的成本均为盆中 三种零食的成本之和.已知每千克 的成本为10元,乙种礼品盒的售价为60元,每盒利润率为25%甲种每盒的利润率为50%当甲、乙两种礼盒的销售利润率为 时,该商场销售甲、乙两种礼盒的数量之比是.
18. 今年春节某超市组装了甲、乙两种礼品盆,他们都是由 三种零食组成,其中甲礼品盒装有3千克 零食,1千克 零食,1千克 零食,乙礼品盒装有2千克 零食,2千克 零食,2千克 零食,甲、乙两种礼品盒的成本均为盆中 三种零食的成本之和.已知每千克 的成本为10元,乙种礼品盒的售价为60元,每盒利润率为25%甲种每盒的利润率为50%当甲、乙两种礼盒的销售利润率为 时,该商场销售甲、乙两种礼盒的数量之比是.三、解答题
-
19.(1)、化简: .(2)、解不等式组: .20. 先化简后求值: ,其中 , .21. 如图,甲、乙两个完全相同的转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,记下甲、乙两个转盘中指针所指的数字.请用画树状图或列表的方法,求这两个数字之和为偶数的概率.
 22. 动物园在检测成年麦哲伦企鹅的身体状况时,最重要的一项工作就是称体重,已知某动物园对6只成年麦哲伦企鹅进行称重检测,以4千克为标准,超过或不足的千克数分别用正数和负数表示,称重记录如下表所示,求这6只企鹅的总体重
22. 动物园在检测成年麦哲伦企鹅的身体状况时,最重要的一项工作就是称体重,已知某动物园对6只成年麦哲伦企鹅进行称重检测,以4千克为标准,超过或不足的千克数分别用正数和负数表示,称重记录如下表所示,求这6只企鹅的总体重
编号
1
2
3
4
5
6
差值(kg)
-0.08
+0.09
+0.05
-0.05
+0.08
+0.06
23. 图1,图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图,已知运动员的小腿 与斜坡 垂直,大腿 与斜坡 平行,且 三点共线,若雪仗 长为 , , ,求此刻运动员头部 到斜坡 的高度 (精确到 )(参考数据: )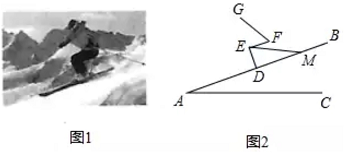 24. 如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
24. 如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF. 25. 如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使三角形ABC的面积为1,写出所有符合条件的表示点C的有序数对.
25. 如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使三角形ABC的面积为1,写出所有符合条件的表示点C的有序数对. 26. 请在横线上填写结论或推理依据:
26. 请在横线上填写结论或推理依据:
已知: , 平分 , 平分 .
求证: .
证明:
∴ ▲ ,( ▲ )
平分
( ▲ )
同理
∴ ▲
( ▲ )