北师大版2022年中考数学模拟试卷一（5月份）

试卷更新日期：2022-05-18 类型：中考模拟

进入出卷网下载

一、单选题

1. “新冠病毒”的英语“NewCoronavirus”中，字母“o”出现的频率是（）.

A、 $\frac{2}{11}$ B、1 C、2 D、 $\frac{1}{7}$

查看试题解析
2. 函数y= $\sqrt{1 - x}$ 中，自变量x的取值范围在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图所示，直线a∥b， $∠ 2 = 28 °$ ， $∠ 1 = 50 °$ ，则 $∠ A =$ （）

A、32︒ B、78︒ C、22︒ D、20︒

查看试题解析
4. 已知点 $A (m - 1 ， m + 6)$ 在 $y$ 轴上，则 $m =$ （）

A、 $- 6$ B、6 C、 $- 1$ D、1

查看试题解析
5. 有理数 $a$ 、 $b$ 、 $c$ 、 $d$ 在数轴上对应的点的位置如图所示，则下列结论错误的是（）

A、 $| d | > 3$ B、 $b c < 0$ C、 $b + d > 0$ D、 $| c - a | + c = a$

查看试题解析
6. 用配方法解方程 $x^{2} + 4 x - 7 = 0$ ，变形后的结果正确的是（）

A、 ${(x + 2)}^{2} = - 11$ B、 ${(x + 2)}^{2} = 11$ C、 ${(x + 2)}^{2} = 7$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
7. 已知：a＝ $\frac{1}{2 - \sqrt{3}}$ ，b＝ $\frac{1}{2 + \sqrt{3}}$ ，则a与b的关系是（）

A、a－b＝0 B、a＋b＝0 C、ab＝1 D、a²＝b²

查看试题解析
8. 如图，为了测量池塘边A、B两地之间的距离，在线段AB的同侧取一点C，连接CA并延长至点D，连接CB并延长至点E，使得A、B分别是CD、CE的中点，若DE＝16m，则AB的长度是（）

A、8m B、9m C、12m D、6m

查看试题解析
9. 如图，平行四边形 $O A B C$ 的顶A在x轴的正半轴上，点 $D (3 ， 2)$ 在对角线 $O B$ 上，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图像经过C、D两点．已知平行四边形 $O A B C$ 的面积是 $\frac{15}{2}$ ，则点B的坐标为（）

A、 $(4 ， \frac{8}{3})$ B、 $(\frac{9}{2} ， 3)$ C、 $(5 ， \frac{10}{3})$ D、 $(\frac{24}{5} ， \frac{16}{5})$

查看试题解析
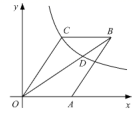10. 如图，点A ， B ， C ， D ， E为⊙O的五等分点，动点M从圆心O出发，沿线段OA→劣弧AC→线段CO的路线做匀速运动，设运动的时间为t ， ∠DME的度数为y ，则下列图象中表示y与t之间函数关系最恰当的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 某种药品的说明书上标明保存温度是（20±2）℃，请你写出一个适合药品保存的温度．

查看试题解析
12. 若一元二次方程x²－2x－3a=0无实根，则a取值范围是.

查看试题解析
13. 比较大小： $- 2 \sqrt{5}$ $- 3 \sqrt{2}$ ．

查看试题解析
14. 如图，在 $△ A B C$ 中，分别以点 $A$ 和点 $B$ 为圆心，大于 $\frac{1}{2} A B$ 为半径画弧，两弧相交于点 $M$ 、 $N$ ，作直线 $M N$ ，交 $B C$ 于点 $D$ ， $△ A D C$ 的周长为15， $A B = 7$ ，则 $△ A B C$ 的周长为.

查看试题解析
15. 某登山队从大本营出发，在向上攀登的过程中，测得所在位置的气温y℃与向上攀登的高度xkm的几组对应值如表：

向上攀登的高度x/km

0.5

1.0

1.5

2.0

气温y/℃

2.0

﹣1.0

﹣4.0

﹣7.0

若每向上攀登1km，所在位置的气温下降幅度基本一致，则向上攀登的海拔高度为2.3km时，登山队所在位置的气温约为℃．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B C = 4$ ，面积是10， $A C$ 的垂直平分线 $E F$ 分别交 $A C$ ， $A B$ 边于E，F点，若点D为 $B C$ 边的中点，点M为线段 $E F$ 上一动点，则 $△ C D M$ 周长的最小值为．

查看试题解析
17. 如图，在正方形ABCD中，AB＝4，点E是BC上的一个动点，将△CDE绕着点E逆时针旋转90°，得到△C′D′E，则A，D′两点距离的最小值等于.

查看试题解析
18. 菱形 $A B C D$ 边 $A B$ 、 $A D$ 上分别有E、F两点， $B E = D F$ ，连接 $C E$ ， $∠ B E C = ∠ F E C$ ，若 $\tan ∠ E C D = 2$ ， $C D = 5$ ，则菱形 $A B C D$ 的面积是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{8} \times \sqrt{\frac{1}{2}} - 2 s i n 60 ° - \frac{2}{\sqrt{3} + 1} + (2 \sqrt{3} - π)^{0}$

(2)、（π- $\sqrt{10}$ ）⁰+| $\sqrt{2}$ -1|+（ $\frac{1}{2}$ ）^-1-2sin45°．

查看试题解析
20. 先化简，再求值： $(2 m + 3) \cdot (2 m - 3) - {(m - 1)}^{2} + {(2 m)}^{3} \div (- 8 m)$ ，其中 $m$ 满足 $m^{2} + m - 2 = 0.$

查看试题解析
21. 据《重庆晨报》，2007年，重庆市被国家评为无偿献血先进城市，医疗临床用血实现了100%来自市民自愿献血，无偿献血总量6.5吨，居全国第三位．现有小莉，小罗，小强三个自愿献血者，两人血型为O型，一人血型为A型．若在三人中随意挑选一人献血，两年以后又从此三人中随意挑选一人献血，试求两次所抽血的血型均为O型的概率．（要求：用列表或画树状图的方法解答）

查看试题解析
22. 某校为了解八年级学生参加社会实践活动情况，随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：

（Ⅰ）本次接受随机抽样调查的学生人数为 ▲ ，图①中的m的值为 ▲ ；

（Ⅱ）求本次抽样调查获取的样本数据的众数、中位数和平均数；

（Ⅲ）若该校八年级学生有240人，估计参加社会实践活动时间大于7天的学生人数．

查看试题解析
23. 已知∠BAC=∠DAE，∠1=∠2，BD=CE，问△ABD≌△ACE吗？为什么？

查看试题解析
24. 如图，某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度，他们先在A处测得古塔顶端点D的仰角为45°，再沿着BA的方向后退20m至C处，测得古塔顶端点D的仰角为30°.求该古塔BD的高度（ $\sqrt{3} \approx 1.732$ ，结果保留一位小数）.

查看试题解析
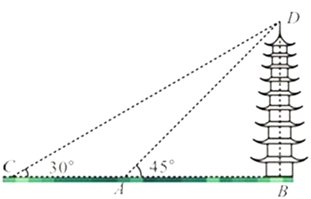25. 如图，在 △ ABC中，BD是∠ABC的平分线，CD是外角∠ACE的平分线．
求证：∠D= $\frac{1}{2}$ ∠A．

查看试题解析
26. 如图，△ABC中，BD、CE是△ABC的两条高，点F、M分别是DE、BC的中点．求证：FM⊥DE。

查看试题解析
27. 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开.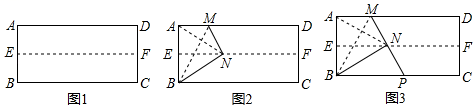
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN.连结AN，易知△ABN的形状是 ▲ .
论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由.

查看试题解析
28. 如图，在△ABC中，BC=7cm，AC=24cm，AB=25cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2 cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5 cm/s.若点P，Q分别从B，C同时运动，请解答下面的问题：

(1)、经过多少时间后，P，Q两点间的距离为 $5 \sqrt{2}$ cm？

(2)、经过多少时间后，△PCQ的面积为15 cm²？

(3)、设运动时间为t，用含t的代数式表示△PCQ的面积，并用配方法说明t为何值时△PCQ的面积最大，最大面积是多少？

查看试题解析

向上攀登的高度x/km	0.5	1.0	1.5	2.0
气温y/℃	2.0	﹣1.0	﹣4.0	﹣7.0