备考浙教版中考数学专项训练 数学思想
试卷更新日期:2022-05-18 类型:三轮冲刺
一、单选题
-
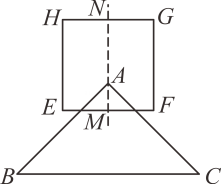
1. 如图,在边长为2的正方形 中, , 分别为 与 的中点,一个三角形 沿竖直方向向上平移,在运动的过程中,点 恒在直线 上,当点 运动到线段 的中点时,点 , 恰与 , 两边的中点重合.设点 到 的距离为 ,三角形 与正方形 的公共部分的面积为 ,则当 时, 的值为( )
 A、 或 B、 或 C、 D、 或2. 在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线 ( )与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是( )A、 B、 C、 D、 且3. 如图,把某矩形纸片 沿 , 折叠(点E、H在 边上,点F,G在 边上),使点B和点C落在 边上同一点P处,A点的对称点为 、D点的对称点为 ,若 , 为8, 的面积为2,则矩形 的长为( )
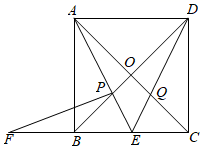
A、 或 B、 或 C、 D、 或2. 在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线 ( )与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是( )A、 B、 C、 D、 且3. 如图,把某矩形纸片 沿 , 折叠(点E、H在 边上,点F,G在 边上),使点B和点C落在 边上同一点P处,A点的对称点为 、D点的对称点为 ,若 , 为8, 的面积为2,则矩形 的长为( )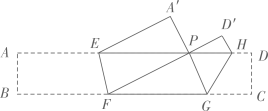 A、 B、 C、 D、4. 关于二次函数 的三个结论:①对任意实数m,都有 与 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则 或 ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则 或 .其中正确的结论是( )A、①② B、①③ C、②③ D、①②③5. 如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE , 分别交BD、AC于点P、Q , 过点P作PF⊥AE交CB的延长线于F , 下列结论:
A、 B、 C、 D、4. 关于二次函数 的三个结论:①对任意实数m,都有 与 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则 或 ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则 或 .其中正确的结论是( )A、①② B、①③ C、②③ D、①②③5. 如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE , 分别交BD、AC于点P、Q , 过点P作PF⊥AE交CB的延长线于F , 下列结论:①∠AED+∠EAC+∠EDB=90°,②AP=FP , ③AE= AO , ④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,⑤CE•EF=EQ•DE .
其中正确的结论有( )
 A、5个 B、4个 C、3个 D、2个6. 设三个互不相等的有理数,既可以表示为 的形式,也可以表示为 的形式,则 的值等于( )A、0 B、1 C、2 D、37. 如图,在 ▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中符合题意结论的个数共有( ).
A、5个 B、4个 C、3个 D、2个6. 设三个互不相等的有理数,既可以表示为 的形式,也可以表示为 的形式,则 的值等于( )A、0 B、1 C、2 D、37. 如图,在 ▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中符合题意结论的个数共有( ). A、1个 B、2个 C、3个 D、4个8. 若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )A、 B、2020 C、2019 D、20189. 平面内,到三角形三边所在直线距离相等的点共有( )个.A、3 B、4 C、5 D、610. 若一个直角三角形两边的长分别为6和8,则第三边的长为( )A、10 B、 C、10或 D、10或
A、1个 B、2个 C、3个 D、4个8. 若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )A、 B、2020 C、2019 D、20189. 平面内,到三角形三边所在直线距离相等的点共有( )个.A、3 B、4 C、5 D、610. 若一个直角三角形两边的长分别为6和8,则第三边的长为( )A、10 B、 C、10或 D、10或二、填空题
-
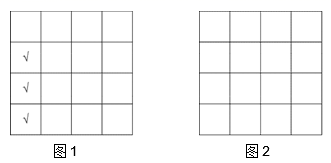
11. 为了预防新型冠状病毒的传染,人员之间需要保持一米以上的安全距离.某公司会议室共有四行四列座椅,并且相邻两个座椅之间的距离超过一米,为了保证更加安全,公司规定在此会议室开会时,每一行、每一列均不能有连续三人就座.例如图1中第一列所示情况不满足条件(其中“√”表示就座人员).根据该公司要求,该会议室最多可容纳的就座人数为人,并在图2中画出一种相应的座位安排示意图.
 12. 已知抛物线 (m为常数).(1)、若该抛物线经过点(1,m+7),求m的值;(2)、若抛物线上始终存在不重合的两点关于原点对称,求满足条件的最大整数m;(3)、将该抛物线向下平移若干个单位长度,所得的新抛物线经过P( , ),Q(7, )(其中 )两点,当 时,点P是该部分函数图象的最低点,求m的取值范围.13. 在平面直角坐标系xOy中,A(4,0),B(0,3),C(m , 7),三角形ABC的面积为14,则m的值为 .14. 如图,点E在 AC 的延长线上, ∠BAC 与 ∠DCE 的平分线交于点 F,∠B=58°, ∠F=56°,则∠BDC= .
12. 已知抛物线 (m为常数).(1)、若该抛物线经过点(1,m+7),求m的值;(2)、若抛物线上始终存在不重合的两点关于原点对称,求满足条件的最大整数m;(3)、将该抛物线向下平移若干个单位长度,所得的新抛物线经过P( , ),Q(7, )(其中 )两点,当 时,点P是该部分函数图象的最低点,求m的取值范围.13. 在平面直角坐标系xOy中,A(4,0),B(0,3),C(m , 7),三角形ABC的面积为14,则m的值为 .14. 如图,点E在 AC 的延长线上, ∠BAC 与 ∠DCE 的平分线交于点 F,∠B=58°, ∠F=56°,则∠BDC= .
 15. 如图,大正方形 中, ,小正方形 中, ,在小正方形绕 点旋转的过程中,当 时,线段 的长为 .
15. 如图,大正方形 中, ,小正方形 中, ,在小正方形绕 点旋转的过程中,当 时,线段 的长为 .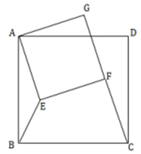 16. 如图,正方形ABCD和正方形AEFG中,点E在AD上,如果AB=3,那么△BDF的面积等于 .
16. 如图,正方形ABCD和正方形AEFG中,点E在AD上,如果AB=3,那么△BDF的面积等于 . 17. 如图,△ABC为等边三角形,点D、E分别在AC、AB上,且AD=BE , 连接BD、CE交于点P , 在△ABC外部作∠ABF=∠ABD , 过点A作AF⊥BF于点F , 若∠ADB=∠ABF+90°,BF﹣AF=3,则BP= .
17. 如图,△ABC为等边三角形,点D、E分别在AC、AB上,且AD=BE , 连接BD、CE交于点P , 在△ABC外部作∠ABF=∠ABD , 过点A作AF⊥BF于点F , 若∠ADB=∠ABF+90°,BF﹣AF=3,则BP= . 18. 如图,已知正方形ABCD的边长是1,点E是CD边上的中点.P为正方形ABCD边上的一个动点,动点P从A点出发,沿 运动,到达点E.若点P经过的路程为自变量x , 的面积为因变量y , 则当 时,x的值等于 .
18. 如图,已知正方形ABCD的边长是1,点E是CD边上的中点.P为正方形ABCD边上的一个动点,动点P从A点出发,沿 运动,到达点E.若点P经过的路程为自变量x , 的面积为因变量y , 则当 时,x的值等于 . 19. 如图,△ABC绕点A顺时针旋转45°得到△ ,若∠BAC=90°,AB=AC= ,则图中阴影部分的面积等于 .
19. 如图,△ABC绕点A顺时针旋转45°得到△ ,若∠BAC=90°,AB=AC= ,则图中阴影部分的面积等于 . 20. 如图,AD是△ABC的中线,E是AD上的一点,且AE= AD,CE交AB于点F。若AF=1.2cm,则AB=
20. 如图,AD是△ABC的中线,E是AD上的一点,且AE= AD,CE交AB于点F。若AF=1.2cm,则AB=
三、综合题
-
21. 请阅读下列解题过程:
解一元二次不等式:x2-5x>0.
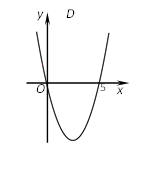
解:设x2-5x=0,解得:x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示).由图象可知:当x<0或x>5时函数图象位于x轴上方,此时y>0,即x2-5x>0.
所以一元二次不等式x2-5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)、上述解题过程中,渗透了下列数学思想中的和 . (只填序号)①转化思想;②分类讨论思想;③数形结合思想.
(2)、用类似的方法解一元二次不等式:x2-2x-3<0.22. 阅读材料:各类方程的解法求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想 转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)、问题:方程x3+x2-2x=0的解是x1=0,x2= , x3=;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长. 23. 阅读下列材料,完成相应任务.
23. 阅读下列材料,完成相应任务.下表是2019-2020赛季职业联赛积分榜(部分球队)
球队
比赛场数
胜场
负场
积分
广东东莞银行
30
28
2
58
新疆伊力特
29
22
7
51
辽宁本钢
30
20
10
50
山东西王
30
19
11
49
山西汾酒
30
18
12
48
福建豹发力
30
13
17
43
小明和小亮不仅热爱篮球,而且对联赛积分问题产生了浓厚的兴趣.他们提出的问题是:“胜一场、负一场分别积几分?”
(1)、小明的思路是:设胜一场积x分,则根据“广东东莞银行”胜负场数与积分的关系可以用含x的式子表示负一场的积分为 , 再根据“新疆伊力特”胜负场与积分的关系可列一元一次方程 .小亮的解法是:设胜一场积x分,负一场积y分,………………………第一步
可得二元一次方程组………………………第二步
由①,得③………………………第三步
将③代入②,得………………………第四步
解这个方程,得………………………第五步
将代入③中,得………………………第六步
解得………………………第七步
答:胜一场积2分,负一积1分.……………………第八步
任务1:将小明的思路中的空格处填起来;
(2)、任务2:小亮的解法中,列方程①②根据的等量关系分别是:方程①;方程②:;(3)、小亮解二元一次方程组的方法叫;(4)、小亮的解法中,第四步主要体现的数学思想是(选正确选项的代码)A.转化思想 B.一般到特殊思想
C.分类思想 D.数形结合思想
任务3:设胜一场积x分,负一场积y分,请你选择与小明和小亮不同的等量关系,列二元一次方程组 . (只列不解)
24. 如图,一次函数y=-x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点 .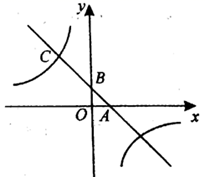 (1)、求反比例函数的解析式;(2)、若点P在y轴正半轴上,且与点B,C构成以 为腰的等腰三角形,请求出所有符合条件的P点坐标.25. 数学中,运用整体思想方法在求代数式的值时非常重要.
(1)、求反比例函数的解析式;(2)、若点P在y轴正半轴上,且与点B,C构成以 为腰的等腰三角形,请求出所有符合条件的P点坐标.25. 数学中,运用整体思想方法在求代数式的值时非常重要.例如:已知a2+2a=2,则代数式2a2+4a+3=2(a2+2a)+3=2×2+3=7.
请你根据以上材料解答以下问题:
(1)、若x2﹣3x=4,求1﹣x2+3x的值.(2)、当x=1时,代数式px3+qx﹣1的值是5,求当x=﹣1时,代数式px3+qx﹣1的值.(3)、当x=2020时,代数式ax5+bx3+cx+6的值为m , 直接写出当x=﹣2020时,代数式ax5+bx3+cx+6的值.(用含m的代数式表示)26. 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.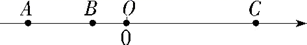 (1)、写出数轴上点A、C表示的数;(2)、点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN= CQ.设运动的时间为t(t>0)秒.
(1)、写出数轴上点A、C表示的数;(2)、点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN= CQ.设运动的时间为t(t>0)秒.①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?
27. 如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.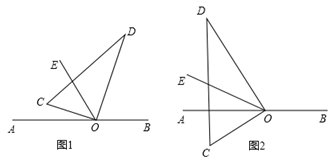 (1)、如图1,若∠COE=20°,则∠BOD=;若∠COE=α,则∠BOD=(用含α的代数式表示);(2)、将图1中三角板绕O逆时针旋转到图2的位置时,试猜测∠COE与∠BOD之间有怎样的数量关系,并说明理由.28. 已知,如图,实数a、b、c在数轴上表示的点分别是点A、B、C,且a、b、c满足 .
(1)、如图1,若∠COE=20°,则∠BOD=;若∠COE=α,则∠BOD=(用含α的代数式表示);(2)、将图1中三角板绕O逆时针旋转到图2的位置时,试猜测∠COE与∠BOD之间有怎样的数量关系,并说明理由.28. 已知,如图,实数a、b、c在数轴上表示的点分别是点A、B、C,且a、b、c满足 .
 (1)、求a、b、c的值;(2)、若点A沿数轴向左以每秒1个单位的速度运动,点B和点C沿数轴向右运动,速度分别是2个单位/秒、3个单位/秒.设运动时间为t(秒).
(1)、求a、b、c的值;(2)、若点A沿数轴向左以每秒1个单位的速度运动,点B和点C沿数轴向右运动,速度分别是2个单位/秒、3个单位/秒.设运动时间为t(秒).①求2秒后,点A、B、C表示的数;
②运动t秒后,求点B和点C之间的距离(用“BC”表示)和点A和点B之间的距离(用“AB”表示);(用含t的代数式表示)
③在②的基础上,请问:3×BC-AB的值是否随着时间t的变化而变化?若不变化,求这个不变的值;若变化,求这个值的变化范围;
(3)、若点A沿数轴向右以每秒1个单位的速度运动,点B和点C沿数轴向左运动,速度分别是2个单位/秒、3个单位/秒.设运动时间为t(秒).是否存在某一时刻,满足点A和点B之间的距离是点B和点C之间的距离的 ?若存在,直接写出时间t的值;若不存在,说明理由.29. 如图,抛物线y=ax2+bx+3经过A (1,0)、B(4,0)两点,与y轴交于点C. (1)、求该抛物线的解析式;(2)、如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;不存在,请说明理由.(3)、在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.30. 如图,直线 与双曲线 的图象相交于点A和点C,点A的坐标为(-1, a),点C的坐标为(b,-1).
(1)、求该抛物线的解析式;(2)、如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;不存在,请说明理由.(3)、在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.30. 如图,直线 与双曲线 的图象相交于点A和点C,点A的坐标为(-1, a),点C的坐标为(b,-1). (1)、求a的值和反比例函数的解析式;(2)、求b的值,并直接写出使得反比例函数大于一次函数的值的x的取值范围;(3)、如图,直线 与x轴相交于点B,在x轴上存在点D,使得△BCD是以BC为腰的等腰三角形,求点D的坐标.
(1)、求a的值和反比例函数的解析式;(2)、求b的值,并直接写出使得反比例函数大于一次函数的值的x的取值范围;(3)、如图,直线 与x轴相交于点B,在x轴上存在点D,使得△BCD是以BC为腰的等腰三角形,求点D的坐标.