备考浙教版中考数学题型专项训练 图形的变换解答题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、综合题
-
1. 已知△ABC中,AB=AC,∠BAC=α(α<90°),CD⊥AB于点D,点E是AC边上一动点(不与点C重合),EF⊥BC于点F,EF与CD交于点G.

 (1)、当E点与A点重合时,如图1,若α=45°,猜想CF与EG的数量关系.(2)、当E点与A点不重合时,
(1)、当E点与A点重合时,如图1,若α=45°,猜想CF与EG的数量关系.(2)、当E点与A点不重合时,①若α=45°,如图2,第(1)题中的结论是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
②若α≠45°,如图3,请直接写出的值(用含有α的三角函数表示).
2. 已知直角三角形ABC中, , , , 动点P从点A出发,以每秒3个单位的速度沿折线向终点C运动,且不与的顶点重合,点D为边AB的中点,当点P不与点D重合时,过点P作线段PD的垂线与的一边交于点Q,构造 , 设点P的运动时间为t(). (1)、线段BC的长为 .(2)、点P在线段AB上运动时,用t表示线段PD的长.(3)、点P在线段AB上运动,当是以DQ为腰的等腰三角形时,求t的值.(4)、当点P经过点D后,作点Q关于PD的对称点为 , 当时,直接写出t的值.3. 如图,△ABC与△DEF都是等腰直角三角形,AC=BC,DE=DF.边AB,EF的中点重合于点O,连接BF,CD.
(1)、线段BC的长为 .(2)、点P在线段AB上运动时,用t表示线段PD的长.(3)、点P在线段AB上运动,当是以DQ为腰的等腰三角形时,求t的值.(4)、当点P经过点D后,作点Q关于PD的对称点为 , 当时,直接写出t的值.3. 如图,△ABC与△DEF都是等腰直角三角形,AC=BC,DE=DF.边AB,EF的中点重合于点O,连接BF,CD. (1)、如图①,当FE⊥AB时,易证BF=CD(不需证明);
(1)、如图①,当FE⊥AB时,易证BF=CD(不需证明);当△DEF绕点O旋转到如图②位置时,猜想BF与CD之间的数量关系,并证明;
(2)、当△ABC与△DEF均为等边三角形时,其他条件不变,如图③,猜想BF与CD之间的数量关系,直接写出你的猜想,不需证明.4. 数学兴趣小组在学习平行四边形的性质后,开始进一步的探索.他们将平行四边形沿着它的一条对角线翻折,发现其中还有很多结论:如图①,在平行四边形ABCD中, , 将沿AC翻折至 , 连接 .
 (1)、【发现与证明】发现△AB′C与平行四边形ABCD重叠部分的图形始终是____;A、等腰三角形; B、等边三角形; C、直角三角形(2)、【应用与探究】求证: .
(1)、【发现与证明】发现△AB′C与平行四边形ABCD重叠部分的图形始终是____;A、等腰三角形; B、等边三角形; C、直角三角形(2)、【应用与探究】求证: .如图②,在平行四边形ABCD中,已知 , 将沿AC翻折至 , 连接 . 若 , , 则°, .
5. 如图1,在▱ABCD中,AB= , AD=2,△A'BD与△ABD关于BD对称,A'B交边CD于点E. (1)、求证:△A'DE≌△CBE.(2)、延长A'C到点F,使得A'C=CF,连结BF.
(1)、求证:△A'DE≌△CBE.(2)、延长A'C到点F,使得A'C=CF,连结BF.①若BF⊥A'F,求A'C的长.
②如图2,若∠F=∠A'BD,记四边形ABED的面积为S1 , △BCE的面积为S2 , 求S1-S2的值.(直接写出答案即可)
6. 矩形中,、交于点O,(k为常数).作 , 、分别与、边相交于点E、F,连接 , (1)、发现问题:如图1,若 , 猜想:;(2)、类比探究:如图2, , 探究线段 , 之间的数量关系,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,若 , , , 求的长.7. 已知:正方形中, , 将绕点A顺时针旋转,它的两边分别交、(或它们的延长线)于点M、N.
(1)、发现问题:如图1,若 , 猜想:;(2)、类比探究:如图2, , 探究线段 , 之间的数量关系,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,若 , , , 求的长.7. 已知:正方形中, , 将绕点A顺时针旋转,它的两边分别交、(或它们的延长线)于点M、N.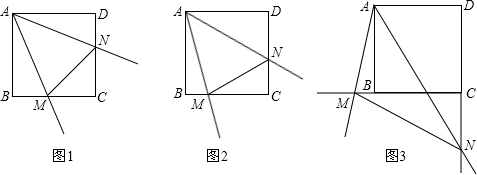 (1)、如图1,当绕点A旋转到时,有 . 当绕点A旋转到时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)、当绕点A旋转到如图3的位置时,线段和之间有怎样的等量关系?请写出你的猜想,并证明.8. 阅读资料:如图1,在平面之间坐标系中, , 两点的坐标分别为 , , 由勾股定理得 , 所以 , 两点间的距离为 . 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系中,为圆上任意一点,则到原点的距离的平方为 , 当的半径为时,的方程可写为: .
(1)、如图1,当绕点A旋转到时,有 . 当绕点A旋转到时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)、当绕点A旋转到如图3的位置时,线段和之间有怎样的等量关系?请写出你的猜想,并证明.8. 阅读资料:如图1,在平面之间坐标系中, , 两点的坐标分别为 , , 由勾股定理得 , 所以 , 两点间的距离为 . 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系中,为圆上任意一点,则到原点的距离的平方为 , 当的半径为时,的方程可写为: .问题拓展:如果圆心坐标为 , 半径为 , 那么的方程可以写为 .
综合应用:如图3,与轴相切于原点 , 点坐标为 , 是上一点,连接 , 使 , 作 , 垂足为 , 延长交轴于点 , 连接 .
 (1)、求证是的切线;(2)、是否存在到四点 , , , 距离都相等的点?若存在,求点坐标,并写出以为圆心,以为半径的的方程;若不存在,说明理由.9. 如图1,抛物线y=﹣x2+bx+c经过点A(﹣1,0)、B(3,0).
(1)、求证是的切线;(2)、是否存在到四点 , , , 距离都相等的点?若存在,求点坐标,并写出以为圆心,以为半径的的方程;若不存在,说明理由.9. 如图1,抛物线y=﹣x2+bx+c经过点A(﹣1,0)、B(3,0). (1)、求抛物线的函数表达式:(2)、设抛物线的顶点为D,与y轴相交与点C,连接AC、CD、BC、BD,请你判断∠ACO与∠DBC的数量关系,并说明理由;(3)、如图2,连接AD,与BC相交于点E,点G是抛物线上一动点,在对称轴上是否存在点F,使得∠EFG=90°,且tan∠FEG=如果存在,请求出点F的坐标;如果不存在,请说明理由.10. 在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(不与点B、点C重合),将线段AD绕A逆时针旋转90°得到线段AE,作射线BA与射线CE,两射线交于点F.
(1)、求抛物线的函数表达式:(2)、设抛物线的顶点为D,与y轴相交与点C,连接AC、CD、BC、BD,请你判断∠ACO与∠DBC的数量关系,并说明理由;(3)、如图2,连接AD,与BC相交于点E,点G是抛物线上一动点,在对称轴上是否存在点F,使得∠EFG=90°,且tan∠FEG=如果存在,请求出点F的坐标;如果不存在,请说明理由.10. 在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(不与点B、点C重合),将线段AD绕A逆时针旋转90°得到线段AE,作射线BA与射线CE,两射线交于点F. (1)、若点D在线段BC上,如图1,请直接写出CD与EF的关系.(2)、若点D在线段BC的延长线上,如图2,(1)中的结论还成立吗?请说明理由.(3)、在(2)的条件下,连接DE,G为DE的中点,连接GF,若tan∠AEC= , AB= , 求GF的长.11. 如图,AD是△ABC的角平分线, , 以AC上一点O为圆心,作过点A和点D的⊙O,与AC交于另一点E,连接DE
(1)、若点D在线段BC上,如图1,请直接写出CD与EF的关系.(2)、若点D在线段BC的延长线上,如图2,(1)中的结论还成立吗?请说明理由.(3)、在(2)的条件下,连接DE,G为DE的中点,连接GF,若tan∠AEC= , AB= , 求GF的长.11. 如图,AD是△ABC的角平分线, , 以AC上一点O为圆心,作过点A和点D的⊙O,与AC交于另一点E,连接DE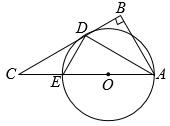 (1)、求证:BC是⊙O的切线;(2)、若 , , 求⊙O的半径12. 如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF,AF.
(1)、求证:BC是⊙O的切线;(2)、若 , , 求⊙O的半径12. 如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF,AF.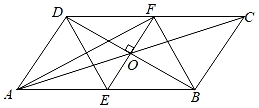 (1)、求证:四边形DEBF是菱形;(2)、设ADEF,AD+AB=12,BD=4 , 求AF的长.13. 如图1,在中, , AB是的直径,交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是的切线.
(1)、求证:四边形DEBF是菱形;(2)、设ADEF,AD+AB=12,BD=4 , 求AF的长.13. 如图1,在中, , AB是的直径,交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是的切线.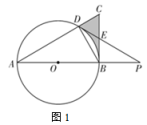 (1)、求证:;(2)、若 , , 求图中阴影部分的周长和面积;(3)、如图2, , 连接DM,交AB于点N,若 , 求的值.
(1)、求证:;(2)、若 , , 求图中阴影部分的周长和面积;(3)、如图2, , 连接DM,交AB于点N,若 , 求的值.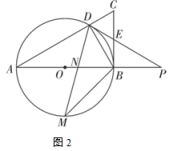 14. 如图,△ABC内接于⊙O(∠ACB>90°),连接OA,OC.记∠BAC=α,∠BCO=β,∠BAO=γ.
14. 如图,△ABC内接于⊙O(∠ACB>90°),连接OA,OC.记∠BAC=α,∠BCO=β,∠BAO=γ.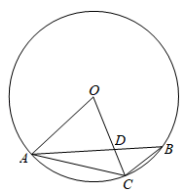 (1)、探究α与β之间的数量关系,并证明.(2)、设OC与AB交于点D,⊙O半径为1,
(1)、探究α与β之间的数量关系,并证明.(2)、设OC与AB交于点D,⊙O半径为1,①若β=γ+45°,AD=2OD,求由线段BD,CD,弧BC围成的图形面积S.
②若α+2γ=90°,设sinα=k,用含k的代数式表示线段OD的长.
15. 如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.
请你帮助小刚的学习小组解决下面的问题:
(1)、盲区1的面积约是m2;盲区2的面积约是m2;(≈1.4,≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,结果保留整数)(2)、如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域.16. 如图,⊙O的弦AC与BD互相垂直于点E,OA交ED于点F. (1)、如图(1),求证:∠BAC=∠OAD;(2)、如图(2),当AC=CD时,求证:AB=BF;(3)、如图(3),在(2)的条件下,点P,Q在CD上,点P为CQ中点,∠POQ=∠OFD,DF=EC,DQ=6,求AB的长.17. 在中, , 以点D为圆心,适当的长度为半径画弧,分别交边AD、CD于点M、N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点K,作射线DK,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转得线段EP.
(1)、如图(1),求证:∠BAC=∠OAD;(2)、如图(2),当AC=CD时,求证:AB=BF;(3)、如图(3),在(2)的条件下,点P,Q在CD上,点P为CQ中点,∠POQ=∠OFD,DF=EC,DQ=6,求AB的长.17. 在中, , 以点D为圆心,适当的长度为半径画弧,分别交边AD、CD于点M、N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点K,作射线DK,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转得线段EP.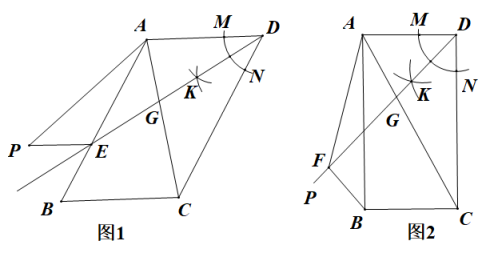 (1)、如图1,当时,连接AP,线段AP和线段AC的数量关系为;(2)、如图2,当时,过点B作于点F,连接AF,请求出∠FAC的度数,以及AF,AB,AD之间的数量关系,并说明理由;(3)、当时,连接AP,若 , 请直接写出线段AP与线段DG的比值.18. 定义:四边形ABCD中,AB=AC,∠BDC=∠BAC,则称四边形ABCD为半角四边形,边BC称为半对边.
(1)、如图1,当时,连接AP,线段AP和线段AC的数量关系为;(2)、如图2,当时,过点B作于点F,连接AF,请求出∠FAC的度数,以及AF,AB,AD之间的数量关系,并说明理由;(3)、当时,连接AP,若 , 请直接写出线段AP与线段DG的比值.18. 定义:四边形ABCD中,AB=AC,∠BDC=∠BAC,则称四边形ABCD为半角四边形,边BC称为半对边. (1)、如图①,若四边形ABCD为半角四边形,且BC为半对边,设∠DBC=α,用含有α的代数式表示∠ACD;(2)、如图②,等腰△ABC,AB=AC,点D为其内部一点,∠ABD=∠ACD,连结AD,作△ACD的外接圆⊙O,BD的延长线交⊙O于点E,连结EA,EC,求证:四边形ABCE为半角四边形;(3)、如图③,在(2)的条件下,延长BA交⊙O于点F,连结EF,EF∥BC.
(1)、如图①,若四边形ABCD为半角四边形,且BC为半对边,设∠DBC=α,用含有α的代数式表示∠ACD;(2)、如图②,等腰△ABC,AB=AC,点D为其内部一点,∠ABD=∠ACD,连结AD,作△ACD的外接圆⊙O,BD的延长线交⊙O于点E,连结EA,EC,求证:四边形ABCE为半角四边形;(3)、如图③,在(2)的条件下,延长BA交⊙O于点F,连结EF,EF∥BC.①求证:BC=CE;
②若AD=3,BC=6 , 求四边形ADEF的面积.
19. 如图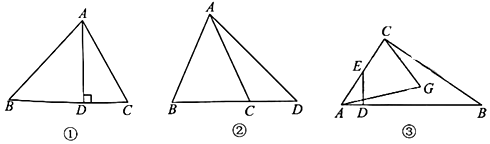 (1)、【基础巩固】如图①,在△ABC中,AD⊥BC于点D,若BD=3,CD=1,求AB2-AC2的值;(2)、【尝试应用】如图②,点C在△ABD的边BD上,满足AB=AC,求证:AD2-AC2=BD·CD;(3)、【拓展提高】如图③,已知点D为Rt△ABC斜边上一点,过点D作AB的垂线,交AC于点E,点G在CE的中垂线上,连结AG,若CG=BD,求证:求证:AG=(AD+AB).20. 如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)、【基础巩固】如图①,在△ABC中,AD⊥BC于点D,若BD=3,CD=1,求AB2-AC2的值;(2)、【尝试应用】如图②,点C在△ABD的边BD上,满足AB=AC,求证:AD2-AC2=BD·CD;(3)、【拓展提高】如图③,已知点D为Rt△ABC斜边上一点,过点D作AB的垂线,交AC于点E,点G在CE的中垂线上,连结AG,若CG=BD,求证:求证:AG=(AD+AB).20. 如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.

 (1)、操作发现如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在BC边上时,填空:
(1)、操作发现如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在BC边上时,填空:
①线段DE与AC的位置关系是;②设△BDC的面积为S1 , △AEC的面积为S2 . 则S1与S2的数量关系是 .
(2)、猜想论证当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
21. 如图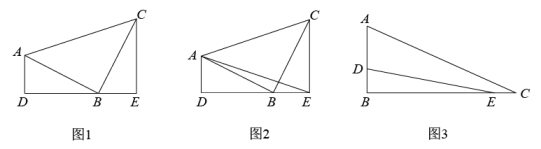 (1)、如图1,为等腰直角三角形, , 求证:.(2)、如图2,在(1)的条件下,连结 , , 求的长.(3)、如图3,在中, , 分别在直角边 , 上, , , 求.22. 如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.
(1)、如图1,为等腰直角三角形, , 求证:.(2)、如图2,在(1)的条件下,连结 , , 求的长.(3)、如图3,在中, , 分别在直角边 , 上, , , 求.22. 如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.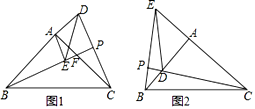 (1)、如图1,连接BE,CD,BE的延长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)、如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6 , AD=3,求△PDE的面积.23. 如图,在矩形ABCD中,AB=2,BC=4,点E在直线AB上,连结DE,过点A作AF⊥DE交直线BC于点F,以AE、AF为邻边作平行四边形AEGF.直线DG交直线AB于点H.
(1)、如图1,连接BE,CD,BE的延长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)、如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6 , AD=3,求△PDE的面积.23. 如图,在矩形ABCD中,AB=2,BC=4,点E在直线AB上,连结DE,过点A作AF⊥DE交直线BC于点F,以AE、AF为邻边作平行四边形AEGF.直线DG交直线AB于点H. (1)、当点E在线段AB上时,求证:△ABF ∽△DAE.(2)、当AE=2时,求EH的长.(3)、在点E的运动过程中,是否存在某一位置,使得△EGH为等腰三角形.若存在,求AE的长.24. 教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
(1)、当点E在线段AB上时,求证:△ABF ∽△DAE.(2)、当AE=2时,求EH的长.(3)、在点E的运动过程中,是否存在某一位置,使得△EGH为等腰三角形.若存在,求AE的长.24. 教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
请根据教材提示,结合图①,写出完整的证明过程.

结论应用:在 ▱ ABCD中,对角线AC、BD、交于点O,E为边BC的中点,AE、BD交于点F.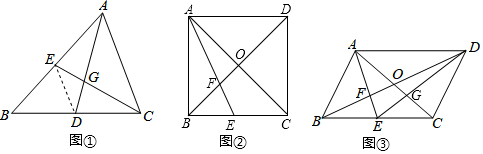 (1)、如图②,若为正方形,且 , 则的长为_.(2)、如图③,连结交于点 , 若四边形的面积为 , 则的面积为_.25. 如图,是的外接圆,点在上,连结 , , , 过点作的平行线交于点.
(1)、如图②,若为正方形,且 , 则的长为_.(2)、如图③,连结交于点 , 若四边形的面积为 , 则的面积为_.25. 如图,是的外接圆,点在上,连结 , , , 过点作的平行线交于点.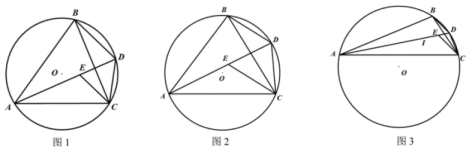 (1)、如图1,求证:;(2)、如图2,若 , , , 求;(3)、如图3,为的内心,若在线段上, , , 当最大时,求出的半径.26. 如图
(1)、如图1,求证:;(2)、如图2,若 , , , 求;(3)、如图3,为的内心,若在线段上, , , 当最大时,求出的半径.26. 如图 (1)、如图①,在△ABC中,AB=AC=2,∠A=120°,则S△ABC=;(2)、如图②,在△ABC中,AB的垂直平分线交BC于D,交AB于点M,AC的垂直平分线交BC于E,交AC于N,∠DAE=20°,BC=6,求∠BAC的度数及△ADE的周长;(3)、如图③,某农场主欲规划出一个如图所示的矩形田地ABCD,其中BC=0.4km,点P在边AD上,E、F为BC边上两点(包括端点),在△PEF区域种植甲种农作物,其余区域种植乙种农作物,并沿△PEF的三边铺设围栏,围栏总长为0.6km(即△PEF的周长为0.6km),围栏PE与PF的夹角为60°(即∠EPF=60°),为了尽可能多的种植农作物要求矩形ABCD的面积尽可能的大,请问能否设计出一个面积尽可能大又满足要求的矩形ABCD田地?若能,求出矩形ABCD面积的最大值;若不能,请说明理由.27. 如图
(1)、如图①,在△ABC中,AB=AC=2,∠A=120°,则S△ABC=;(2)、如图②,在△ABC中,AB的垂直平分线交BC于D,交AB于点M,AC的垂直平分线交BC于E,交AC于N,∠DAE=20°,BC=6,求∠BAC的度数及△ADE的周长;(3)、如图③,某农场主欲规划出一个如图所示的矩形田地ABCD,其中BC=0.4km,点P在边AD上,E、F为BC边上两点(包括端点),在△PEF区域种植甲种农作物,其余区域种植乙种农作物,并沿△PEF的三边铺设围栏,围栏总长为0.6km(即△PEF的周长为0.6km),围栏PE与PF的夹角为60°(即∠EPF=60°),为了尽可能多的种植农作物要求矩形ABCD的面积尽可能的大,请问能否设计出一个面积尽可能大又满足要求的矩形ABCD田地?若能,求出矩形ABCD面积的最大值;若不能,请说明理由.27. 如图 (1)、问题提出:如图1,在△ABC中,D为BC上一点,且满足 , 则△ABC形状为 . (请填写序号:①钝角三角形;②直角三角形;③锐角三角形)(2)、问题探究:如图2,四边形ABCD为的内接四边形, , , 连接AC、BD,若 , 则对角线AC的长度为多少?(3)、问题解决:如图3,在四边形ABCD中, , , , 以C为圆心,CB长为半径画 , M为上的一动点,过点M作 , , 连接EF.已知 , 探究:线段EF是否存在最小长度?若存在,请求出EF的最小长度;若不存在,请说明理由.28. 将一副三角板中的两块直角三角尺的直角顶点C按照如图①的方式叠放在一起(∠A = 30°,∠ABC = 60°,∠E = ∠EDC = 45°),且三角板ACB的位置保持不动.
(1)、问题提出:如图1,在△ABC中,D为BC上一点,且满足 , 则△ABC形状为 . (请填写序号:①钝角三角形;②直角三角形;③锐角三角形)(2)、问题探究:如图2,四边形ABCD为的内接四边形, , , 连接AC、BD,若 , 则对角线AC的长度为多少?(3)、问题解决:如图3,在四边形ABCD中, , , , 以C为圆心,CB长为半径画 , M为上的一动点,过点M作 , , 连接EF.已知 , 探究:线段EF是否存在最小长度?若存在,请求出EF的最小长度;若不存在,请说明理由.28. 将一副三角板中的两块直角三角尺的直角顶点C按照如图①的方式叠放在一起(∠A = 30°,∠ABC = 60°,∠E = ∠EDC = 45°),且三角板ACB的位置保持不动. (1)、将三角板DCE绕点C按顺时针方向旋转至图②,若∠ACE = 60°,求∠DCB的度数.(2)、将三角板DCE绕点C按顺时针方向旋转,当旋转到ED∥AB时,求∠BCE的度数(请先在备用图上补全相应的图形).(3)、当0° < ∠BCE < 180°且点E在直线BC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠BCE所有可能的值;若不存在,请说明理由.29. 我们把三角形三边上的高产生的三个垂足组成的三角形称为该三角形的垂足三角形.
(1)、将三角板DCE绕点C按顺时针方向旋转至图②,若∠ACE = 60°,求∠DCB的度数.(2)、将三角板DCE绕点C按顺时针方向旋转,当旋转到ED∥AB时,求∠BCE的度数(请先在备用图上补全相应的图形).(3)、当0° < ∠BCE < 180°且点E在直线BC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠BCE所有可能的值;若不存在,请说明理由.29. 我们把三角形三边上的高产生的三个垂足组成的三角形称为该三角形的垂足三角形. (1)、如图1,△ABC中,AB=AC=8,BC=6,△DEF是△ABC的垂足三角形,求DE的长.(2)、如图2,圆内接三角形ABC中,AB=AC=x,BC=6,△ABC的垂足三角形DEF的周长为y.
(1)、如图1,△ABC中,AB=AC=8,BC=6,△DEF是△ABC的垂足三角形,求DE的长.(2)、如图2,圆内接三角形ABC中,AB=AC=x,BC=6,△ABC的垂足三角形DEF的周长为y.①求y与x的关系式;
②若△DEF的周长为 时,求⊙O的半径.
30. 如图,在矩形ABCD中,BC=1,AB=2,过对角线BD上一点P作AB的垂线交AB于点F,交CD于点E,过点E作EG∥BD交BC于点G,连接FG交BD于点H,连接DF.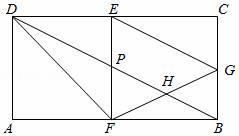 (1)、求 的值.(2)、当四边形DFGE有一组邻边相等时,求BG的长.(3)、点B关于FG的对称点记为B',若B'落在△EFG内部(不包含边界),求DP长度的取值范围.
(1)、求 的值.(2)、当四边形DFGE有一组邻边相等时,求BG的长.(3)、点B关于FG的对称点记为B',若B'落在△EFG内部(不包含边界),求DP长度的取值范围.