备考浙教版中考数学题型专项训练 图形的变换选择题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、单选题
-
1. 如图,在边长为4的正方形ABCD中,点E,F分别是边BC, AB的中点,连接AE,DF交于点O,将△ABE沿AE翻折,得到△AGE,延长EG交AD的延长线于点H,连接CG.有以下结论:①AE⊥DF;②AH=EH;③;④S四边形BEOF :S△AOF=4,其中正确的有( )
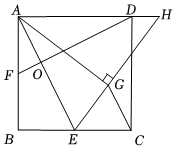 A、1个 B、2个 C、3个 D、4个2. 如图,E为正方形ABCD边AB上一动点(不与A重合),AB=4,将△DAE绕着点A逆时针旋转90°得到△BAF,再将△DAE沿直线DE折叠得到△DME.下列结论:①连结AM,则AM∥FB;②连结FE,当F、E、M共线时,AE=4-4;③连结EF、EC、FC,若△FEC是等腰三角形,则AE=4-4;④连结EF,设FC、ED交于点O,若FE平分∠BFC,则O是FC的中点,且AE=2-2,其中正确的个数有( )个.
A、1个 B、2个 C、3个 D、4个2. 如图,E为正方形ABCD边AB上一动点(不与A重合),AB=4,将△DAE绕着点A逆时针旋转90°得到△BAF,再将△DAE沿直线DE折叠得到△DME.下列结论:①连结AM,则AM∥FB;②连结FE,当F、E、M共线时,AE=4-4;③连结EF、EC、FC,若△FEC是等腰三角形,则AE=4-4;④连结EF,设FC、ED交于点O,若FE平分∠BFC,则O是FC的中点,且AE=2-2,其中正确的个数有( )个. A、4 B、3 C、2 D、13. 如图,菱形ABCD中,AE=1,AF=BE=2.若P为对角线BD 上一动点,则EP+FP的最小值为( )
A、4 B、3 C、2 D、13. 如图,菱形ABCD中,AE=1,AF=BE=2.若P为对角线BD 上一动点,则EP+FP的最小值为( )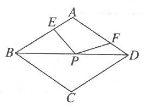 A、1 B、2 C、3 D、44. 如图,在Rt△ABC中, , ,把 折叠,使 落在 上,点 与 上的点 重合,展开后,折痕 交 于点 ,连接 、 , 交 于 点.下列结论:① ②若将 沿 折叠,则点 一定落在 上③图中有7个等腰三角形④若 ,则 ⑤ ,上述结论中正确的个数是( )
A、1 B、2 C、3 D、44. 如图,在Rt△ABC中, , ,把 折叠,使 落在 上,点 与 上的点 重合,展开后,折痕 交 于点 ,连接 、 , 交 于 点.下列结论:① ②若将 沿 折叠,则点 一定落在 上③图中有7个等腰三角形④若 ,则 ⑤ ,上述结论中正确的个数是( )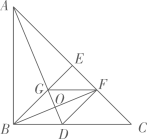 A、2个 B、3个 C、4个 D、5个5. 如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A、2个 B、3个 C、4个 D、5个5. 如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( ) A、①②④ B、②③④ C、②③ D、②④6. 如图,在和中, , , , 点M、N、P分别为EF、BC、CE的中点,若绕点A在平面内自由旋转,面积的最大值为( )
A、①②④ B、②③④ C、②③ D、②④6. 如图,在和中, , , , 点M、N、P分别为EF、BC、CE的中点,若绕点A在平面内自由旋转,面积的最大值为( ) A、24 B、18 C、12 D、207. 如图,在正方形ABCD中,F为CD上一点,AF交对角线BD于点E,点G是BC上的一点且AE=EG,连结AG,交BD于点H.满足AH2=HE•HD,现给出下列结论:①EG⊥AF;②BG+DF=FG;③若 ,则 .其中正确的有( )个.
A、24 B、18 C、12 D、207. 如图,在正方形ABCD中,F为CD上一点,AF交对角线BD于点E,点G是BC上的一点且AE=EG,连结AG,交BD于点H.满足AH2=HE•HD,现给出下列结论:①EG⊥AF;②BG+DF=FG;③若 ,则 .其中正确的有( )个. A、0 B、1 C、2 D、38. 在平面直角坐标系中,已知点A(3,﹣3),在坐标轴上确定一点B,使△AOB为等腰三角形,则符合条件的点B共有( )个A、5 B、6 C、7 D、89. 如图,已知直线l1∥l2 , l1、l2之间的距离AE为 ,在△ABC中,BC=2,AB= ,将△ABC绕点C在平面内顺时针旋转得到△A′B′C,若旋转角为60°,A′C交直线l2于点D,则CD的长度为( )
A、0 B、1 C、2 D、38. 在平面直角坐标系中,已知点A(3,﹣3),在坐标轴上确定一点B,使△AOB为等腰三角形,则符合条件的点B共有( )个A、5 B、6 C、7 D、89. 如图,已知直线l1∥l2 , l1、l2之间的距离AE为 ,在△ABC中,BC=2,AB= ,将△ABC绕点C在平面内顺时针旋转得到△A′B′C,若旋转角为60°,A′C交直线l2于点D,则CD的长度为( ) A、 B、 C、 D、 ﹣10. 如图, 中, , , ,点 是 边上的一个动点,将线段 绕点 顺时针旋转 得到线段 ,连接 ,则在点 运动过程中,线段 的最小值为( )
A、 B、 C、 D、 ﹣10. 如图, 中, , , ,点 是 边上的一个动点,将线段 绕点 顺时针旋转 得到线段 ,连接 ,则在点 运动过程中,线段 的最小值为( ) A、 B、 C、 D、11. 如图,正方形ABCD边长为2,BM、DN分别是正方形的两个外角的平分线,点P,Q分别是平分线BM、DN上的点,且满足∠PAQ=45°,连接PQ、PC、CQ.则下列结论:①BP•DQ=3.6;②∠QAD=∠APB;③∠PCQ=135°;④ . 其中正确的有( )
A、 B、 C、 D、11. 如图,正方形ABCD边长为2,BM、DN分别是正方形的两个外角的平分线,点P,Q分别是平分线BM、DN上的点,且满足∠PAQ=45°,连接PQ、PC、CQ.则下列结论:①BP•DQ=3.6;②∠QAD=∠APB;③∠PCQ=135°;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个12. 如图,锐角△ABC中,BC=6 ,S△ABC=12 ,两动点M 、 N分别在边 AB 、AC上滑动,且MN∥BC,以MN 为边向下作正方形MNPQ ,设其边长为x ,正方形MNPQ 与 △ABC公共部分的面积为y ,则y与x的函数图象大致是( )
A、1个 B、2个 C、3个 D、4个12. 如图,锐角△ABC中,BC=6 ,S△ABC=12 ,两动点M 、 N分别在边 AB 、AC上滑动,且MN∥BC,以MN 为边向下作正方形MNPQ ,设其边长为x ,正方形MNPQ 与 △ABC公共部分的面积为y ,则y与x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 13. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )
13. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )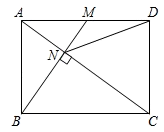 A、①②③④ B、①②③ C、①②④ D、②③④14. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( )
A、①②③④ B、①②③ C、①②④ D、②③④14. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( ) A、 B、 C、 D、15. 如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt△ABC中, , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连接KN交AG于点M,若 , 则为( )
A、 B、 C、 D、15. 如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt△ABC中, , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连接KN交AG于点M,若 , 则为( )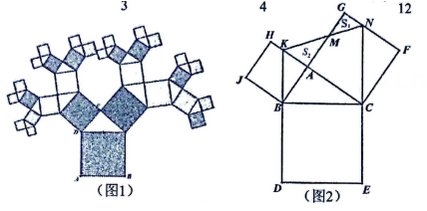 A、 B、 C、 D、16. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B—C—A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( )
A、 B、 C、 D、16. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B—C—A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( ) A、
A、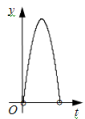 B、
B、 C、
C、 D、
D、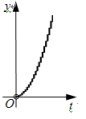 17. 如图,在中, , 以斜边AB为边向下做正方形ADEB,过点E作交AC于点F,过点C作交EF于点G,连结DG,若 , , 则四边形CGEB的面积为( )
17. 如图,在中, , 以斜边AB为边向下做正方形ADEB,过点E作交AC于点F,过点C作交EF于点G,连结DG,若 , , 则四边形CGEB的面积为( ) A、81 B、90 C、100 D、12018. 如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,AC与EF相交于点G,若 , ,则FG的长为( )
A、81 B、90 C、100 D、12018. 如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,AC与EF相交于点G,若 , ,则FG的长为( ) A、 B、2 C、3 D、419. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( )
A、 B、2 C、3 D、419. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( ) A、 B、 C、 D、220. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )
A、 B、 C、 D、220. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )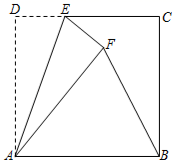 A、1 B、 C、 D、21. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A、1 B、 C、 D、21. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )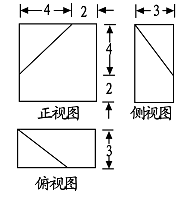 A、108cm3 B、100 cm3 C、92cm3 D、84cm322. 下列几何体中,主视图和左视图都为矩形的是( )A、
A、108cm3 B、100 cm3 C、92cm3 D、84cm322. 下列几何体中,主视图和左视图都为矩形的是( )A、 B、
B、 C、
C、 D、
D、 23.
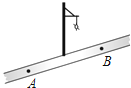
23.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来,大致图象是( )
 A、
A、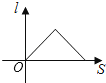
B、
B、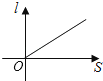
C、
C、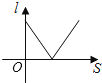
D、
D、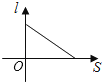 24.
24.如图是由5个完全相同的小正方体组成的几何体.则这个几何体的主视图是( )
 A、
A、
B、
B、
C、
C、 D、
D、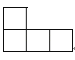
25.
25.一个几何体的三视图如图所示,则该几何体的形状可能是( )
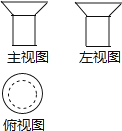 A、
A、 B、
B、 C、
C、 D、
D、 26. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( )
26. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( ) A、4 B、 C、 D、27. 如图,△ABC中,AB=AC= ,∠BAC=α°, ,G为BC中点,D为平面内一个动点,且 .将线段BD绕点D逆时针旋转α°,得到DB′,则四边形BACB′面积的最大值为( )
A、4 B、 C、 D、27. 如图,△ABC中,AB=AC= ,∠BAC=α°, ,G为BC中点,D为平面内一个动点,且 .将线段BD绕点D逆时针旋转α°,得到DB′,则四边形BACB′面积的最大值为( )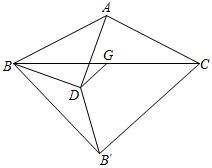 A、24 B、25 C、12 D、1328. 如图,边长为10的等边 中,点 在边 上,且 ,将含30°角的直角三角板( )绕直角顶点 旋转, 、 分别交边 、 于 、 .连接 ,当 时, 长为( )
A、24 B、25 C、12 D、1328. 如图,边长为10的等边 中,点 在边 上,且 ,将含30°角的直角三角板( )绕直角顶点 旋转, 、 分别交边 、 于 、 .连接 ,当 时, 长为( ) A、6 B、 C、10 D、
A、6 B、 C、10 D、

