备考浙教版中考数学题型专项训练 图形的性质解答题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、综合题
-
1. 如图,在 中, , , 平分 ,交 边于点 .
 (1)、如图1,过点A作AD⊥BC于D ,若已知∠C=50° ,求∠EAD 度数;(2)、如图2,过点 作 于 ,若 恰好又平分 ,求 的度数;(3)、如图3,CF平分△ABC 外角∠BCG ,交AE的延长线于点 F,作FD⊥BC 于D ,设∠ACB=n° ,试求∠DFE-∠AFC 的值.(用含有n的代数式表示)
(1)、如图1,过点A作AD⊥BC于D ,若已知∠C=50° ,求∠EAD 度数;(2)、如图2,过点 作 于 ,若 恰好又平分 ,求 的度数;(3)、如图3,CF平分△ABC 外角∠BCG ,交AE的延长线于点 F,作FD⊥BC 于D ,设∠ACB=n° ,试求∠DFE-∠AFC 的值.(用含有n的代数式表示)
(4)、如图4,在图3的基础上分别作 和 的角平分线,交于点 ,作 于 ,设 ,试直接写出 的值.(用含有 的代数式表示)2. 已知:直线AB∥CD,M,N分别在直线AB,CD上,H为平面内一点,连HM,HN. (1)、如图1,延长HN至G,∠BMH和∠GND的角平分线相交于点E.
(1)、如图1,延长HN至G,∠BMH和∠GND的角平分线相交于点E.①若∠BME=25°,∠END=75°,则∠H的度数为 ▲ ;
②探究∠MEN与∠MHN的数量关系,并给予证明;
(2)、如图2,∠BMH和∠HND的角平分线相交于点E.作MP平分∠AMH,NQ∥MP交ME的延长线于点Q,若∠H=150°,求∠ENQ的度数.3. 如图 (1)、如图1,点E在BC上,∠A=∠D,∠ACB =∠CED.请说明 AB∥CD 的理由.(2)、如图2,AB∥CD,BG 平分∠ABE,与∠EDF 的平分线交于 H 点,若∠DEB比∠DHB 大60°,求∠DEB 的度数.(3)、保持(2)中所求的∠DEB 的度数不变,如图3,AB∥CD,BM 平分∠EBK,DN 平分∠CDE,作 BP∥DN,则∠PBM 的度数是否改变?若不变,请直接写出∠PBM 的度数;若改变,请说明理由.4. 如图,已知四边形ABCD是正方形,点E是AD边上的一点(不与点A,D重合),连接CE,以CE为一边作正方形CEFG,使点F,G与点A,B在CE的两侧,连接BE并延长,交GD延长线于点H.
(1)、如图1,点E在BC上,∠A=∠D,∠ACB =∠CED.请说明 AB∥CD 的理由.(2)、如图2,AB∥CD,BG 平分∠ABE,与∠EDF 的平分线交于 H 点,若∠DEB比∠DHB 大60°,求∠DEB 的度数.(3)、保持(2)中所求的∠DEB 的度数不变,如图3,AB∥CD,BM 平分∠EBK,DN 平分∠CDE,作 BP∥DN,则∠PBM 的度数是否改变?若不变,请直接写出∠PBM 的度数;若改变,请说明理由.4. 如图,已知四边形ABCD是正方形,点E是AD边上的一点(不与点A,D重合),连接CE,以CE为一边作正方形CEFG,使点F,G与点A,B在CE的两侧,连接BE并延长,交GD延长线于点H. (1)、如图1,请判断线段BE与GD的数量关系和位置关系,并说明理由;(2)、如图2,连接BG,若AB=2,CE= ,请你求出 的值.5. 如图1,E是直线AB、CD内部一点,AB∥CD,连接EA,ED.
(1)、如图1,请判断线段BE与GD的数量关系和位置关系,并说明理由;(2)、如图2,连接BG,若AB=2,CE= ,请你求出 的值.5. 如图1,E是直线AB、CD内部一点,AB∥CD,连接EA,ED. (1)、探究猜想:
(1)、探究猜想:①若∠A=20°,∠D=50°,则∠AED= ▲ 度;
②若∠A=35°,∠D=45°,则∠AED= ▲ 度;
③猜想图1中∠AED、∠EAB、∠EDC的数量关系并证明你的结论.
(2)、拓展应用:如图2,射线FE与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方),P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(直接写出结论,不要求证明)
6. 如图,AB∥CD,点E是AB上一点,连结CE. (1)、如图1,若CE平分∠ACD,过点E作EM⊥CE交CD于点M,试说明∠A=2∠CME;(2)、如图2,若AF平分∠CAB,CF平分∠DCE,且∠F=70°,求∠ACE的度数.(3)、如图3,过点E作EM⊥CE交∠DCE的平分线于点M,MN⊥CM交AB于点N,CH⊥AB,垂足为H.若∠ACH=∠ECH请直接写出∠MNB与∠A之间的数量关系.7. 如图,已知 , , .
(1)、如图1,若CE平分∠ACD,过点E作EM⊥CE交CD于点M,试说明∠A=2∠CME;(2)、如图2,若AF平分∠CAB,CF平分∠DCE,且∠F=70°,求∠ACE的度数.(3)、如图3,过点E作EM⊥CE交∠DCE的平分线于点M,MN⊥CM交AB于点N,CH⊥AB,垂足为H.若∠ACH=∠ECH请直接写出∠MNB与∠A之间的数量关系.7. 如图,已知 , , . (1)、求的度数;(2)、若平分 , 交于点 , 且 , 求的度数.8. 如图,已知直线射线 , .是射线上一动点,过点作交射线于点 , 连结.作 , 交直线于点 , 平分.
(1)、求的度数;(2)、若平分 , 交于点 , 且 , 求的度数.8. 如图,已知直线射线 , .是射线上一动点,过点作交射线于点 , 连结.作 , 交直线于点 , 平分. (1)、若点都在点的右侧.
(1)、若点都在点的右侧.①求的度数;
②若 , 求的度数.
(2)、在点的运动过程中,是否存在这样的情形,使 , 若存在,求出的度数;若不存在,请说明理由.9. 如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点D从点A开始,沿边AB向点B以每秒 个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0). (1)、当t=3时,求PD的长?(2)、当t为何值时,四边形BQPD的面积为△ABC面积的一半?(3)、是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.10. 如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)、当t=3时,求PD的长?(2)、当t为何值时,四边形BQPD的面积为△ABC面积的一半?(3)、是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.10. 如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题. (1)、探究1:王宣同学看到图后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌△EFC就行了,随即王宣同学写出了如下的证明过程:(2)、探究2:王宣同学继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论。(3)、探究3:王宣同学进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程,若不成立请你说明理由。11. 如图1,直线y= x+6分别交x轴,y轴于点A,点B,点C、P分别是线段OB,AB的中点,动点D,E分别在直线CP和线段AB上,设点E的横坐标为m,线段CD的长为n(n>0),且m+n=6,以DO,DE为邻边作▱ ODEF.
(1)、探究1:王宣同学看到图后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌△EFC就行了,随即王宣同学写出了如下的证明过程:(2)、探究2:王宣同学继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论。(3)、探究3:王宣同学进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程,若不成立请你说明理由。11. 如图1,直线y= x+6分别交x轴,y轴于点A,点B,点C、P分别是线段OB,AB的中点,动点D,E分别在直线CP和线段AB上,设点E的横坐标为m,线段CD的长为n(n>0),且m+n=6,以DO,DE为邻边作▱ ODEF. (1)、求点A和点P的坐标.(2)、如图2所示,当点D在点C左侧,且n=2时,求点F的坐标.(3)、当点F落在△AOB的边OB或AB上时,求点F的坐标.12. 如图,在平面直角坐标系中,点A,B的坐标分别是(﹣4,0),(0,8),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
(1)、求点A和点P的坐标.(2)、如图2所示,当点D在点C左侧,且n=2时,求点F的坐标.(3)、当点F落在△AOB的边OB或AB上时,求点F的坐标.12. 如图,在平面直角坐标系中,点A,B的坐标分别是(﹣4,0),(0,8),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.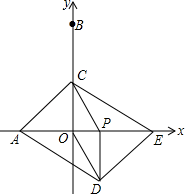 (1)、当点C运动到线段OB的中点时,求t的值及点E的坐标;(2)、当点C在线段OB上时,求证:四边形ADEC为平行四边形;(3)、在线段PE上取点F,使PF=3,过点F作MN⊥PE,截取FM= ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.13. 在平面直角坐标系中,已知点A(a,0),B(b,0),C(0,c),且+3|b﹣3|+2(c+2)2 =0.
(1)、当点C运动到线段OB的中点时,求t的值及点E的坐标;(2)、当点C在线段OB上时,求证:四边形ADEC为平行四边形;(3)、在线段PE上取点F,使PF=3,过点F作MN⊥PE,截取FM= ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.13. 在平面直角坐标系中,已知点A(a,0),B(b,0),C(0,c),且+3|b﹣3|+2(c+2)2 =0. (1)、直接写出S△ACB=;(2)、如图1,线段CB沿y轴正方向以每秒0.5个单位的速度匀速移动至DE(点C的对应点为D,点B的对应点为E),连接AD、OE.设运动时间为t秒,问:是否存在这样的t值,使得3S△ACD=2S△EOD?若存在,请求出t的值;若不存在,请说明理由.(3)、如图2,将线段AC往右平移3个单位长度至FG(点A的对应点为点F),线段FG与BC相交于点H. 若在x轴上存在点M使得S△MCH =2,试求出点M的坐标.14. 如图,正方形OABC中,O为坐标原点,点A、点C分别落在y轴、x轴上,点B坐标为(﹣4,4),点D为x轴上任意一点,将线段DA绕点D逆时针旋转90°,得对应线段为DE,作直线EC交y轴于点F.
(1)、直接写出S△ACB=;(2)、如图1,线段CB沿y轴正方向以每秒0.5个单位的速度匀速移动至DE(点C的对应点为D,点B的对应点为E),连接AD、OE.设运动时间为t秒,问:是否存在这样的t值,使得3S△ACD=2S△EOD?若存在,请求出t的值;若不存在,请说明理由.(3)、如图2,将线段AC往右平移3个单位长度至FG(点A的对应点为点F),线段FG与BC相交于点H. 若在x轴上存在点M使得S△MCH =2,试求出点M的坐标.14. 如图,正方形OABC中,O为坐标原点,点A、点C分别落在y轴、x轴上,点B坐标为(﹣4,4),点D为x轴上任意一点,将线段DA绕点D逆时针旋转90°,得对应线段为DE,作直线EC交y轴于点F. (1)、如图(1),当点D为OC的中点时,求点E的坐标;(2)、如图(2),当点D在边OC上任意移动时,猜想:点F的位置是否发生变化?若不变,求出点F的坐标,若改变,请说明理由;(3)、如图(3),当点D在x轴的正半轴上移动时,请在图(3)画出图形(不保留作图痕迹),并直接回答点F的位置与(2)中猜想的结论是否一致.
(1)、如图(1),当点D为OC的中点时,求点E的坐标;(2)、如图(2),当点D在边OC上任意移动时,猜想:点F的位置是否发生变化?若不变,求出点F的坐标,若改变,请说明理由;(3)、如图(3),当点D在x轴的正半轴上移动时,请在图(3)画出图形(不保留作图痕迹),并直接回答点F的位置与(2)中猜想的结论是否一致.答:_(填“一致”或“不一致”).
15. 如图,在平面直角坐标系中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点. (1)、用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)、若四边形PQOB的面积是 , 且 , 试求点P的坐标,并求出直线PA与PB的函数表达式;(3)、在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.16. 项目化学习:车轮的形状.
(1)、用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)、若四边形PQOB的面积是 , 且 , 试求点P的坐标,并求出直线PA与PB的函数表达式;(3)、在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.16. 项目化学习:车轮的形状.【问题提出】车轮为什么要做成圆形, 这里面有什么数学原理?
(1)、【合作探究】

探究 组:如图1,圆形车轮半径为 ,其车轮轴心 到地面的距离始终为 .
探究 组:如图2,正方形车轮的轴心为 ,若正方形的边长为 ,求车轮轴心 最高点与最低点的高度差.
探究 组:如图3, 有一个破损的圆形车轮, 半径为 ,破损部分是一个弓形,其所对圆心角为 ,其车轮轴心为 ,让车轮在地上无滑动地滚动一周,求点 经过的路程.探究发现:车辆的平稳关键看车轮轴心是否稳定.
(2)、【拓展延伸】如图4,分别以正三角形的三个顶点 为圆心,以正三角形的边长为半径作 圆弧,这个曲线图形叫做“莱洛三角形”.
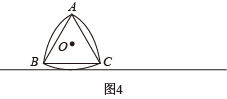
探究 组:使 “莱洛三角形” 沿水平方向向右滚动,在滚动过程中,其每时每刻都有 “最高点”,“中心点” 也在不断移动位置,那么在 “莱洛三角形” 滚动一周的过程中,其“最高点”和“中心点”所形成的图案大致是 .
延伸发现:“莱洛三角形”在滚动时始终位于一组平行线之间,因此放在其上的物体也能够保持平衡,但其车轴中心 并不稳定.
17. 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=12cm,AD=15cm,BC=20cm,动点E从点A出发,在线段AD上以每秒1cm的速度向点D运动,动点F从点C出发,在线段CB上以每秒2cm的速度运动到B点返回,点E、F分别从点A、C同时出发,当点E运动到点D时,点F随之停止运动,设运动的时间为t(秒).
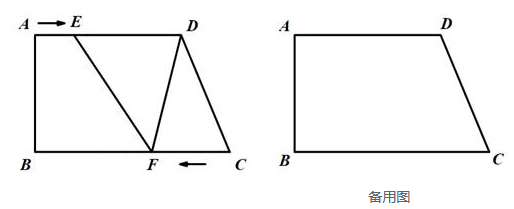 (1)、用含t的代数式表示DE,DE=;(2)、若四边形EFCD是平行四边形,求此时t的值;(3)、是否存在点F,使△FCD是等腰三角形?若存在,请直接写出所有满足要求的t的值;若不存在,请说明理由.18. 问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连接AF,BE.
(1)、用含t的代数式表示DE,DE=;(2)、若四边形EFCD是平行四边形,求此时t的值;(3)、是否存在点F,使△FCD是等腰三角形?若存在,请直接写出所有满足要求的t的值;若不存在,请说明理由.18. 问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连接AF,BE. (1)、特例探究:如图1,若△ADE和△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;(2)、拓展应用:如图2,在△ADE和△DCF中, , , 且 , 求四边形ABFE的面积?19. 如图,⊙O的直径AB垂直于弦CD于点E, , ,点P是CD延长线上异于点D的一个动点,连结AP交⊙O于点Q,连结CQ交AB于点F,则点F的位置随着点P位置的改变而改变.
(1)、特例探究:如图1,若△ADE和△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;(2)、拓展应用:如图2,在△ADE和△DCF中, , , 且 , 求四边形ABFE的面积?19. 如图,⊙O的直径AB垂直于弦CD于点E, , ,点P是CD延长线上异于点D的一个动点,连结AP交⊙O于点Q,连结CQ交AB于点F,则点F的位置随着点P位置的改变而改变.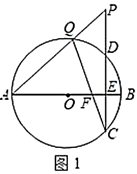
 (1)、如图1,当 时,求 的值;(2)、如图2,连结AC,DQ,在点P运动过程中,设 , .
(1)、如图1,当 时,求 的值;(2)、如图2,连结AC,DQ,在点P运动过程中,设 , .①求证: ;
②求y与x之间的函数关系式.
20. 如图1,四边形 是 的内接四边形,其中 ,对角线 相交于点 ,在 上取一点 ,使得 ,过点 作 交 于点 .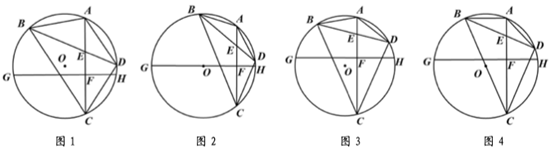 (1)、证明: ;(2)、如图 2,若 ,且 恰好经过圆心 ,求 的值;(3)、若 ,设 的长为 .
(1)、证明: ;(2)、如图 2,若 ,且 恰好经过圆心 ,求 的值;(3)、若 ,设 的长为 .①如图3,用含有 的代数式表示 的周长;
②如图4, 恰好经过圆心 ,求 内切圆半径与外接圆半径的比值.
21. 四边形为的内接四边形, . (1)、如图1,求证:;(2)、如图2,为的直径,连接 , 过点O作的垂线,点F为垂足,求证:;(3)、如图3,在(2)的条件下,过点O作的垂线,点G为垂足,若 , , , 求的长.22. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.
(1)、如图1,求证:;(2)、如图2,为的直径,连接 , 过点O作的垂线,点F为垂足,求证:;(3)、如图3,在(2)的条件下,过点O作的垂线,点G为垂足,若 , , , 求的长.22. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.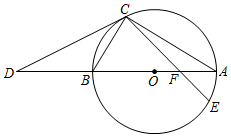 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为 , △ABC的面积为 , 求CD的长;(3)、在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若 , 求BF的长.23. 如图,⊙O是的外接圆,圆心O在AC上.过点B作直线交AC的延长线于点D,使得 . 过点A作于点E,交⊙O于点F.
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为 , △ABC的面积为 , 求CD的长;(3)、在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若 , 求BF的长.23. 如图,⊙O是的外接圆,圆心O在AC上.过点B作直线交AC的延长线于点D,使得 . 过点A作于点E,交⊙O于点F. (1)、求证:BD是⊙O的切线;(2)、若 , , 则AE的长为 .24. 已知AB为直径,△PCD是内接三角形, .
(1)、求证:BD是⊙O的切线;(2)、若 , , 则AE的长为 .24. 已知AB为直径,△PCD是内接三角形, . (1)、如图1,求的度数;(2)、如图2,PD交AB于点M,作交AB于点E,连接CO并延长交PD于点N,若CP平分 , 求证:;(3)、如图3,在(2)的条件下,F是外一点,FC是的切线,FD∥PC,若 , , 求PD的长.25. 在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连接BE 交CD于点N,点P在CD的延长线上,连接PE,PN=PE:
(1)、如图1,求的度数;(2)、如图2,PD交AB于点M,作交AB于点E,连接CO并延长交PD于点N,若CP平分 , 求证:;(3)、如图3,在(2)的条件下,F是外一点,FC是的切线,FD∥PC,若 , , 求PD的长.25. 在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连接BE 交CD于点N,点P在CD的延长线上,连接PE,PN=PE: (1)、求证:PE是⊙O的切线:(2)、连接DE,若DE//AB,OF=3,BF=2,求PN的长。26. △ABC是⊙O的内接三角形,点P是⊙O上一点,且点P与点A在BC的两侧,连接PA,PB,PC.
(1)、求证:PE是⊙O的切线:(2)、连接DE,若DE//AB,OF=3,BF=2,求PN的长。26. △ABC是⊙O的内接三角形,点P是⊙O上一点,且点P与点A在BC的两侧,连接PA,PB,PC. (1)、如图①,若△ABC是等边三角形,则线段PA,PB,PC之间有怎样的数量关系,并证明你的结论.(2)、如图②,把(1)中的△ABC改为等腰直角三角形,∠BAC=90°,其他条件不变,三条线段PA,PB,PC还有以上的数量关系吗?说明理由.(3)、如图③,把(1)中△ABC改为任意三角形,AB=c,AC=b,BC=a时,其他条件不变,则PA,PB,PC三条线段的数量关系为(直接写结果)(4)、由以上你能发现圆内接四边形的四条边和对角线有什么关系?27. 如图,是四边形的外接圆,是的直径, , 交的延长线于点E,平分 .
(1)、如图①,若△ABC是等边三角形,则线段PA,PB,PC之间有怎样的数量关系,并证明你的结论.(2)、如图②,把(1)中的△ABC改为等腰直角三角形,∠BAC=90°,其他条件不变,三条线段PA,PB,PC还有以上的数量关系吗?说明理由.(3)、如图③,把(1)中△ABC改为任意三角形,AB=c,AC=b,BC=a时,其他条件不变,则PA,PB,PC三条线段的数量关系为(直接写结果)(4)、由以上你能发现圆内接四边形的四条边和对角线有什么关系?27. 如图,是四边形的外接圆,是的直径, , 交的延长线于点E,平分 .\
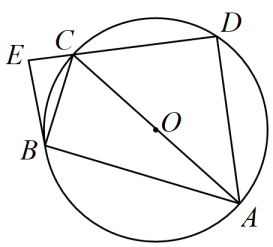 (1)、求证:是的切线;(2)、若 , , 求的长.28. 已知,如图1,Rt△ABC中,AB=AC,∠BAC=90°,D为△ABC外一点,且∠ADC=90°,E为BC中点,AF∥BC,连接EF交AD于点G,且EF⊥ED交AC于点H,AF=1.
(1)、求证:是的切线;(2)、若 , , 求的长.28. 已知,如图1,Rt△ABC中,AB=AC,∠BAC=90°,D为△ABC外一点,且∠ADC=90°,E为BC中点,AF∥BC,连接EF交AD于点G,且EF⊥ED交AC于点H,AF=1. (1)、若 , 求EF的长;(2)、在(1)的条件下,求CD的值;(3)、如图2,连接BD,BG,若BD=AC,求证:BG⊥AD.29. 如图,在小学我们通过观察、实验的方法得到了“三角形内角和是180°”的结论。小明通过这学期的学习知道:由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的符合题意性.
(1)、若 , 求EF的长;(2)、在(1)的条件下,求CD的值;(3)、如图2,连接BD,BG,若BD=AC,求证:BG⊥AD.29. 如图,在小学我们通过观察、实验的方法得到了“三角形内角和是180°”的结论。小明通过这学期的学习知道:由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的符合题意性.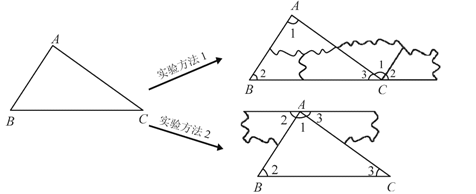
受到实验方法1的启发,小明形成了证明该结论的想法:实验1的拼接方法直观上看,是把和移动到的右侧,且使这三个角的顶点重合,如果把这种拼接方法抽象为几何图形,那么利用平行线的性质就可以解决问题了.
小明的证明过程如下:
已知:如图, . 求证: .

证明:延长 , 过点作 .
∴ ▲ (两直线平行,内错角相等),
( ▲ ).
∵(平角定义),
∴ .
(1)、请你补充完善小明方法1的证明过程;(2)、请你参考小明解决问题的方法1的思路,自行画图标注好顶点字母,写出方法2证明该结论的过程.30. 已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论. (1)、如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: ;(2)、如图2,AB∥EF,BC∥DE.∠1与∠2的关系是:;(3)、经过上述证明,我们可以得到一个真命题:如果 , 那么 .
(1)、如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: ;(2)、如图2,AB∥EF,BC∥DE.∠1与∠2的关系是:;(3)、经过上述证明,我们可以得到一个真命题:如果 , 那么 .