备考浙教版中考数学题型专项训练 图形的性质填空题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、填空题
-
1. 如图,一位跑酷运动员准备以连续两次“跳跃”结束一次跑酷表演,即在水平面 AB 上跑至 B点,向上跃起至最高点 P,然后落在点 C 处,继续在水平面 CD 上跃起落在点 D,若∠ABK 和∠KCD 的平分线的反向延长线刚好交于最高点 P,∠BKC=88°,则∠P=度.
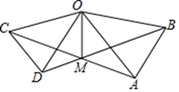
 2. 一副三角板按如图所示叠放在一起,∠C=60°,∠OAB=45°,其中点B,D重合,若固定△AOB,将三角板ACD绕着公共顶点A顺时针旋转一周后停止,当旋转的角度为时,CD∥AO.
2. 一副三角板按如图所示叠放在一起,∠C=60°,∠OAB=45°,其中点B,D重合,若固定△AOB,将三角板ACD绕着公共顶点A顺时针旋转一周后停止,当旋转的角度为时,CD∥AO. 3. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)
3. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)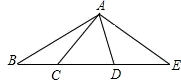 4. 如图在矩形ABCD中,AB=6,AD=8,E为对角线AC上的动点,EF⊥DE交BC边于点F,以DE,EF为邻边作矩形DEFG.
4. 如图在矩形ABCD中,AB=6,AD=8,E为对角线AC上的动点,EF⊥DE交BC边于点F,以DE,EF为邻边作矩形DEFG. (1)、当AE=2时,求;(2)、点H在AD上且HD=3,连接HG,则HG的取值范围是.5. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 , 椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm.
(1)、当AE=2时,求;(2)、点H在AD上且HD=3,连接HG,则HG的取值范围是.5. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 , 椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm. (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为cm(结果精确到0.1cm).6. 将一条两边互相平行的纸带沿EF折叠,如图1,AD∥BC,ED′∥FC′,设∠AED′ = x°.
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为cm(结果精确到0.1cm).6. 将一条两边互相平行的纸带沿EF折叠,如图1,AD∥BC,ED′∥FC′,设∠AED′ = x°. (1)、∠EFB = ;(用含x的代数式表示)(2)、若将图1继续沿BF折叠成图2,∠EFC'' = .(用含x的代数式表示)7. 如图消防云梯,其示意图如图1所示,其由救援台 、延展臂 在 的左侧)、伸展主臂 、支撑臂 构成,在作业过程中,救援台 、车身 及地面 三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2.使得延展臂 与支摚臂 所在直线互相垂直,且 ,则这时展角 .
(1)、∠EFB = ;(用含x的代数式表示)(2)、若将图1继续沿BF折叠成图2,∠EFC'' = .(用含x的代数式表示)7. 如图消防云梯,其示意图如图1所示,其由救援台 、延展臂 在 的左侧)、伸展主臂 、支撑臂 构成,在作业过程中,救援台 、车身 及地面 三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2.使得延展臂 与支摚臂 所在直线互相垂直,且 ,则这时展角 . 8. 正方形中, , E为AB的中点,将沿折叠得到 , , 垂足为 , 则.
8. 正方形中, , E为AB的中点,将沿折叠得到 , , 垂足为 , 则. 9. 如图,在▱ ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则▱ ABCD的周长为 .
9. 如图,在▱ ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则▱ ABCD的周长为 . 10. 如图,△ABC中,∠B=30°,∠ACB=90°,AB=2,D在BC上,将线段AD绕点A逆时针旋转60°得AP,则CP的最小值为.
10. 如图,△ABC中,∠B=30°,∠ACB=90°,AB=2,D在BC上,将线段AD绕点A逆时针旋转60°得AP,则CP的最小值为.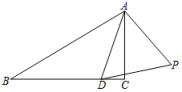 11. 如图,矩形ABCD, .点E是AB的中点,将 沿DE折叠,点A落在矩形内点F处,连结BF,CF.若 的面积为37.5,则 的面积为 .
11. 如图,矩形ABCD, .点E是AB的中点,将 沿DE折叠,点A落在矩形内点F处,连结BF,CF.若 的面积为37.5,则 的面积为 .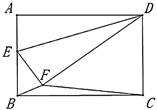 12. 如图,在平行四边形ABCD中,BC=6,∠ABC=60°,BE平分∠ABC,点F为BC上一点,点G为BE上一点,连接CG,FG,则CG FG的最小值为 .
12. 如图,在平行四边形ABCD中,BC=6,∠ABC=60°,BE平分∠ABC,点F为BC上一点,点G为BE上一点,连接CG,FG,则CG FG的最小值为 .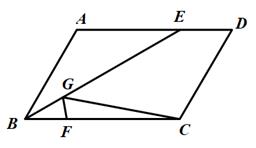 13. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,若AD=4,则图中阴影部分的面积为
13. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,若AD=4,则图中阴影部分的面积为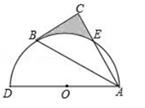 14. 已知O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .15. 如图,在正方形ABCD中,M是对角线BD上一点,连接AM,将AM绕点A逆时针旋转90°得AN,连接MN交AD于E点,连接DN.则下列结论中:①;②;③;④当时,则 . 其中正确结论的序号是 .
14. 已知O、A、B的坐标分别是(0,0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .15. 如图,在正方形ABCD中,M是对角线BD上一点,连接AM,将AM绕点A逆时针旋转90°得AN,连接MN交AD于E点,连接DN.则下列结论中:①;②;③;④当时,则 . 其中正确结论的序号是 .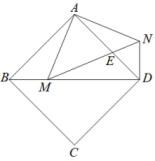 16. 如图,正方形中,A,C分别在x,y轴正半轴上,反比例函数的图象与边 , 分别交于点D,E,且 , 对角线把分成面积相等的两部分,则 .
16. 如图,正方形中,A,C分别在x,y轴正半轴上,反比例函数的图象与边 , 分别交于点D,E,且 , 对角线把分成面积相等的两部分,则 . 17. 如图①,在菱形ABCD中,点E为BC的中点,点F为AD上一动点.将四边形FECD沿着EF翻折,得到四边形FEC'D',C'E与AB交于点P
17. 如图①,在菱形ABCD中,点E为BC的中点,点F为AD上一动点.将四边形FECD沿着EF翻折,得到四边形FEC'D',C'E与AB交于点P (1)、如图①,若点F与点A重合时,恰有FP=FE,则= .(2)、在(1)问的结论下,如图② ,当AF平分∠EFD'时,的值为 .18. 如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,D是BC边上一点,线段DA绕点D顺时针旋转90°得到DE,连结AE,若F是AE的中点,则CF的最小值为 .
(1)、如图①,若点F与点A重合时,恰有FP=FE,则= .(2)、在(1)问的结论下,如图② ,当AF平分∠EFD'时,的值为 .18. 如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,D是BC边上一点,线段DA绕点D顺时针旋转90°得到DE,连结AE,若F是AE的中点,则CF的最小值为 . 19. 如图,在 中, 为 延长线上一点,连接 ,则 的最大值是 .
19. 如图,在 中, 为 延长线上一点,连接 ,则 的最大值是 .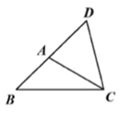 20. 如图,在四边形中, , , , 点在对角线上运动,为的外接圆,当与四边形的一边相切时,其半径为.
20. 如图,在四边形中, , , , 点在对角线上运动,为的外接圆,当与四边形的一边相切时,其半径为. 21. 如图,等边△ABC的边长为6,三角形内部有一个半径为1的 , 若含与△ABC边相切的情况,则点P可移动的最大范围(最大面积)是 .
21. 如图,等边△ABC的边长为6,三角形内部有一个半径为1的 , 若含与△ABC边相切的情况,则点P可移动的最大范围(最大面积)是 . 22. 如图,草坪边上有两条相互垂直的小路 m,n,垂足为 O,在草坪内有一个圆形花坛,花坛边缘上有A, B,C 三棵小树,为了估测圆形花坛的半径,在小路上 D,E,F 三点观测,发现均有两棵树与观测点在同一直线上,从观测点 E 沿着 ED 方向走 5 米到 G 点.测得∠BGD=45°,OF=18 米,∠AFO=90°,tan∠BDE=tan∠BED= , 则树 B 到小路 m 的距离为米,圆形花坛的半径长为米.
22. 如图,草坪边上有两条相互垂直的小路 m,n,垂足为 O,在草坪内有一个圆形花坛,花坛边缘上有A, B,C 三棵小树,为了估测圆形花坛的半径,在小路上 D,E,F 三点观测,发现均有两棵树与观测点在同一直线上,从观测点 E 沿着 ED 方向走 5 米到 G 点.测得∠BGD=45°,OF=18 米,∠AFO=90°,tan∠BDE=tan∠BED= , 则树 B 到小路 m 的距离为米,圆形花坛的半径长为米. 23. 如图,AB是半径为4的的弦,且AB=6,将AB沿着弦AB折叠,点C是折叠后的上一动点,连接并延长BC交于点D,点E是CD的中点,连接EO.则EO的最小值为.
23. 如图,AB是半径为4的的弦,且AB=6,将AB沿着弦AB折叠,点C是折叠后的上一动点,连接并延长BC交于点D,点E是CD的中点,连接EO.则EO的最小值为. 24. 如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为.
24. 如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为. 25. 如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是 . (写出所有正确结论的序号)
25. 如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是 . (写出所有正确结论的序号)①PB=PD;②的长为;③∠DBE=45°;④△BCF∽△PFB;⑤为定值.
 26. 如图,点在以为直径的半圆上, , , 点在线段上运动,点与点关于对称,于点 , 并交的延长线与点 . 下列结论:①;②;③线段的最小值为;④当时,与半圆相切;⑤当点从点运动到点时,线段扫过的面积是 . 其中正确的结论的序号为 .
26. 如图,点在以为直径的半圆上, , , 点在线段上运动,点与点关于对称,于点 , 并交的延长线与点 . 下列结论:①;②;③线段的最小值为;④当时,与半圆相切;⑤当点从点运动到点时,线段扫过的面积是 . 其中正确的结论的序号为 .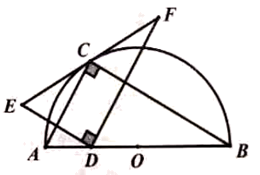 27. 如图,墙上有一个矩形门洞ABCD,现要将其改为直径为4m的圆弧形,圆弧经过点B,C分别交AB,CD于E,F.若m,m,则要打掉的墙体面积为.
27. 如图,墙上有一个矩形门洞ABCD,现要将其改为直径为4m的圆弧形,圆弧经过点B,C分别交AB,CD于E,F.若m,m,则要打掉的墙体面积为. 28. 《算法统宗》是我国明代数学著作,它记载了多位数相乘的方法,如图1给出了34×25=850的步骤:①将34,25分别写在方格的上边和右边;②把上述各数字乘积的十位(不足写0)与个位分别填入小方格中斜线两侧;③沿斜线方向将数字相加,记录在方格左边和下边;④将所得数字从左上到右下依次排列(满十进一).若图2中a,b,c,d均为正整数,且c,d都不大于8,则b的值为 , 该图表示的乘积结果为 .
28. 《算法统宗》是我国明代数学著作,它记载了多位数相乘的方法,如图1给出了34×25=850的步骤:①将34,25分别写在方格的上边和右边;②把上述各数字乘积的十位(不足写0)与个位分别填入小方格中斜线两侧;③沿斜线方向将数字相加,记录在方格左边和下边;④将所得数字从左上到右下依次排列(满十进一).若图2中a,b,c,d均为正整数,且c,d都不大于8,则b的值为 , 该图表示的乘积结果为 . 29. 如图,在矩形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME=15°,则∠ABE=
29. 如图,在矩形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME=15°,则∠ABE= 30. 如图,正方形 的边长为6,点 、 分别在 、 上,点 为 的中点.将 , 分别沿 , 向内折叠,此时 与 重合( 、 都落在点 ),连接 .则下列结论正确的有(直接写序号即可)
30. 如图,正方形 的边长为6,点 、 分别在 、 上,点 为 的中点.将 , 分别沿 , 向内折叠,此时 与 重合( 、 都落在点 ),连接 .则下列结论正确的有(直接写序号即可)① ;② ;③三角形 是等边三角形; ④三角形 的面积为30.
 31. 以下四个命题:①用换元法解分式方程+=1时,如果设=y,那么可以将原方程化为关于y的整式方程y2+y-2=0;②二次函数y=ax2-2ax+1,自变量的两个值x1 , x2对应的函数值分别为y1、y2 , 若|x1-1|>|x2-1|,则a(y1-y2)>0;③有一个圆锥,与底面圆直径是且体积为的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为;④如果半径为r的圆的内接正五边形的边长为a,那么a=2r sin54°.其中正确的命题的序号为
31. 以下四个命题:①用换元法解分式方程+=1时,如果设=y,那么可以将原方程化为关于y的整式方程y2+y-2=0;②二次函数y=ax2-2ax+1,自变量的两个值x1 , x2对应的函数值分别为y1、y2 , 若|x1-1|>|x2-1|,则a(y1-y2)>0;③有一个圆锥,与底面圆直径是且体积为的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为;④如果半径为r的圆的内接正五边形的边长为a,那么a=2r sin54°.其中正确的命题的序号为